例4-9 判断一个数是否为素数。
分析:素数又称为质数,就是除了能被1和它本身整除之外,不能被其他自然数整除的自然数。例如,自然数“num=36”,如果要测试这个数是否为素数,从定义出发,就应对2∽35之间的数进行测试。但是,可以发现“36%2==0”时,也就意味着“36%18==0”,因此得到两个约数。对于36,这样的约数很多,如(2,18),(3,12),(4,9),(6,6),(9,4),(12,3),(18,2)。当找到(6,6)后,以后的约数就都重复了。从这个例子可以看出,循环大可不必运行到“num-1”,而是将循环的次数控制到 就行。
#include <stdio.h>
#include <math.h>
main( )
{ int num, j, tag=1, m;
printf( "请输入一个自然数:" );
scanf( "%d", &num );
m=sqrt( num );
for( j = 2; j <= m; j++ )
if( num % j == 0) // num 被 j 整除
{ tag=0;
break;
}
if( tag == 1)
printf("%d 是素数\n",num);
else
printf("%d 不是素数\n",num);
}
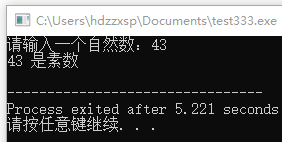
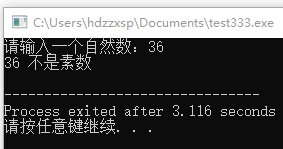
运行结果如图4-13所示。
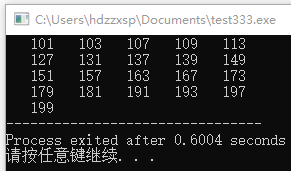
例4-10 找出100∽200之间的所有素数
分析:
#include <stdio.h>
#include <math.h>
main( )
{ int num, j, tag, m, cnt=0;
for( num = 101; num < 200; num += 2)
{
tag = 1;
m = sqrt( num );
for( j = 2; j <= m; j++ )
if( num % j == 0)
{ tag = 0; break; }
if( tag == 1 )
{
printf(" %5d", num);
cnt ++;
if( cnt % 5 == 0)
printf("\n");
}
}
}
例4-11 输入两个整数,求它们的最大公约数。方法是采用”辗转相除法“,即反复模除取余,直到余数为 0。
#include <stdio.h>
#include <conio.h>
main( )
{ int a, b, r, tmp;
printf(" 输入两个整数:");
scanf("%d %d", &a, &b);
if( a<b)
{ tmp = a; a = b; b = tmp; }
do
{
r = a % b;
a = b;
b = r;
} while( r );
printf("最大公约数为:%d\n", a);
getch( );
}
| 变量名 | r | a | b | 变量名 | r | a | b |
|---|---|---|---|---|---|---|---|
| 初始状态 | 125 | 75 | 第 2 轮循环 | 25 | 50 | 25 | |
| 第 1 轮循环 | 50 | 75 | 50 | 第 3 轮循环 | 0 | 25 | 0 |
例4-12 “百鸡问题”是我国古代数学家张丘建在他编写的《算经》里提出的一个不定方程问题,即“鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡。问鸡翁、母、雏各几何?”
分析:设公鸡(鸡翁)、母鸡(鸡母)和小鸡(鸡雏)各为x、y和z只。因为总共100钱,若全部买公鸡,最多买20只,显然x的变化范围在0~20之间。同理,y的变化范围在0~33间。所得到的不定方程应为:
(1) x+y+z=100 方程1
(2) 5x+3y+z/3=100 方程2
计算程序为:
#include <stdio.h>
main( )
{ int x, y, z;
for( x = 0; x <= 20 ; ++x)
for( y = 0; y <= 33; ++y)
{
z=100-x-y; // 由方程1得知
if(( z % 3 == 0) && ( 5*x+3*y+z/3 ==100 )) // 由方程2得知
printf("公鸡:%-2d 母鸡:%-2d 小鸡:%-2d\n", x, y, z);
}
}
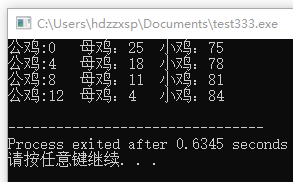
因为这是一个不定方程组,所以可能有多组解。程序运行的输出结果如图4-16所示。
图4-16 例4-12运行结果