直线的投影 SECTION TWO PROJECTION OF  LINES

一、直线的投影图与直观图的画法 Projection and pictorial drawing of lines

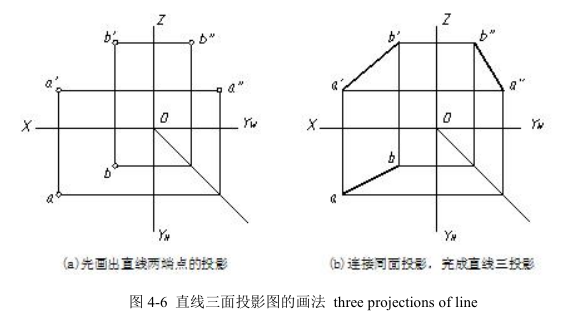
       直线的投影一般仍为直线。画直线段的投影，可先画出直线段两端点的投影，然后用粗实线将其同面投影连成直线即得，如图 4-6 所示。

        The projection of lines will produce lines and not any other from of shape.That is when you project lines you will get lines. The result of projection is a line connecting the projected points of two ends of line segments. As shown in fig 4-6.

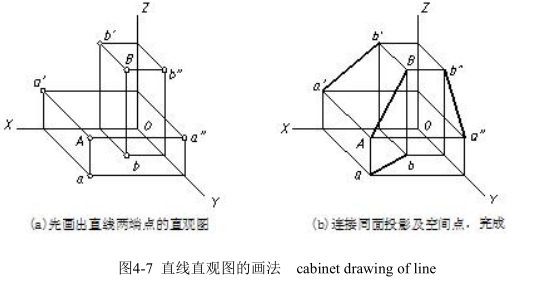
      画直线的直观图时，可先画出直线上两点的直观图，然后用粗实线分别连接两点的同面投影和空间两点即得，如图 4-7 所示。

      Pictorial drawing of lines 

      Firstly, finish the pictorial drawing of points, and then connect the two points in space with thick continuous line.as shown in fig 4-7.

二、各种位置直线的投影特性 Characteristics of line projection

      在三面投影体系中，直线的位置分为三类：一般位置直线、投影面平行线、投影面垂直线。后两类统称为特殊位置直线。

      According to the analysis of the basic characteristics of orthographic projection, one knows that the projected line has three relative positions with respect to the projection planes. This leads to three classes and seven cases of relative positions in three-view projection system.

1.一般位置直线 Aline in general position

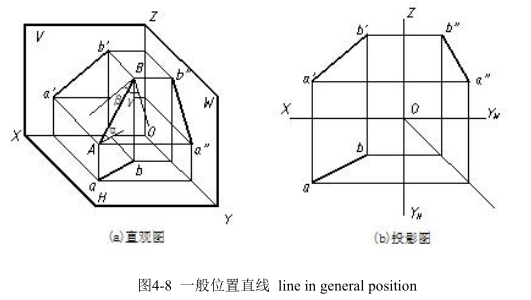
      相对三投影面都倾斜的直线称为一般位置直线，直线与 H、V、W 三投影面的倾角分别用α、β、γ表示，如图 4-8 所示。

      一般位置直线的投影特性为：三投影均为斜线且小于实长，三投影与投影轴的夹角不反映空间直线与投影面的倾角。

      In this case, the line being projected is oblique with the three projection planes. The three projections are all oblique lines with the projection axis and shorter than true length of line and as shown in fig 4-8.

2.投影面平行线 line parallel to projection planes

      平行一个投影面，倾斜于另外两个投影面的直线称为投影面平行线。投影面平行线分为三种：

      正平线 —— 平行于 V 面，倾斜于 H、W 面；

      水平线 —— 平行于 H 面，倾斜于 V、W 面；

      侧平线 —— 平行于 W 面，倾斜于 V、H 面。

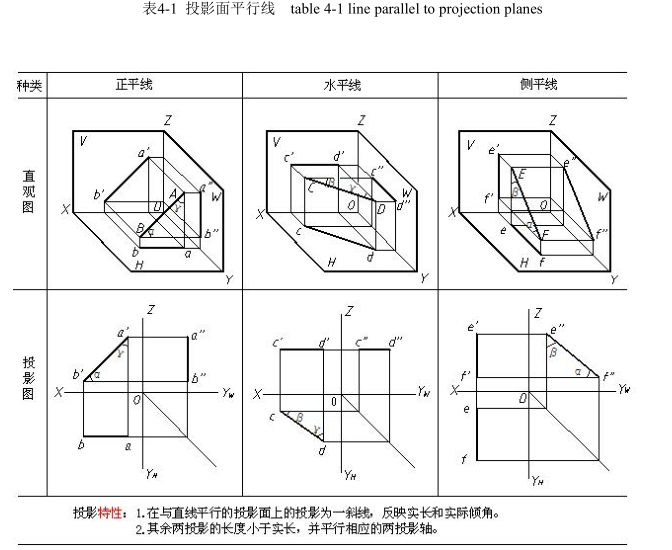
      各种投影面平行线的直观图、三投影图及投影特性见表 4-1。

      Position: let the line be parallel one projection plane and incline to the other two projection planes.

      Projection: one oblique line and two lines. The oblique line shows the true length of line in space.

      The two lines are shorter than the true length.

      Types: horizontal line (the line parallels the HP and inclines on the other projection planes. The projection in the HP is oblique line and represents the true length of line in space)

      Frontal line: (the line parallels the VP and inclines on the other projection planes. The projection in the HP is oblique line and represents the true length of line in space)

      Profile line: (the line parallels the AVP and inclines on the other projection planes. The projection in the HP is oblique line and represents the true length of line in space).

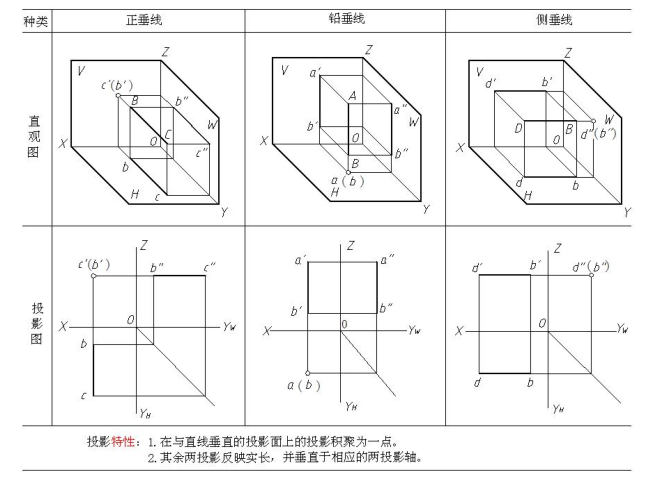
3.投影面垂直线 perpendicular line to projection planes

       垂直一个投影面，平行于另外两个投影面的直线称为投影面垂直线。投影面垂直线也可分为三种：

       正垂线 —— 垂直于 V 面，平行于 H、W 面；

       铅垂线 —— 垂直于 H 面，平行于 V、W 面；

       侧垂线 —— 垂直于 W 面，平行于 V、H 面。

       各种投影面垂直线的直观图、三投影图及投影特性见表 4-2。

       Position: if the line is perpendicular to one projection plane, it must be parallel the other two projection planes.

       Projection: one point and two line. The two lines both reflect the true length of line in space. The point shows the accumulated projection.

       H-perpendicular line: the line is perpendicular to HP and parallels the other two projection planes.

       V-perpendicular line: the line is perpendicular to VP and parallels the other two projection planes.

       W-perpendicular line: the line is perpendicular to AVP and parallels the other two projection planes.

                                    表 4-2 投影面垂直线 Lines perpendicular to a projection plane

       比较三类直线的投影特性可以看出：

       直线只要有两个投影倾斜于投影轴，即为一般位置直线；直线只有一个投影为斜线，即为投影面的平行线；直线的一个投影积聚为点，即为投影面的垂直线。

三、直线上点的从属性 Subordination of point on the line

       点在直线上，点的各面投影必在该直线的同面投影上，这个特性称为从属性。反之，点的各面投影只要有一个不在直线的同面投影上，则点就一定不在该直线上。

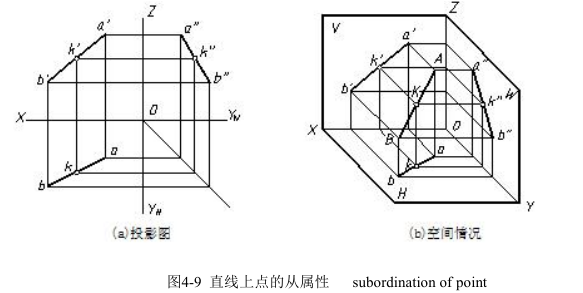
       如图 4-9(a)所示，K 点的三面投影 k、k′、k″分别在直线 AB 的同面投影 a b、a′b′、a″b″上，并且三投影间符合点的投影规律，由此可判定 K 点必在直线 AB 上，如图 4-9(b)所示。

       If one point is on the line in space, the projections of point must be in the projection of line. Otherwise, one of three is not on the projection of line, it can be determined that the point is not on the line in space. With the use of the principle, one can judge the point whether it is on the line or not.

四、两直线的相对位置 Relative position of two lines

       两直线的相对位置有平行、相交、交叉三种情况，前两种位置直线统称为同面直线，后一种称为异面直线。

       There are three kinds of relative positions of two lines. In the same plane, they may parallel each other, and they probably intersect. The third kind is the two lines can not be in any same plane.

1.两直线平行

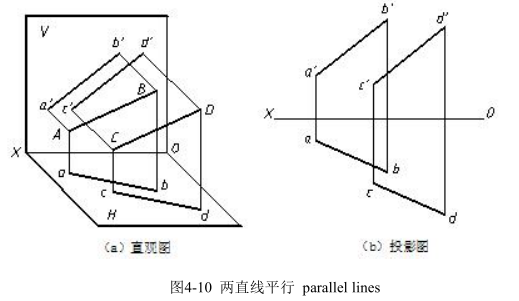
       如图 4-10 所示，AB∥CD，直线与投射线形成的平面 ABba∥CDdc，它们与水平投影面的交线互相平行，即 ab∥cd。同理可证明 a′b′∥c′d′、a″b″∥c″d″。

       由此可得平行两直线的投影特性：空间两直线平行，它们的同面投影必定相互平行。反之，各组同面投影都互相平行，两直线在空间必然互相平行。

       Parallel line: if two lines are parallel in space, the projections of them must parallel. On the contrary, if the projections are parallel to each other, one can decide the two lines are parallel in space. One notes that if the two lines are general lines, he can judge whether they parallel or not based two projections of lines.

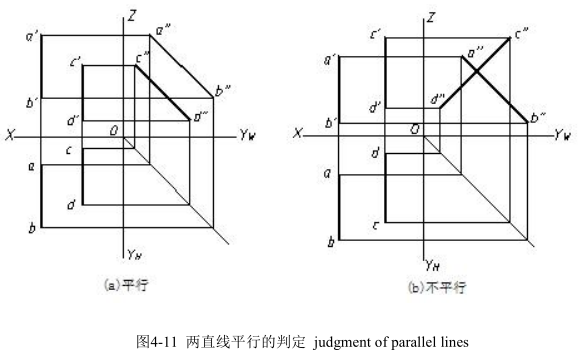
       当两直线是一般位置时，只要有两对同面投影互相平行就可判定两直线在空间平行。

       若两直线在空间同时平行某投影面，判定两直线是否平行的关键点，是要看它们在所平行的投影面上的投影是否平行，投影平行在空间才平行，如图 4-11 所示。

2.两直线相交

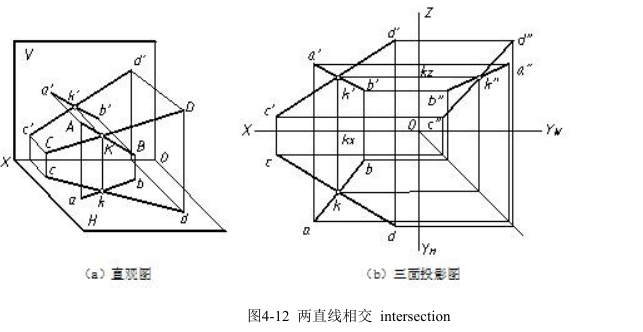
       相交两直线必有一交点，交点为两直线的共有点。如图 4-12 所示，AB 与 CD 交于K 点，K 点的三投影必符合点的投影规律，即 k′k ⊥ OX，k′k″⊥OZ，k kx = k″kz；K点在 AB 上，k′应在 a′b′上，k 在 a b 上，k″在 a″b″上；K 点在 CD 上，k′应在 c′d′上，k在 cd 上，k″在 c″d″上。

       由此可得相交两直线的投影特性：若空间两直线相交，它们的同面投影必定相交，并且交点的投影符合点的投影规律。反之，两直线的各组同面投影都相交，而且交点符合空间点的投影规律，这两直线在空间一定相交。

       Intersect line: if two lines intersect one point, the projection of point must be in line with the projection rules. If two lines intersect in space, the projection in the same projection plane of line must intersect one point. On the contrary, if all projections in the same projection plane intersect one point and the projection of point is in accordance with the projection rules, the two lines are sure to intersect in space.

       两直线相交成直角时，称为垂直相交或正交。

       如图 4-13(a)所示，已知直线 AB 与直线 BC 在空间相互垂直，AB 平行于 H 面。因为 AB⊥BC、AB⊥Bb，由几何定理可知：AB 必垂直 BC 和 Bb 所决定的平面 Q 及 Q 面上的任一直线，如：BC1、BC2、cb……，又已知 AB∥ab，所以 ab 也必垂直于 Q 面及Q 面上的任一直线，即 ab⊥cb，其投影如图 4-13(b)所示。

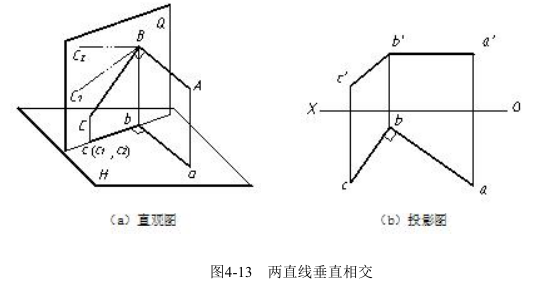
       由此可得：如果两直线垂直相交，只要其中一条直线为投影面平行线，则在所平行的投影面上两直线的同面投影垂直相交，即交角投影为直角。此特性称为直角投影定理。

      应指出的是：两直线一个投影为直角，在空间不一定垂直，只有符合直角投影定理在空间才是一对垂直的直线。

3.两直线交叉

      两直线既不平行又不相交称为交叉。

      Skew line: there are two lines which are not parallel or perpendicular to each other.

      交叉两直线的投影特性是：各面投影既不符合两直线平行的投影特性，也不符合两直线相交的投影特性，如图 4-14 所示。

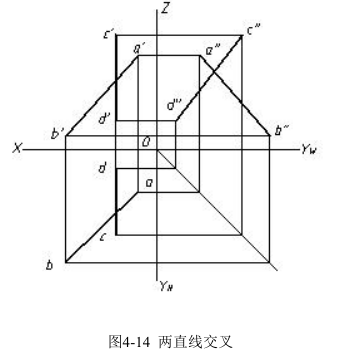
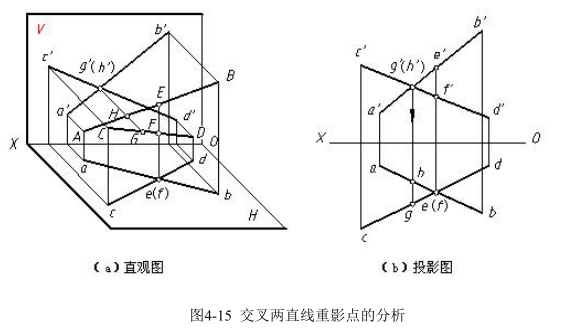
      交叉两直线的投影也可能有一组、两组甚至三组是相交的，但它们的交点不符合点的投影规律，是重影点的投影，如图 4-15（a）所示。

      判断交叉两直线重影点可见性的步骤为：从重影点入手画一根垂直于投影轴的直线到另一个投影，就可以得到重影点不重合的两个投影点，两个点中坐标值大的点为可见点，坐标值小的点为不可见点，不可见点的投影应加括号，如图 4-15(b)所示。

New words and important phrases:

Projection of point：点的投影    projection of line：直线的投影

General line：一般位置直线 : bracket:括号

Parallel line: horizontal line, frontal line and profile line

Vertical line: H -perpendicular line, V-perpendicular line, W-perpendicular line 。

Coordinate value: 坐标值

In line with, in accordance with : 符合 Decision condition: 判定条件

Skew [skju] line: 交叉直线 Intersect line: 相交直线 Parallel line: 平行直线

Subordination [səˌbɔ:dɪ'neɪʃn] 从属性