【教学目标】

1.了解方程、不等式、函数的图像之间的联系。

2.掌握一元二次不等式的图像解法。

3.通过一元二次不等式的学习，培养计算技能和观察能力。

4.通过现代信息技术应用的学习，培养计算工具使用技能。

【学习重点】

1.定义：

形如：a+bx+c>0（≥0）或a+bx+c<0（≤0）的不等式（其中a≠0），叫做一元二次不等式。

满足一元二次不等式的未知数的取值范围，叫做这个不等式的解集。

2.解法：

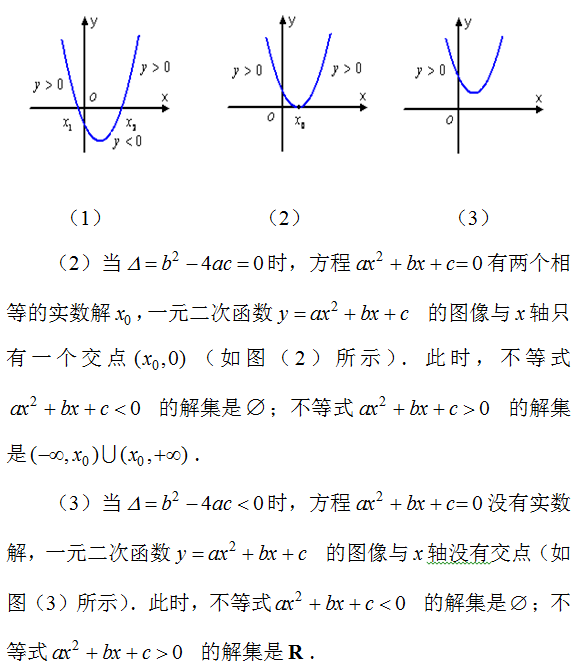
3.步骤：

（1）判断二次项系数是否为正数，如果不是，那么将不等式两边同时乘以－1；

（2）判断对应方程解的情况，如果有解，求出方程的解；

（3）根据上表写出一元二次不等式的解集。

【课后练习】