【学习目标】

1.了解 “α+k·360° ”、“ -α”、“180°±α ”的诱导公式。

2.会利用简化公式将任意角的三角函数的转化为锐角的三角函数。

3.会利用计算器求任意角的三角函数值。

4.培养学生的数学思维能力及应用计算工具的能力。

【学习重点】

1.任意角的三角函数转化为0°-360°范围内的角的三角函数：

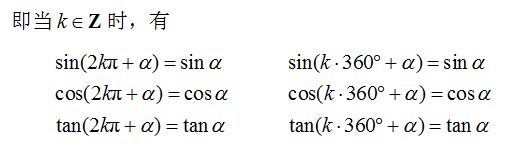
2.负角的三角函数转化为正角的三角函数：

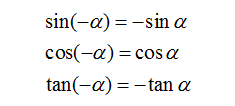
3.诱导公式：

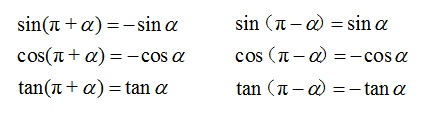
这些公式的正负号可以用口诀：“ 加全为正，负角余弦正， 减正弦正， 加正切弦正”来记忆．利用它们可以把任意角的三角函数转化为锐角的三角函数。

【课后练习】