-
1 对流换热问题的数...
-
2 练习
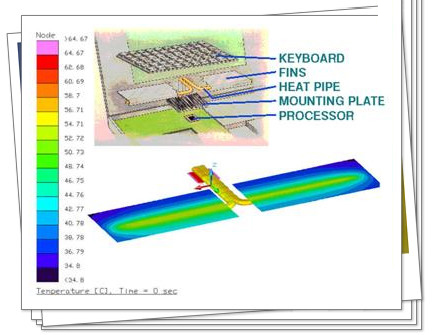
温度梯度或温度场取决于流体热物性、流动状况(层流或紊流)、流速的大小及其分布、表面粗糙度等 Þ 温度场取决于流动场
基本假设:
(1)不可压缩的牛顿型流体-空气、水以及许多工业用油类都可看作是牛顿流体,泥浆、钻井液、一定温度范围内的稠油、高凝油等均不能看作是非牛顿流体
(2)常物性
(3)忽略粘性摩擦引起的耗散作用
一 能量守恒方程
能量微分方程式描述流体温度场—能量守恒
研究对象:从流场中分离出来的微元六面体(体积dV),时间间隔为dτ
推导依据:三大守恒定律——质量守恒定律、热力学第一定律、动量定理
简化假定:
(1)二维流动;
(2)不可压牛顿流体;
(3)常物性、无内热源
(4)忽略粘性耗散热(高速流动除外)
导热引起净热量+热对流引起的净热量=微元体内能的增量
1、导热引起的净热量


X方向热对流带入微元体的焓
![]()
X方向热对流带出微元体的焓
![]()
X方向热对流引起的净热量
同理:y方向热对流引起的净热量
热对流引起的净热量
简化得
微元体内能增量
带入右上角能量守恒式

整理得二维、常物性、无内热源的能量微分方程
非稳态项 + 对流项 = 扩散项
从能量微分方程式可以看出:
方程中包含速度,说明对流换热的温度场受速度场影响。如果流体的速度为0,则退化为无内热源的导热问题。
可见,为了求得温度分布,还必须知道速度分布。
因此还要建立描述速度分布的动量微分方程式。
二 动量守恒方程(N-S方程)
动量微分方程式描述流体速度场,可以从微元体的动量守恒分析中建立

作用力:体积力、表面力
![]()

(1)— 惯性项;
(2)— 体积力;
(3)— 总压强梯度;
(4)— 粘滞力
对于稳态流动:
![]()
只有重力场时:
 三 连续性方程 (质量守恒方程)
三 连续性方程 (质量守恒方程)
流体的连续流动遵循质量守恒规律
从流场中 (x, y) 处取出边长为 dx、dy 的微元体
(z方向为单位长度),
如图所示, 质量流量为M [kg/s]
分别写出微元体各方向的质量流量分量:
![]()
![]()
X方向
![]()
单位时间内、沿x轴方向流入微元体的净质量:
![]()
同理,单位时间内、沿y轴方向流入微元体的净质量:
![]()
单位时间内微元体内流体质量的变化:
流入微元体的净质量 = 微元体内流体质量的变化
![]()
对于二维、稳态流动、密度为常数时:
对于不可压缩、常物性、无内热源的二维问题,微分方程组为:

即连续性方程
对于不可压缩、常物性、无内热源的二维问题,微分方程组为:
换热方程
连续性方程
![]()
动量方程

能量方程

解此方程组可求得速度场(u,v)和温度场(t)以及压力场(p), 既适用于层流,也适用于紊流(瞬时值)
五 定解条件:能单值地反映对流换热过程特点的条件
定解条件包括四项:几何、物理、时间、边界
(1) 几何条件 说明对流换热过程中的几何形状和大小等,平板、圆管;竖直圆管、水平圆管;长度、直径等
(2) 物理条件 说明对流换热过程的物理特征
(3) 时间条件 说明在时间上对流换热过程的特点稳态对流。换热过程不需要时间条件——与时间无关
(4) 边界条件 边界条件可分为二类:第一类、第二类边界条件
第一类边界条件:已知任一瞬间对流换热过程边界上的温度值
第二类边界条件:已知任一瞬间对流换热过程边界上的热流密度值


