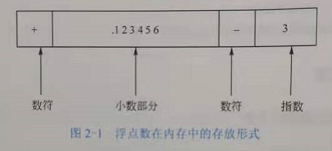
-
1 文字讲解
-
2 拓展资料
-
3 视频讲解
-
4 过关测试
一、《常量和变量》电子书籍
二、《常量》同步学习辅导
三、《整型》小结
整型数在计算机内存中的存储方式是采用补码形式进行存储。
所有编码:要理解为“有一定规律的、由相关符号组成的”一种表示方法,类似于身份证号码。
以下讲解均以短整型数为例,其它整形类似。
短整型分有符号短整型(short)和无符号短整型(unsigned short)两类,所占存储空间为 2 个字节。
1、有符号短整型(short):
(1) 范围如下图所示(-32768 至 32767):
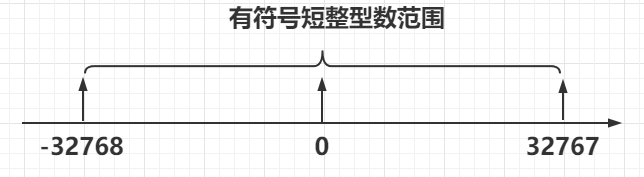
(2) 有符号短整型数二进制位构成规律:
① 0 表示正数,1 表示负数。
② 最高位为符号位,其余各位为数值位。
③ short型分配为16位二进制位。
④ 整个数值位有 15 位。
⑤ int 或 long 型分配为32位二进制位。
(3) 有符号正短整型数 与 无符号正短整数关系:
正整数的原码、反码、补码都一样,转换为无符号整数也是一样。
(4)有符号负整数的原码、反码、补码
① 负整数的原码,最高位为符号位1,其余各位与二进制各位相同。
符号位 数值位
如 -1转换为二进制真值 : - 000 0000 0000 0001
-1转换为二进制原码 : 1 000 0000 0000 0001
② 负整数的反码,符号位不变,数值位按位取反,即 1 变 0,0 变 1。
-1转换为二进制反码 : 1 111 1111 1111 1110
③ 负整数的补码,符号位不变, 负整数的反码加1。
-1转换为二进制补码: 1 111 1111 1111 1111
结论:有符号负短整数 -1 在内存中表现为: 1 111 1111 1111 1111
2、无符号短整型(short):
(1)范围如下图所示(0 至 65535):
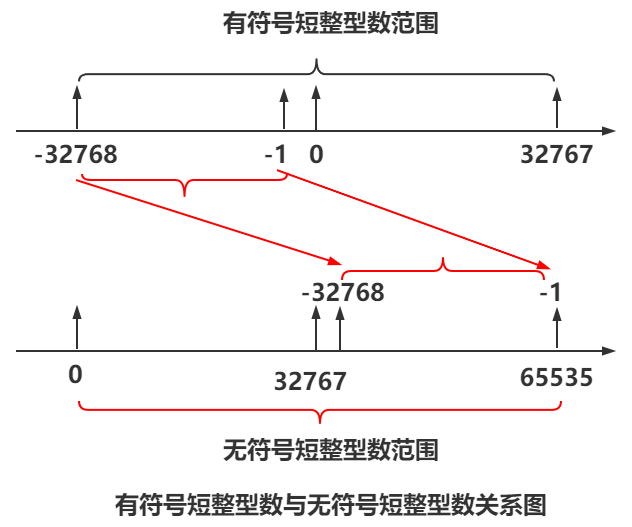
(2)无符号短整型数二进制位构成规律:
① 最高位不再表示符号位,而是数值位。
② 整个数值位有 16 位。
③ short型分配为16位二进制位。
已知 - 1 的二进制补码为: 1111 1111 1111 1111
则将 - 1 的二进制补码 1111 1111 1111 1111 转换为 十进制数:
结果为 -1 = 65535
结论:负整数转换为无符号整数,则很大。
例题:已知源程序如下:
#include <stdio.h>
main( )
{
unsigned short a = -1;
unsigned short b = -2;
unsigned short x = -32767;
unsigned short y = -32768;
printf("%u,%u\n",a,b);
printf("%u,%u\n",x,y);
}
运行结果为:
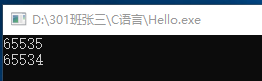
符号位 数 值 位
x的15位二进制数: - 000 0000 0000 0001
x的16位二进制原码: 1 000 0000 0000 0001
x的16位二进制反码: 1 111 1111 1111 1110
x的16位二进制补码: 1 111 1111 1111 1111
因 x 为无符号短整型数。
所以,最高位不再为符号位,而是数值位。
所以 x = 2的16方-1=65535
同理,y = -2,为无符号短整型数:
所以,最高位不再为符号位,而是数值位。
所以 y = 2的16方-2=65534
有符号短整型数的范围为 -32768 至 + 32767
结论,所有负有符号短整型数转换为无符号短整型数后,其值均大于32767。
注意:只要理解上面的结论,考试时就不会出错。