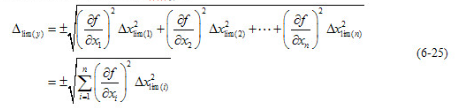-
1 内容
-
2 练习
-
3 资源下载
6.2 测量误差与测量数据的处理
6.2.1 测量误差及其表示方法
1测量误差及其表示方法
测量结果与被测对象真值在数值上的偏离或偏高程度称为量误差。测量误差可用绝对误差或相对误差来表示。
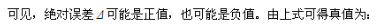
由上式，可以通过被测几何量的测量结果和绝对误差来估算其真值所在的范围。测量误差的绝对值越小，量结果就越接近于真值，则测量精度也就越高；反之，测量精度就越低。绝对误差可在评定或比较大小相同的被测几何量中反映测量精度。
2）相对误差ε
相对误差是绝对误差的绝对值与真值之比。由于真值很难得到，因此在实际应用中常用测量结果近似代替真值进行估算，即：
对于大小不相同的被测几何量，则需要用相对误差来评定或比较它们的测量精度。
2测量误差的来源
测误差的来源通常可归纳为以下几方面。
（1）计量器具的误差
计童器具的误差是指计量器具本身所固有的误差，包括计童器具的设计、制造和使用过程的各项误差，这些误差综合表现在示值误差和重复精度上。设计计量器具时，为了简化结构而采用近似设计，或者设计的计童器具不符合阿贝原则等，都会产生测量误差。
阿贝原则是指测量长度时，应将基准线安放在被测长度的延长线上，或顺次排成一条直线。如图3所示，用千分尺测量轴径，千分尺的标准线与工件被测直径在同一直线上，即符合阿贝原则。如果测微螺杆轴线与被测直径间存在一夹角φ，由此产生的测量误差δ为：
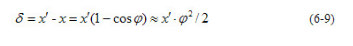
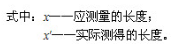
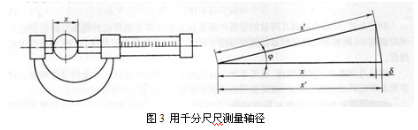
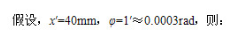
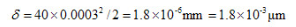
可见，符合阿见原烈的计量器具本身引起的测量误差很小，可以忽略不计。
（2）测量原理误差
测量原理误差是指测至时，由于选用的测量原理不完善而引起的误差，包括计算公式、测量操作、工件安装、定位等精度不高引起的误差。
（3）环境误差
环境误差是指实际测量时的环境条件与标准的测量环境条件有偏差而引起的测量误差。测量条件包括温度、湿度、气压、振动、灰尘等，其中温度的影响最为显著。
图样上标注的各种尺寸、公差和极限偏差都是以标准温度20℃为依据的。在测量时，如果实际温度偏离标准温度，而被测零件和计重器具材料的线胀系数又不同，那么，由于物体热胀冷缩，温度变化将引起测量误差。此时的测量误差可由下式计算：
（4）人员误差
人员误差是指测量时由于测量人员自身因素所引起的测量误差，包括测量人员的技术熟练程度、分辨能力、连续工作的疲劳程度等。例如，测量人员使用计童器具不熟练、量值估读不同等都会产生测量误差。
值得注意的是，测量误差与测量错误是不同的概念。
3测量误差的分类
测至误差按其性质可分为系统误差、随机误差和粗大误差三大类。
（1）系统误差
系统误差是指在一定的测量条件下，对同一被测几何量进行连续多次测量时，误差的大小和符号保持不变或按一定规律变化的测量误差。前者称为定值系统误差，后者称为变值系统误差。
（2）随机误差
随机误差是指在一定测量条件下，连续多次测量同一被测几何量时，误差的大小和符号以不可预定的方式变化的测量误差。随机误差主要是由测量过程中一些无法预料的偶然因素或不稳定因素引起的。
（3）粗大误差
粗大误差是指超出规定条件下预计的测量误差，也称过失误差。粗大误差是由某些不正常原因造成的。
4测量精度
测量精度是指被测几何量的测得值与其真值相接近的程度，与测量精度相对的概念是测量误差。测量误差越大，测量精度越低；反之，测量精度就越高。为了反映不同性质的测量误差对测量结果的不同影响，测量精度可分为以下几类：
①正确度。在一定测量条件下，对被测几何量进行连续多次测量，各测得值的平均值与真值相一致的程度。它表示测量结果受系统误差影响的程度。
②精密度。在一定测量条件下进行连续多次测量，各测得值之间相互接近的程度。它表示测量结果受随机误差影响的程度。
③准确度（也称精确度）.在一定测量条件下进行连续多次测量，测得值与其真值相接近的程度。它表示测量结果受系统误差和随机误差综合影响的程度。
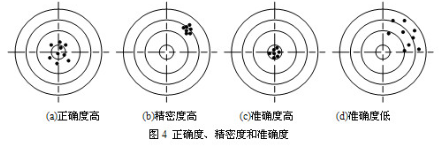
现以射击打靶为例说明上述概念。如图4所示，图中小圆圈表示靶心，黑点表示弹孔。圈4a表示随机误差大而系统误差小，即打靶的正确度高而精密度低；图4b表示随机误差小而系统误差大，即打靶的精密度高而正确度低；图4r表示系统误差和随机误差均小，即打靶的准确度高；图4d表示系统误差和随机误差均大，即打靶的准确度低.
由此可知，在实际测量中，正确度高，精密度却不一定高；精密度高，正确度却不一定高；但准确度高，则正确度和精密度就一定高。
6.2.2 测量数据的处理
1测量列中随机误差的处理
1）随机误差的特点及分布规律
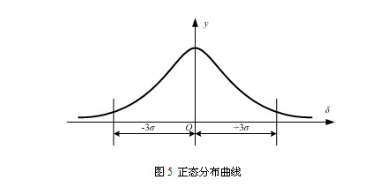
大量实验表明，测量时的随机误差通常服丛正态分布规律，其正态分布曲线如图5所示。正态分布的随机误差具有下列4个基本特性：
①单峰性。绝对值越小的随机误差出现的概率越大，反之则越小。
②对称性。绝对值相等的正、负随机误差出现的概率相等。
③有界性。在一定测量条件下，随机误差的绝对值不会超过一定的界限。
④抵偿性。随着测量次数的增加，随机误差的算术平均值超近于零。
2）随机误差的评定指标
评定随机误差分布特性时，以正态分布曲线的标准偏差作为评定指标，根据概率论，正态分布曲线的数学表达式为：
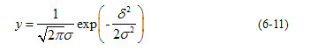
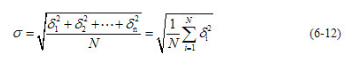
标准偏差σ是反映测量列中数据分散程度的一项指标，它是测量列中任一测量值的标准偏差。由于随机误差具有有界性，其大小不会超过一定的范围，因此随机误差的极限值就是测量极限误差。
3）随机误差的置信截率与极限值
由概率论可知，随机误差正态分布曲线与横坐标轴所包围的面积等于所有随机误差出现的概率总和。如果随机误差落在区间（-，+
）中，则其概率为：
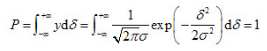
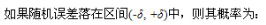
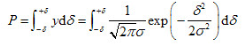
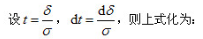
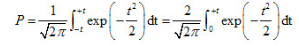
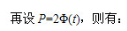
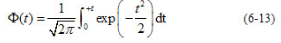
由此可见，随机误差超出士3σ范围的概率仅为0.27%，这样，绝对值大于30的随机误差出现的可能性几乎等于零。因此，可以将随机误差的极限值，即侧量极限误差取为士3σ，并记作：
（3）计算测量列中单次测得值的标准偏差与单次测量结果的表达
测得值的算术平均值虽然表示测量结果，但不能表示各测得值的精密度，故需要确定标准偏差，对有限次数的测量，通常按下面的贝塞尔（Bessel）公式计算单次测得值的标准偏差：
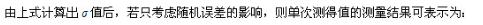
这意味着用单次测值作为测量结果与被测量真值（或算术平均值）之差不超出其极限误差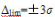
的范围，此时置信概率为99.73%。
（4）计算测量列算术平均值的标准偏差与测量列测量结果的表达
若一定条件下，对同一被测几何童进行多姐测量（每组测量N次），则对应每组测量都有一个算术平均值，因而得到一列算术平均值。这些算术平均值各不相同，分布在真值附近，其分布范围比单次测得值的分布范围小得多，也就是说，算术平均值的精密度比单次测得值的精密度要高。多组测量的算术平均值的分布特性，同样可用标准偏差作为评定指标.
根据误差理论，测量列算术平均值的标准偏差与该测量列单次测得值的标准偏差存在如下关系：
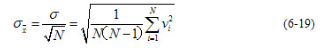
由上式可知，测量次数N越多，则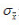
越小，测量的精密度就越高，但测量次数也不宜过多，一般取N=10-15次为宜。
测量列算术平均值的测量极限误差为：
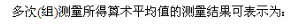
这意味着用测量列各视得值的算术平均值作为测量结果与被测堂真值之差不会超出其极限误差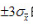
的范围，此时置信概率为99.73%。
2测量列中系统误差的处理
对系统误差，应寻找和分析其产生的原因及变化规律，以便从测量数据中发现并予以消除，从而提高测量精度。
（1）定值系统误差的处理
定值系统误差的大小和符号均保持不变，因此它不改变测量误差分布曲线的形状，而只改变测量误差分布中心的位置。从测量列的原始数据本身看不出定值系统误差是否存在，要揭露定值系统误差，可以采用实验对比法，即变测至条件通常采用高精度量），对已测量的同一被测几何进行另一组次数相同的测量，比较前后两列视得值，若两者没有差异，则表示不存在定值系统误差；若两者有差异，则表示存在定值系统误差。
（2）变值系统误差的处理
变值系统误差的大小和符号按一定规律变化，因此它不仅改变测量误差分布曲线的形状，而且改变测量误差分布中心的位置。可用残差观察法来发现变值系统误差，即将各测得值的残差按测顺序排列，观察其分布规律。若各残差大体上正、负相间，又无显著变化，则不存在变值系统误差；若备残差按近似的线性规律递增或递减，则可判定存在线性系统误差；若各残差的大小和符号有规律地周期变化，则存在周期性系统误差。
消除变值系统误差的方法很多。例如，周期性系统误差可采用半周期法来消除，即取各处每州隔半个周期的两个测量数据的平均值作为一个测得值。
根据已掌握的程度，系统误差也可分为已定系统误差和未定系统误差：前者是指数值大小和变化规律已被掌握的系统误差；而后者是指数值大小和变化规律未被掌握的系统误差。对于已定系统误差，可按上述方法加以处理：而对于未定系统误差，则可以按处理随机误差的方法进行处理。
从理论上讲，系统误差有一定规律，是可以消除的。但实际上，由于系统误差存在的复杂性，因此只能减小到一定程度。一般说来，系统误差若能减小到使其影响相当于随机误差的程度，则可认为已被消除。
3测量列中粗大误差的处理
粗大误差的数值相当大，在测量中应尽可能避免。如果粗大误差已产生，则应根据判断大误差的准则子以易服余，通常用拉依达（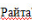
）准则来判断。
拉依达准则又称3σ准则。该准则认为：当测量列服从正态分布时，残差落在士3σ外的概率仅为0.27%，因此，当测量列中出现绝对值大于3σ的残差时，即：
5间接测量列的数据处理
间接测量时，被测几何量是与之有一定关系的各个实测几何量的函救。因此，间接测量中，被测几何量的测量误差也是各个实测几何量的测量误差的函数，它属于函数误差。
（1）函数误差的基本计算公式
设间接测量中被测几何量y与各实测几何量
之间的函数关系为：
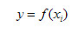
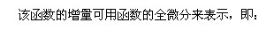
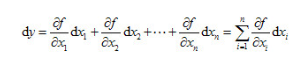
（2）函敬已定系统误差的计算
若各实测几何量x的测得值中存在已定系统误差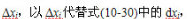
则可按下式求的函数函散已定系统误差
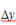以为：
