3.6 几何误差

3.6.1 实际要素的体现

      测量几何误差时，难天测遍整个实际要素来取得无限多测点的数据，而是考虑现有计量器具及测量本身的可行性和经济性，采用均匀布置测点的方法，测量一定数量的离散测点来代替整个实际要素。此外，为了测量方便与可能，尤其是测量方向、位置误差时，实际导出要素（中心要素）常用模拟的方法体现。例如用V形块体现实际轴颈的轴线。用模拟法体现实际尺寸要素（轮廓要素）对应的导出要素时，排除了实际导出要素的形状误差。

3.6.2 几何误差及其评定

       几何误差是指实际被测要素对其理想要素的变动量，是几何公差的控制对象。几何误差值不大于相应的几何公差值，则认为合格。

     1.形状误差及其评定

      形状误差是指实际单一要素对其理想要素的变动量，理想要素的位置应符合最小条件。最小条件就是理想要素处于符合最小条件的位置时，实际单一要素对理想要素的最大变动量为最小。对于实际单一组成要素（如实际表面、轮廓线），这理想要素位于该实际要素的实体之外且与它接触。对于实际单一导出要素（如实际轴线），这理想要素位于该实际要素的中心位置。

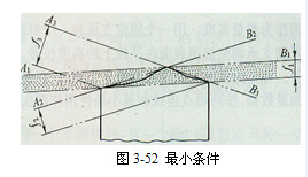
      参看图3-52的示例，评定给定平面内的轮廓线的直线度误差时，有许多条位于不同位置的理想直线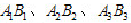，用它们评定的直线度的误差值分别为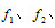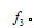这些理想直线中必有一条（也只有一条）理想直线即直线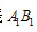能使实际被测轮廓线对它的最大变动量为最小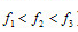（），因此理想直线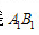的位置符合最小条件，实际被测轮廓线的直线度误差值为。

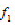       评定形状误差时，按最小条件的要求，用最小包容区域（简称最小区域）的宽度或直径来表示形状误差值。所谓最小包容区域，是指包容实际单一要素时具有最小宽度或直径的包容区域。各个形状误差项目的最小包容区域的形状分别与各自的公差带形状相同，但前者的宽度或直径则由实际单一要素本身决定。

         直线度误差值应该采用最小包容区域来评定，其判别准则如图3-53所示：由两条平行直线包容实际被测直线s时，S上至少有高、低、高相间（或者低、高、低相间）三个极点分别与这两条平行直线接触，则这两条平行直线之间的区域U即为最小包容区域，该区域的宽度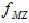即为符合定义的直线度误差值。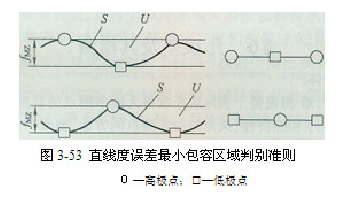

   （2）平面度误差值的评定

     平面度误差值应该采用最小包容区域来评定，其判别准则如图3-54所示：由两个平行平面包容实际被测表面S时，S上至少有四个极点分别与这两个平行平面接触，且满足下列两个条件之一，那么这两个平行平面之间的区域U即为最小包容区域，该区域的宽度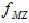，即为符合定义的平面度误差值。

     ①三角形准则：至少有三个高（低）极点与一个平面接触，有一个低（高）极点与另一个平面接触，并且这一个低高）极点的投影落在上述三个高（低）极点连成的三角形内，或者落在该三角形的一条边上。

     ②交叉准则：至少有两个高极点和两个低极点分别与这两个平行平面接触，并且两个高极点的连线和两个低极点的连线在空间呈交叉状态，或者有两个高（低）极点与两个平行包容平面中的一个平面接触，还有一个低高）极点与另一个平面接触，且该低（高）极点的投影落在两个高（低）极点的连线上。

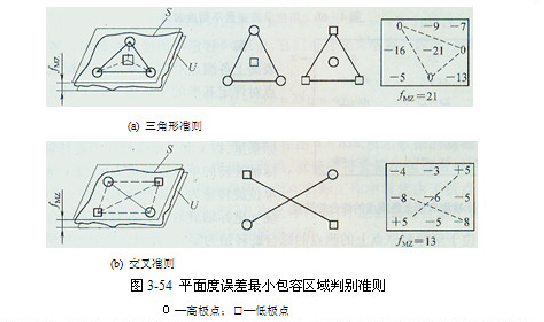
      平面度误差值还可以用对角线平面来评定。这种评定方法是指以通过实际被测表面的一条对角线（两个角点的连线）且平行另一条对角线（其余两个角点的连线）的平面作为评定基准，取各测点相对于它的偏离值中最大偏离值（正值或零）与最小偏离值（零或负值）之差作为平面度误差值。

    （3）圆度误差值的评定

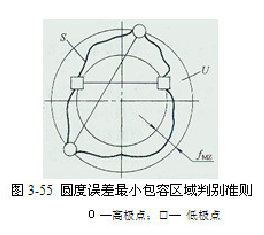
      圆度误差值应该采用最小包容区域来评定，其判别准则如图3-55所示：由两个同心圆包容实际被测圆S时，S上至少有4个极点内、外相间地与这两个同心圆接触至少有两个内极点与内圆接触，两个外极点与外圆接触），则这两个同心圆之间的区域U即为最小包容区域，该区域的宽度即这两个同心圆的半径差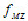就是符合定义的圆度误差值。

      圆度误差值也可以用由实际被测圆确定的最小二柔圆作为评定基准来评定圆度误差值，取最小二乘圆圆心至实际被测圆的轮廓的最大距离与最小距离之差作为圆度误差值。

      圆度误差值还可以用由实际被测圆确定的最小外接圆（仅用于轴）或最大内接圆（仅用于孔）作为评定基准来评定圆度误差值。

     2.方向误差及其评定

     方向误差是指实际关联要素对其具有确定方向的理想要素的变动量，理想要素的方向由基准确定。

     参看图3-56，评定方向误差时，在理想要素相对于基准A的方向保持图样上给定的几何关系（平行、垂直或倾斜某一理论正确角度）的前提下，应使实际被测要素S对理想要素的最大变动量为最小。对于实际关联组成要素，这理想要素位于该实际要素的实体之外且与它接触。对于实际关联导出要素，这理想要素位于该实际要素的中心位置。

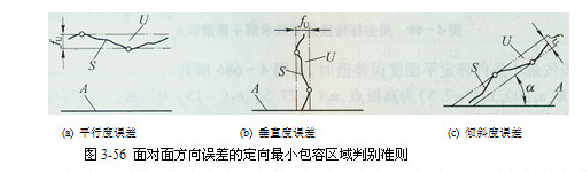
       方向误差值用对基准保持所要求方向的定向最小包容区域U（简称定向最小区域）的宽度来表示。定向最小包容区域的形状与方向公差带的形状相同，但前者的宽度或直径则由实际关联要素本身决定。如图3-56所示，由具有确定方向的两平行平面包容实际关联要素S时，S上至少有两个极点（高、低极点或左、右极点）分别与这两平行平面接触，则两平行平面间区域U即为定向最小包容区域，其宽度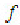即为符合定义的方向误差值。

     3.位置误差及其评定

      位置误差是指实际关联要素对其具有确定位置的理想要素的变动量，理想要素的位置由基淮和理论正确尺寸确定。

      位置误差值用定位最小包容区域（简称定位最小区域）的宽度或直径来表示。定位最小包容区域是指以理想要素的位置为中心来对称地包容实际关联要素时具有最小宽度或最小直径的包容区域。定位最小包容区域的形状与位置公差带的形状相同，但前者的宽度或直径则由实际关联要素本身决定。通常，实际关联要素上只有一个测点与定位最小包容区域接触。位置误差值等于这个接触点至理想要素所在位置的距离的两倍。

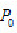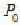      例如图3-57a所示，评定图3-29所示零件的位置度误差时，理想平面所在的位置（评定基准）由基准平面A和理论正确尺寸确定。定位最小包容区域U为对称配置于的两平行平面之间的区域，实际被测要素S上只有一个测点与U接触，位置度误差值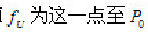的距离的两倍。图3-57b中，评定图3-23所示零件上孔的轴线位置度误差时，设该孔的实际轴线用心轴轴线模拟体现，这实际轴线用一个点S表示；理想轴线的位置（评定基准）由基准A、B和理论正确尺寸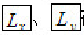确定，用点O表示。以点O为圆心，以OS为半径作圆，则该圆内的区域就是定位最小包容区域U。位置度误差值新。 

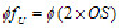本节课件

相关网址： 
[1] 标准化管理委员会http://www.sac.gov.cn/
[2]国家质监总局http://www.aqsiq.gov.cn/
[3] 机械工程学报 http://www.cjmenet.com.cn/
[4] 计量学报 http:// www.jlxb.china-csm.org
[5] 中国机械工程 http://www.cmemo.org.cn/
[6] 机床与液压 http://www.jcyyy.com.cn/
[7] 制造技术与机床 http://www.mtmt.com.cn/
[8] 组合机床与自动化加工技术 http://www.zhjcz.com.cn/
[9] 机械设计与研究 http://www.jofmdr.com/
[10] 计算机集成制造系统 http://cims.diamt.net.cn/
[11] 机械设计 http://jxsj.qikann.com/
[12] 仪器仪表学报 http://www.yqybxb.qikann.com/

本节课件

相关网址： 
[1] 标准化管理委员会http://www.sac.gov.cn/
[2]国家质监总局http://www.aqsiq.gov.cn/
[3] 机械工程学报 http://www.cjmenet.com.cn/
[4] 计量学报 http:// www.jlxb.china-csm.org
[5] 中国机械工程 http://www.cmemo.org.cn/
[6] 机床与液压 http://www.jcyyy.com.cn/
[7] 制造技术与机床 http://www.mtmt.com.cn/
[8] 组合机床与自动化加工技术 http://www.zhjcz.com.cn/
[9] 机械设计与研究 http://www.jofmdr.com/
[10] 计算机集成制造系统 http://cims.diamt.net.cn/
[11] 机械设计 http://jxsj.qikann.com/
[12] 仪器仪表学报 http://www.yqybxb.qikann.com/