授课题目：第八章   空间解析几何与向量代数 

                     §1 向量及其线性运算

授课方式： 回忆+互动

教学目的与要求：

1.理解掌握向量的基本概念、向量的线性运算；

2.理解掌握空间直角坐标系、向量的线性运算的坐标表示、向量的模、方向角、投影；

3.理解掌握空间两点的距离公式并能熟练灵活应用.

4.理解掌握向量的模、方向角、投影等基本概念并会熟练计算。

主 要 内 容 ( 按 教 学 大 纲 要 求 )：

§1  向量及其线性运算                         

一、向量概念

1.向量及其表示

2.自由向量、单位向量、零向量

3.向量的相等、平行、共线、共面

二、向量的线性运算

1．向量的加减法

三角形法则、平行四边形法则、向量加法的运算规律

向量加法的多边形法则、负向量、向量的差

2．向量与数的乘法

数乘向量的定义、数乘向量的运算规律、例1

定理1（两向量平行的充要条件）、说明（P293）

三、空间直角坐标系  

坐标轴、坐标面、卦限、向量的坐标分解式、向量及点的坐标、向径、坐标面上和坐标轴上点的坐标特征      

 四、利用坐标作向量的线性运算 

向量加法的坐标表示式、数乘向量的坐标表示式

两向量平行的充要条件

例2、例3                    

五、向量的模、方向角、投影

1．向量的模与两点间的距离公式

例4、例5、例6

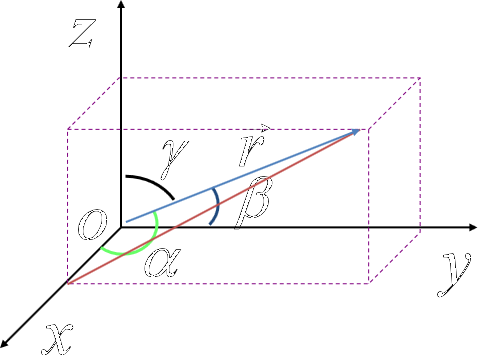
2．方向角与方向余弦

例7、例8

3．向量在轴上的投影

向量在轴上的投影及其性质1、2、3

例9                       

                            

重点难点：

1.重点：向量的基本概念；向量的线性运算；空间直角坐标系；向量的模、方向角、投影；向量平行的充要条件；

2.难点：向量的线性运算及运算规律；向量的模、方向角、向量在轴上的投影

外语词汇： Vector; unit vector; zero vector; parallel; linear operation of vector; triangle rule; parallelogram rule; commutative law; associative law; negative vector; difference; distributive law; space rectangular coordinates; coordinate plane; octant; modulus of vector; angle between vector a and b; direction angle; projection of a vector onto an axis

复习思考题、课堂测试题、课外作业 ：

习题 8--1：     1；2；3；4；5；6；7；8；9；10