2.4.1  画平行线

1.两块三角板配合使用，一块固定，一块移动，可画出任意倾斜方向的平行线，如图2-18所示。

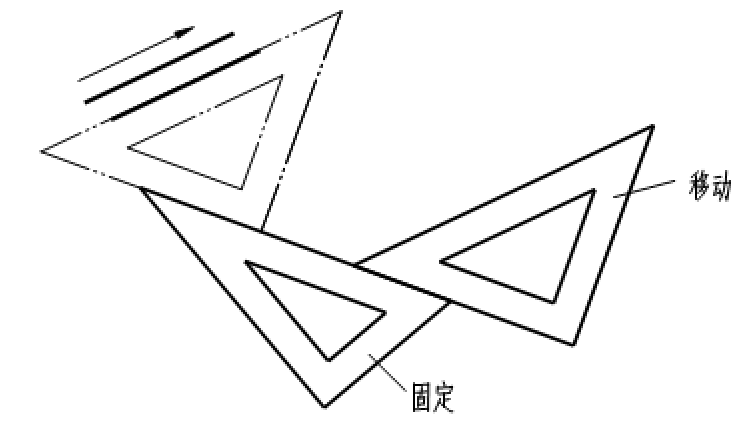
图2-18  画平行线   

2.4.2  等分线段 

等分线段可以用平行线法。已知线段AB，需要将其进行5等分。

 (1)过线段AB的一个端点A作一条任意方向的直线AC,用分规以任意距离在线段AC上量得1、2、3、4、5个等分点，如图2-19(a)所示。

 (2)连接线段AC上的等分点5和线段AB的端点B,然后通过线段AC上的其他等分点作线段5B的平行线，与AB的交点即为线段AB的各等分点，如图2-19(b)所示。

     

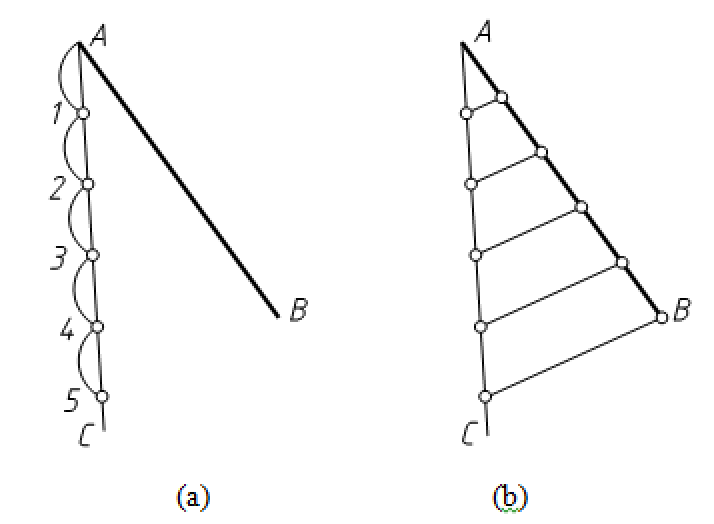
    图2-19 等分线段的画法

2.4.3  作正多边形 

 1.正六边形

  (1)已知正六边形的外接圆，以圆的象限点A、B为圆心，用圆规等分圆周作正六边形，如图2-20(a)所示。

  (2)已知正六边形的外接圆或内切圆，利用30º/60º三角板和丁字尺配合使用作正六边形，如图2-20(b)所示。

图2-20  正六边形的画法

 2.正n边形

已知正n边形的外接圆，以n=7为例说明正n边形的画法。

 (1)作正n边形外接圆直径AB的7等分点，如图2-21(a)所示。

(2)以点A为圆心，AB为半径画弧交外接圆水平直径延长线于M、N两点。连接1N、2N、5N (也可连接直径上的偶数点)，如图2-21(b)所示。

 (3)延长1N、2N、5N分别于外接圆相交，同理连接1M、2M、5M并延长于外接圆相交，连接交点和B点得到正七边形，如图2-21(c)所示。

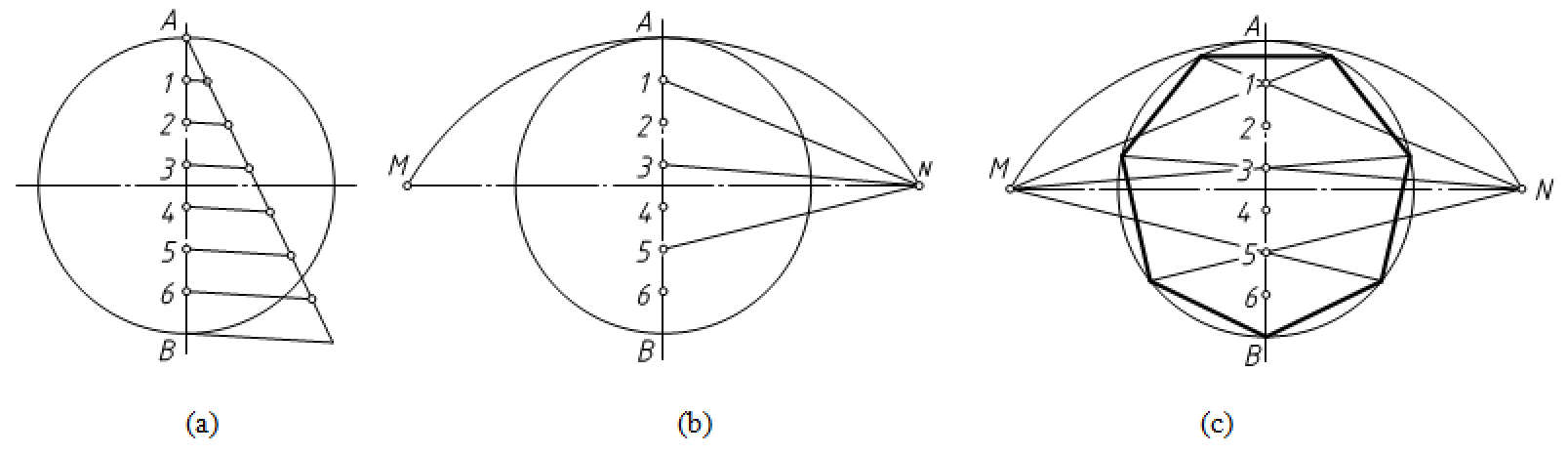
                         图2-21  正n边形的画法 

2.4.4  圆弧连接 

1. 圆弧连接的原理

圆弧连接，是指用一段已知半径的圆弧将两已知线段(圆弧)光滑连接的作图方法。这里讲的连接，指圆弧与线段或圆弧与圆弧的连接处是相切的，因此，在作图的时候，应准确地求出连接圆弧的圆心和切点的位置。

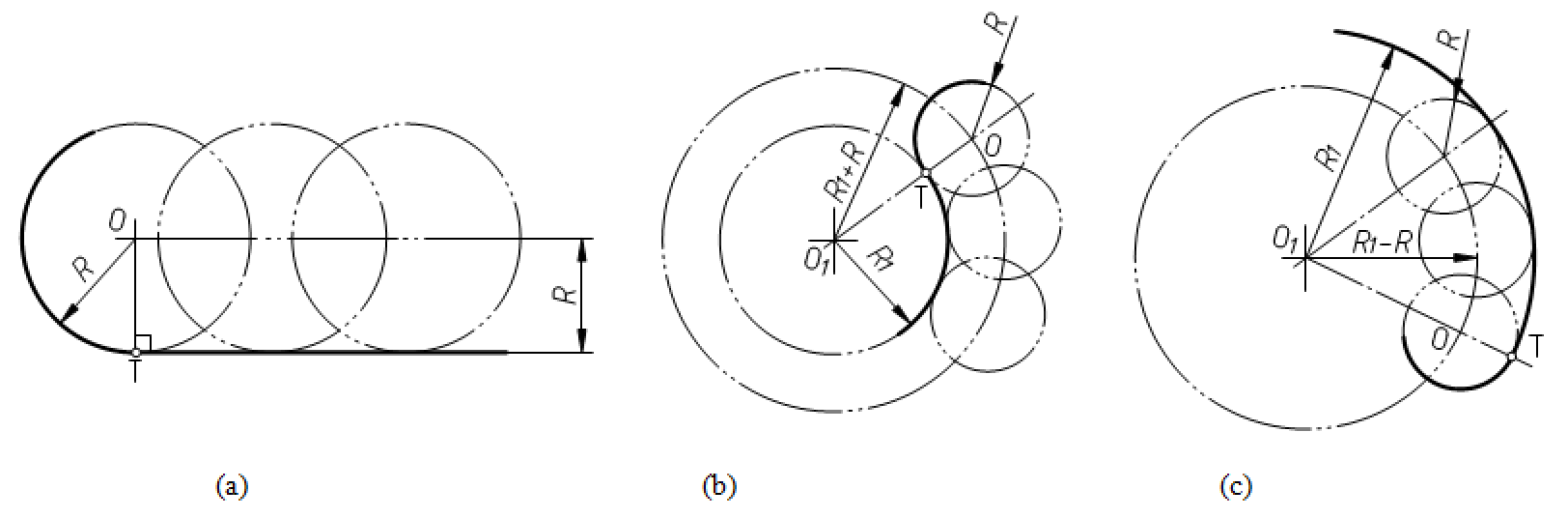
图2-22  圆弧的连接

 (1)半径为R的圆弧与已知直线相切，其圆心轨迹是距离直线为R的平行线。若连接圆弧的圆心为O时，由O向直线作垂线，垂足T即为切点，如图2-22(a)所示。

 (2)半径为R的圆弧与已知圆弧(圆心为O₁，半径为R₁)相切，其圆心轨迹是已知圆弧的同心圆。当两圆弧外切时，半径等于R₁+R，如图2-22(b)所示；当两圆弧内切时，半径等于R₁-R，如图2-22(c)所示。若连接圆弧的圆心为O时，连接两圆心的直线O₁O与已知圆弧的交点T，即为切点。

2. 圆弧连接的作图方法

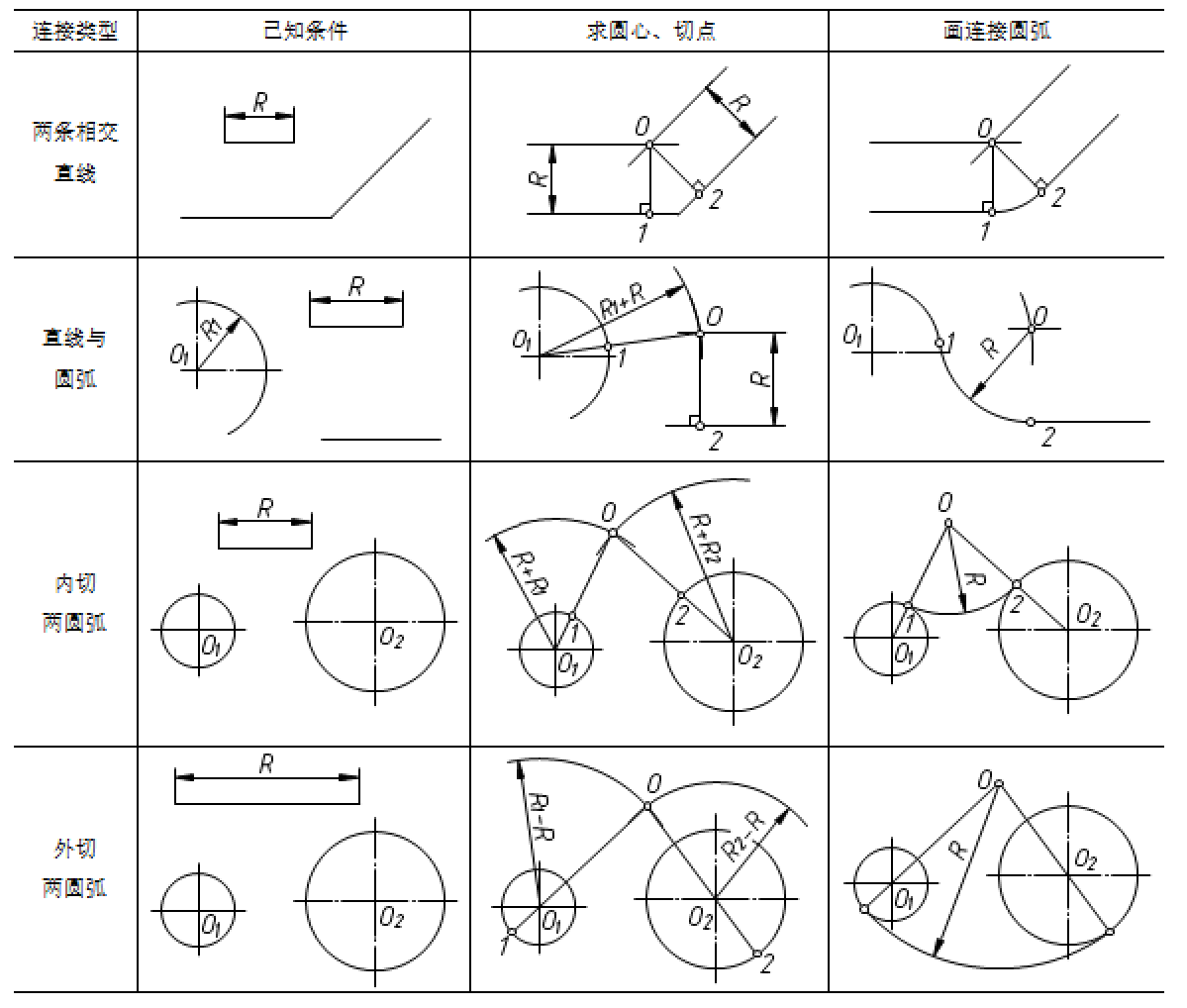
表2-5给出的是已知连接圆弧半径为R的四种连接形式的作图方法。

表2-5圆弧连接示例