3.2.1 投影法

在日常生活中，当阳光和灯光照射物体时，会在地面上和墙壁上出现该物体的影子。人们根据这个现象，加以科学的抽象，提出利用投影来表达物体，即为投影法。

空间有一个平面P以及不在该平面上的点A及点光源S，自点光源S经过A点向平面P作线，与平面交于a点。a称为空间点A在平面P上的投影，S称为投射中心，P称为投影面，直线SAa称为投影线。投影法是投影线通过物体，向选定的平面投射，并在该面得到投影的方法。

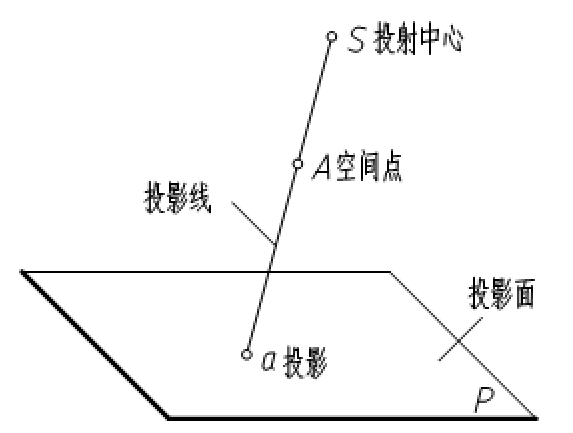
图3-1  投影法

3.2.2 投影法的分类

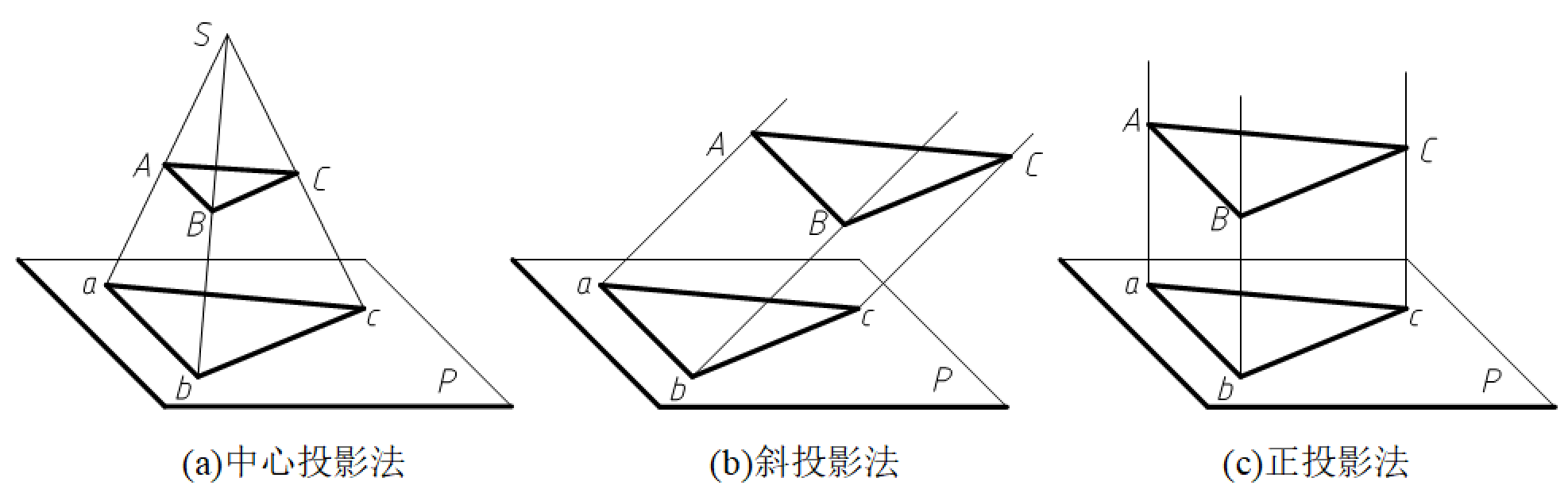
图3-2  投影法的分类

1.中心投影法

投影线汇交于一点的投影法称为中心投影法，如图3-2(a)所示。中心投影法得到投影的大小随着物体与投影面之间距离的变化而改变，一般不反映物体的实际大小，中心投影法多用于绘制建筑上的透视图，如图3-3所示。

图3-3  透视图

2. 平行投影法

投影线互相平行的投影法称为平行投影法。投影线与投影面倾斜的平行投影法，称为斜投影法，如图3-2(b)所示。投影线与投影面垂直的平行投影法，称为正投影法，如图3-2(c)所示。

与中心投影法不同，平行投影法得到的投影大小同物体与投影面的距离没有关系，投影的度量性比较好。轴测投影图中利用斜投影法绘制轴测图，如图3-4所示。正投影能够真实地表达空间物体的形状和大小，因此在工程技术上使用的工程图样多采用正投影绘制，如图3-5所示，通常将“正投影”简称为“投影”。

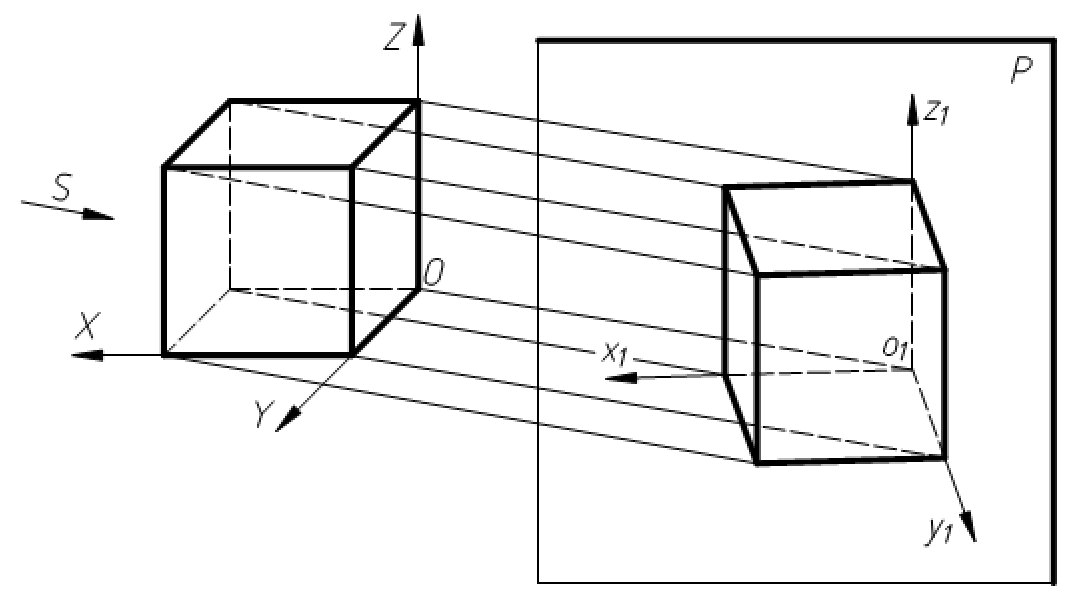
图3-4 轴测投影 

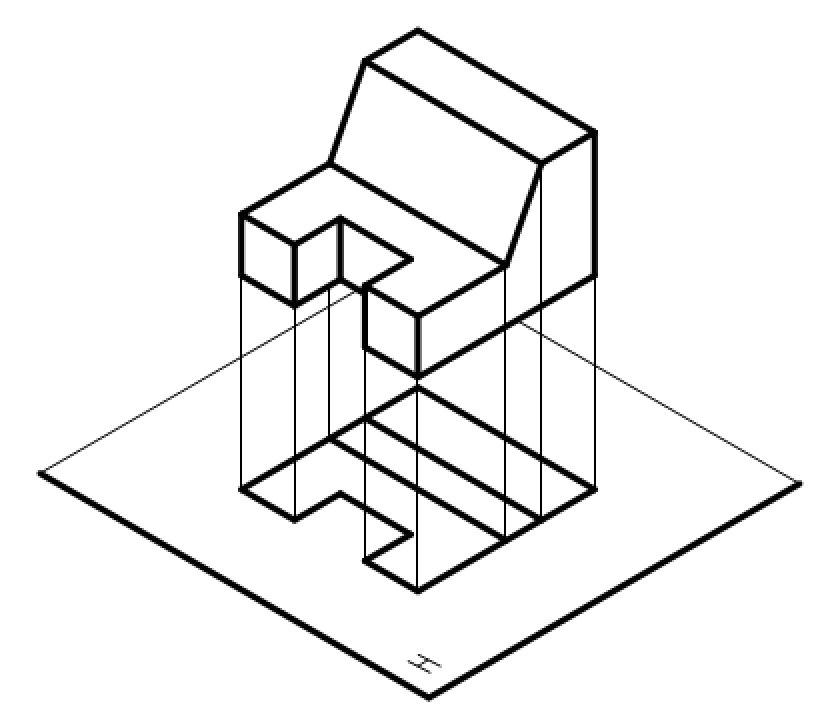
  图3-5 正投影视图

3.2.3 正投影法的基本性质

1. 积聚性

直线垂直于投影面，其投影积聚成点；平面图形垂直于投影面，其投影积聚成一条直线，如图3-6(a)所示。

2. 显实性

直线平行于投影面，其投影反映直线的实长；平面图形平行于投影面，其投影反映平面图形的实形，如图3-6(b)所示。

3. 类似性

直线倾斜于投影面，其投影的长度短于直线实际的长度；平面图形倾斜于投影面，其投影为平面图形的类似形，各边在投影中的顺序保持不变，如图3-6(c)所示。

 4. 平行性、定比性

空间互相平行的直线，其投影一定平行。直线上的点分线段所成比，投影后保持不变，如图3-6(d)所示。

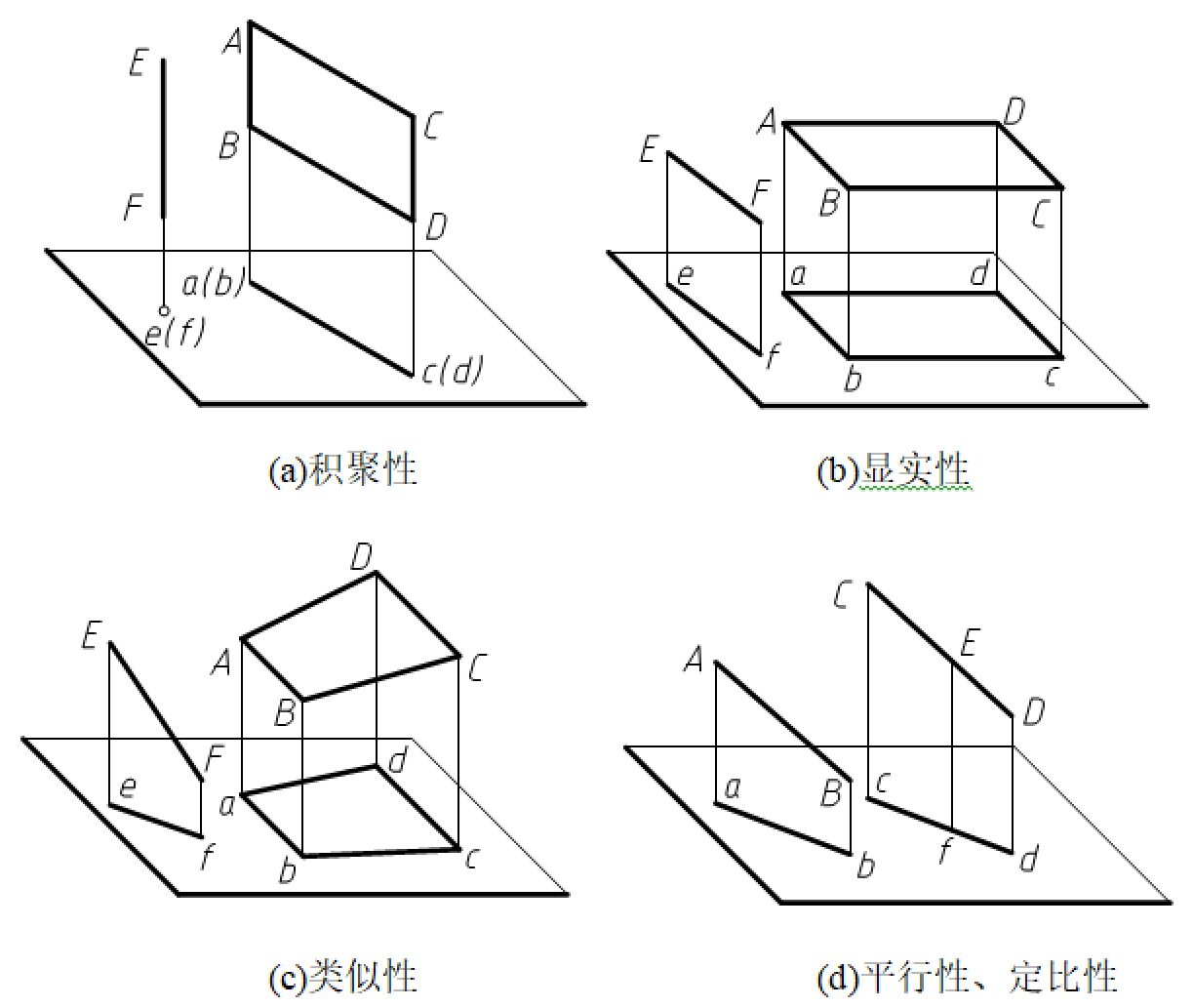
图3-6  正投影的基本性质