3.4.1  立体上点的投影

1. 点的投影

立体上点A的投影如图3-10所示。空间上的点用大写字母表示A，投影用小写字母表示：其中水平投影表示为a，正面投影表示为a'，侧面投影表示为a″。

点的三面投影的位置也必然符合“长对正，高平齐，宽相等”的投影规律。直线上的点的投影必在直线的同名投影上；平面上的点必在平面的同名投影上，若点位于平面内的一条直线上，则点必在平面上。

图3-10  立体上点的投影

2. 立体上两点的相对位置

立体上两点的相对位置是指这两个点在空间的左右、前后、上下三个方向的位置关系。主视图反映上下、左右的关系，如图3-11中的B点在A点的左、下方。主视图反映左右、前后的关系，分析图中B点在A点的后方。任意两面投影均能反映两点的相对位置。

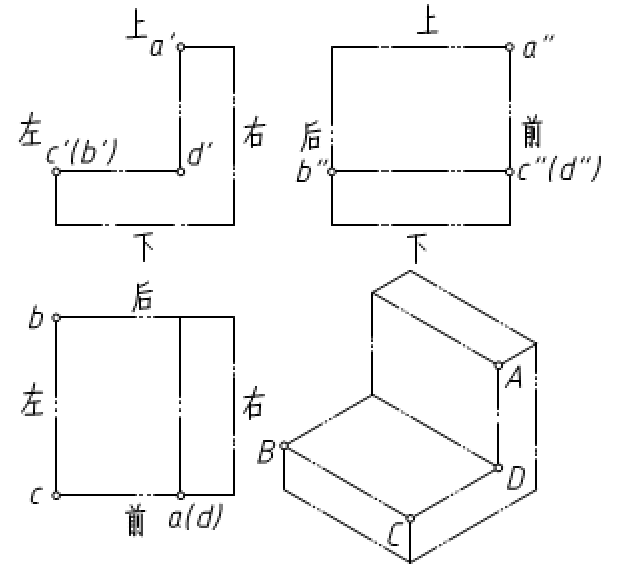
图3-11  立体上两点相对位置及重影点

3. 重影点

图3-11中A、D两点的水平投影重合为一点，则此点成为A、D两点的上下重影点 。B、C是正面的前后重影点，C、D是侧面的左右重影点。对于重影点可见性的判断原则是：前遮后，上遮下，左遮右。被遮挡的点的投影需要用括号括起来，如图中a(d)表示A点在上，D点在下，D点被遮挡。

3.4.2  立体上直线的投影

直线的投影由直线两个端点的同名投影来确定。根据直线在三面投影体系中的位置，直线分为三类，即投影面的平行线、投影面的垂直线和一般位置直线。前两类线统称为特殊位置直线。

直线与投影面的夹角，称为该直线对投影面的倾角，与水平面、正面、侧面的倾角分别用α、β、γ表示。

1. 投影面垂直线

垂直于一个投影面的直线称为投影面的垂直线。垂直正立投影面的直线称为正垂线，垂直于水平投影面的直线称为铅垂线，垂直于侧立投影面的直线称为侧垂线。投影面垂直线的投影特性如表3-1所示。

表3-1  投影面垂直线

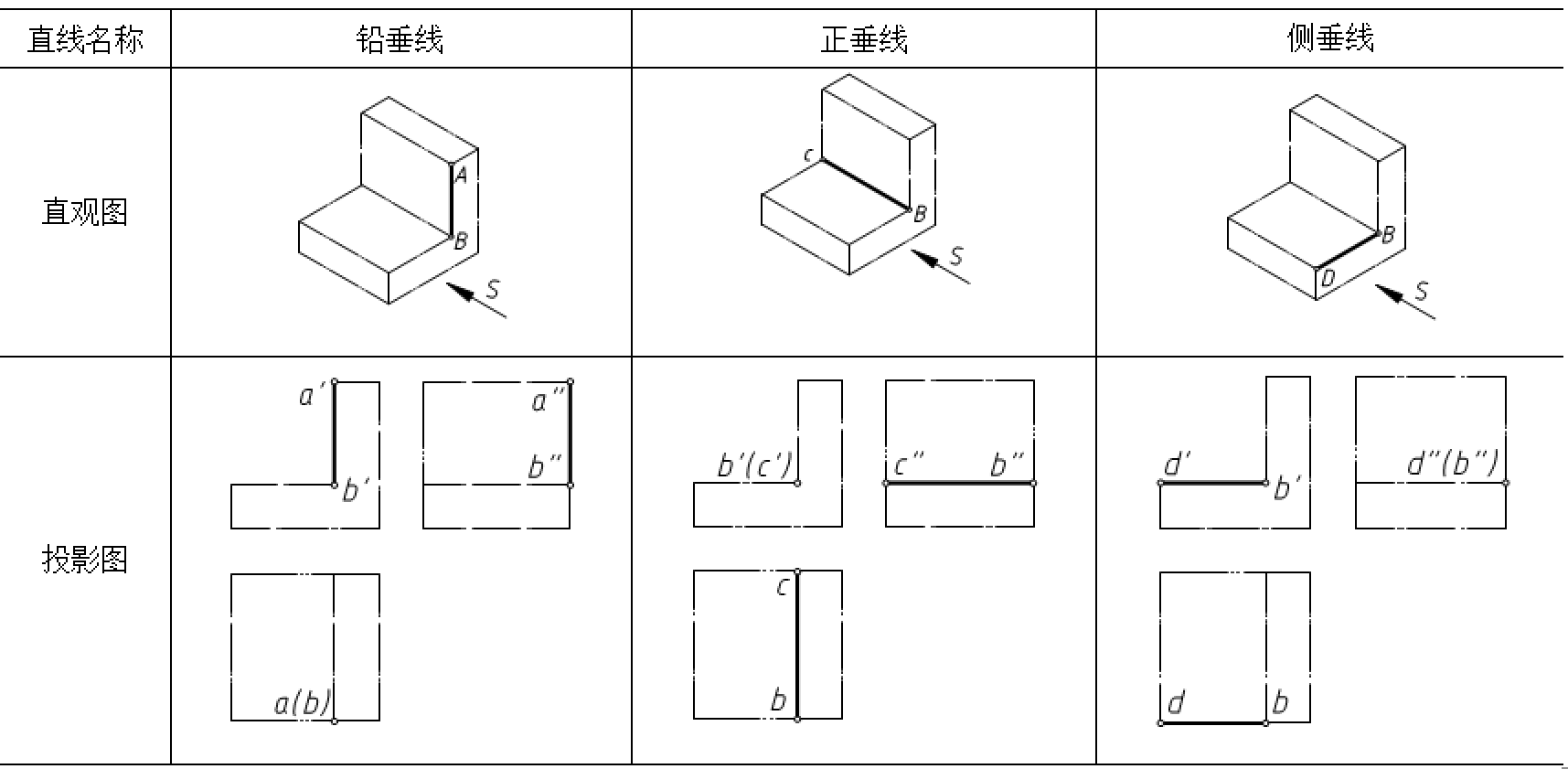
从表3-1可以得出投影面垂直线的投影特性：

(1)在直线所垂直的投影面上，直线的投影积聚成一点。

(2)在另外两个投影面上，直线的投影分别垂直于相应的投影轴，且反映直线的实长。

2. 投影面平行线

平行于一个投影面而与另外两个投影面倾斜的直线称为投影面平行线。平行于正立投影面的直线称为正平线，平行于水平投影面的直线称为水平线，平行于侧立投影面的直线称为侧平线。投影面平行线的投影特性如表3-2所示。

表3-2  投影面平行线

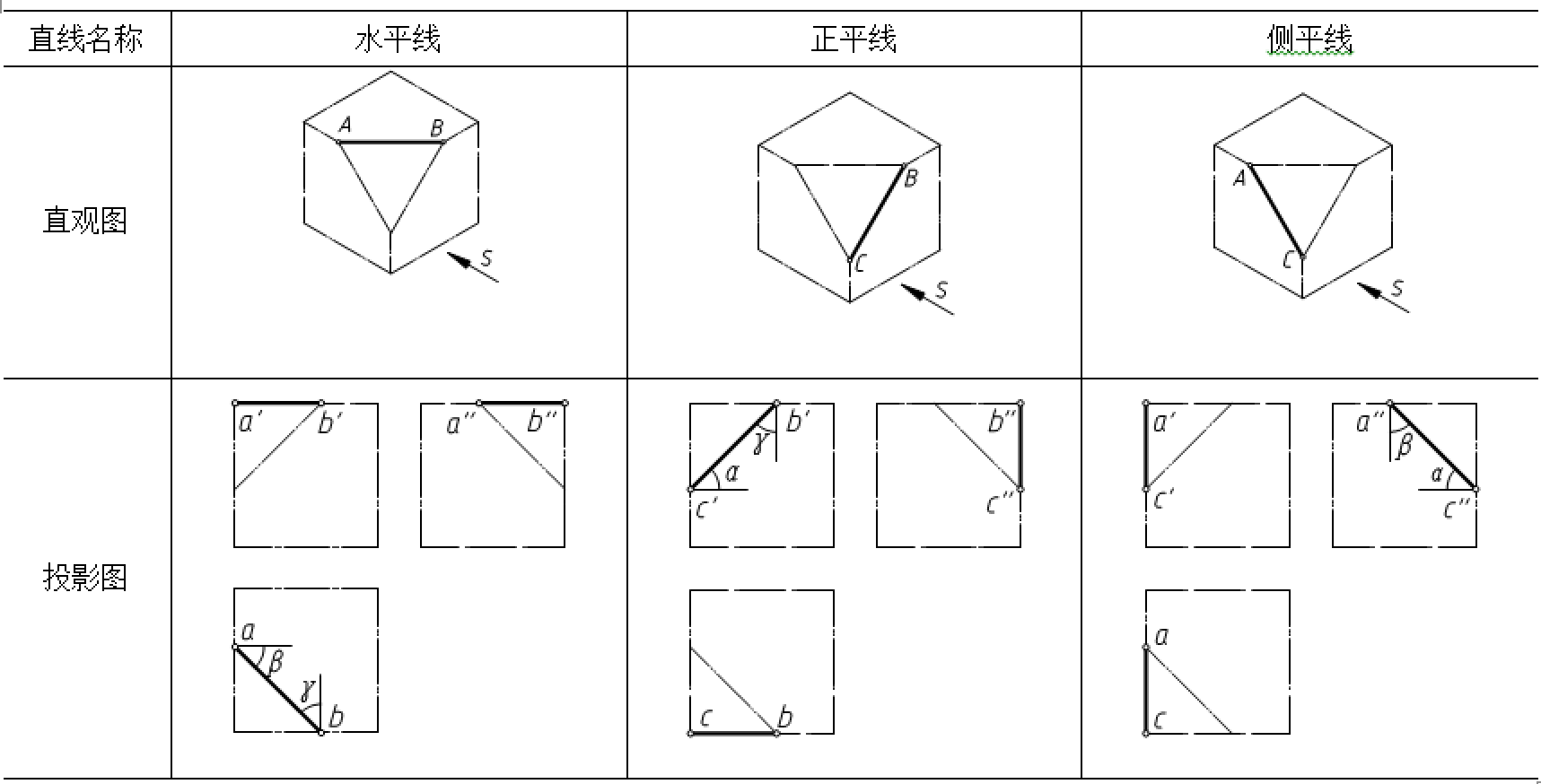
 从表3-2可以得出投影面平行线的投影特性：

 (1)在直线所平行的投影面上的投影反映实长，投影与投影轴的夹角反映直线对另外两个投影面的倾角大小。

 (2)在另外两个投影面上的投影，分别平行于相应的投影轴，且投影长度均比实长短。

 3. 一般位置直线

 与三个投影面都倾斜的直线称为一般位置直线。在图3-12中，直线SA与三个投影面都处于倾斜的位置，即为一般位置直线。

 一般位置直线的投影特性：

 (1)三个投影面的投影都与投影轴倾斜，投影的长度都比直线的实长短。

 (2)三个投影与投影轴的夹角都不反映直线与投影面倾角的真实大小。

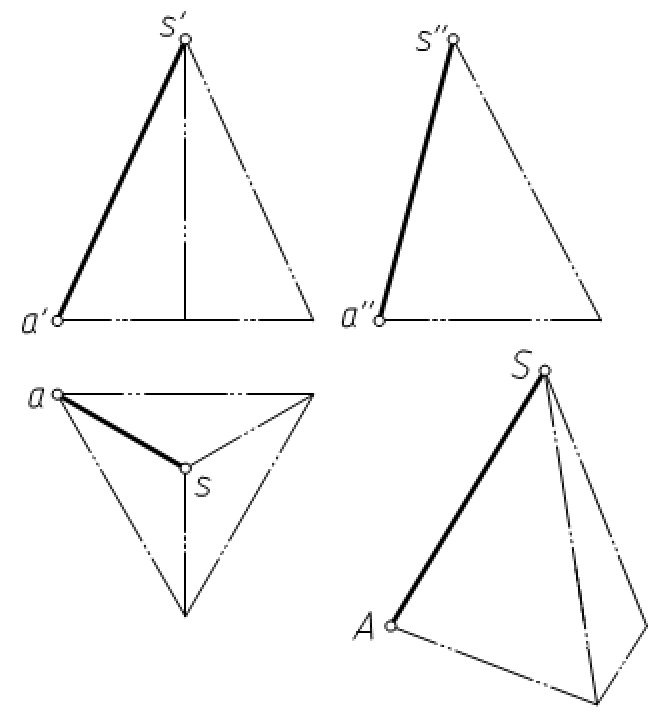
图3-12  一般位置直线

3.4.3  立体上平面的投影

根据平面在三面投影体系中的位置，平面分别三类，即投影面的垂直面、投影面的平行面和一般位置平面，前两类平面统称为特殊位置平面。

平面与投影面的夹角，称为该平面对投影面的倾角，与水平面、正面、侧面的倾角分别用α、β、γ表示。

1. 投影面垂直面

垂直于一个投影面与另两个投影面都倾斜的平面称为投影面的垂直面，垂直于正立投影面的平面称为正垂面，垂直于水平投影面的平面称为铅垂面，垂直于侧立投影面的平面称为侧垂面。投影面垂直面的投影特性如表3-3所示。

表3-3  投影面垂直面

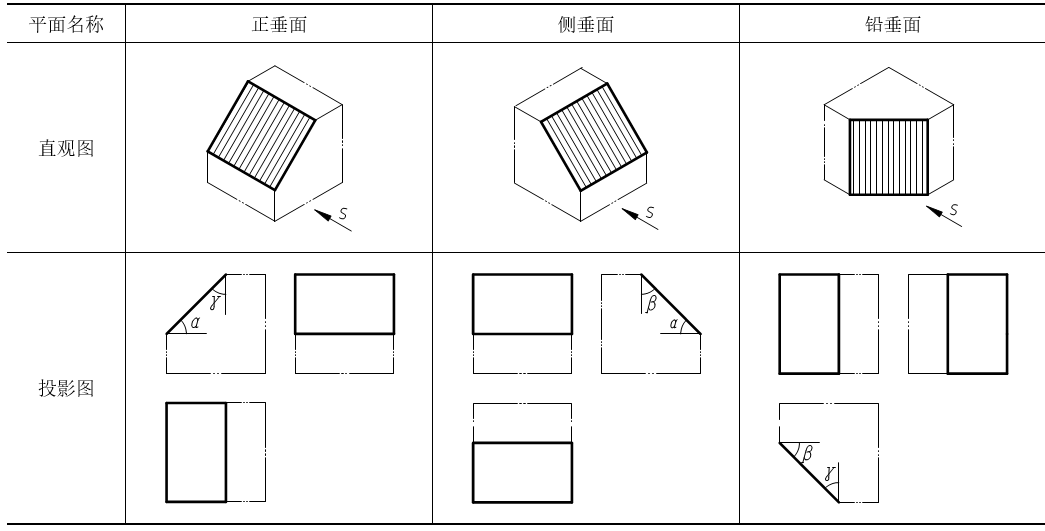
从表3-3可以得出投影面垂直面的投影特性：

(1)在所垂直的投影面上，平面投影积聚成一条直线，积聚的投影与投影轴的夹角，分别反映平面和另两个投影面的倾角。

(2)平面在另外两个投影面的投影是平面的类似形。

2.投影面平行面

平行于一个投影面即同时垂直于其它两个投影面的平面称为投影面平行面。平行于正立投影面的平面称为正平面，平行于水平投影面的平面称为水平面，平行于侧立投影面的平面称为侧平面。投影面平行面的投影特性如表3-4所示。

表3-4  投影面平行面

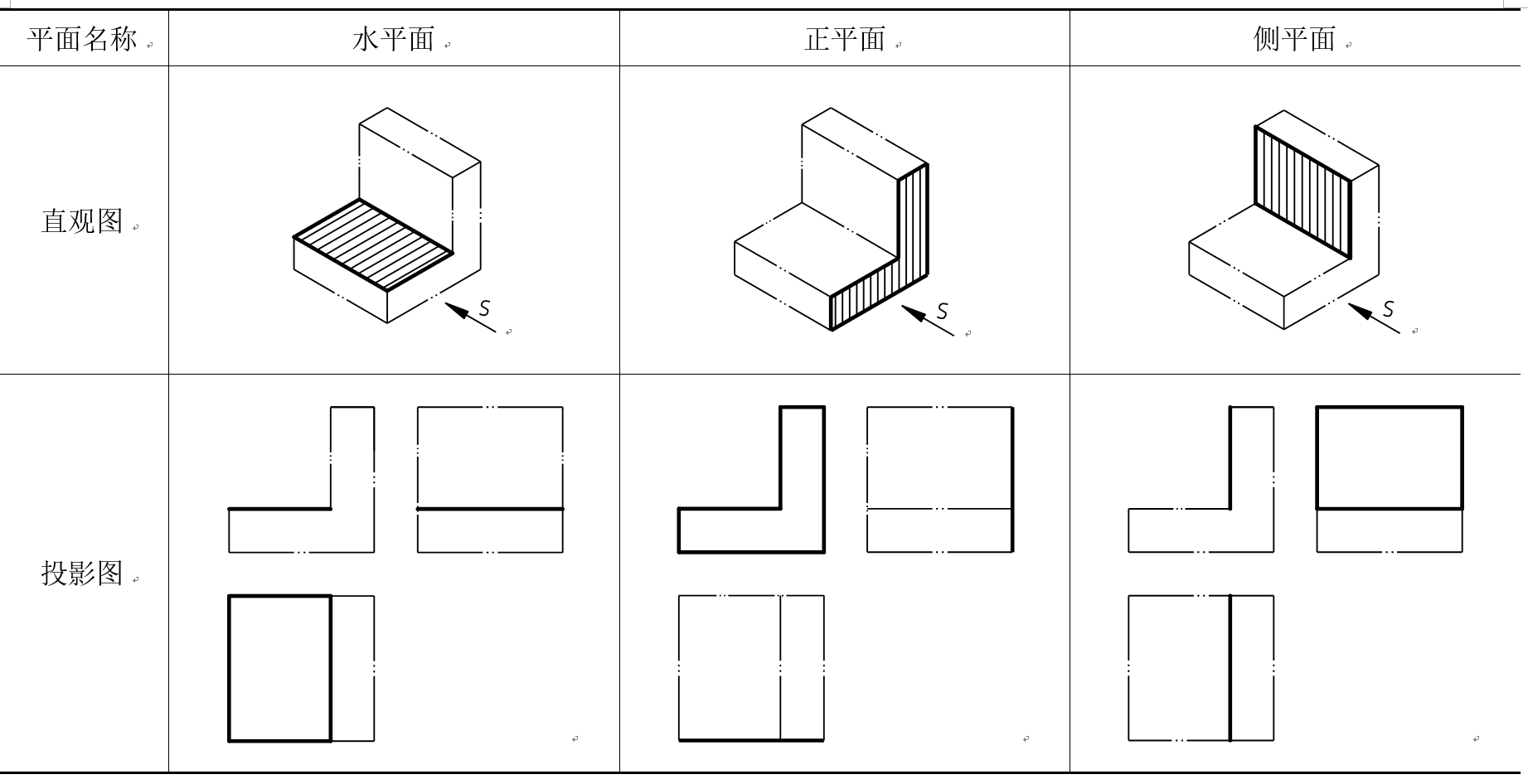
从表3-4可以得出投影面平行面的投影特性：

(1)在所平行的投影面上，平面的投影反映原形。

(2)在另外两个投影面上，平面的投影积聚成直线，且分别平行于对应的投影轴。

3. 一般位置平面

与三个投影面都处于倾斜位置的平面称为一般位置平面。图3-13中平面SAB与三个投影面都倾斜，即为一般位置平面。

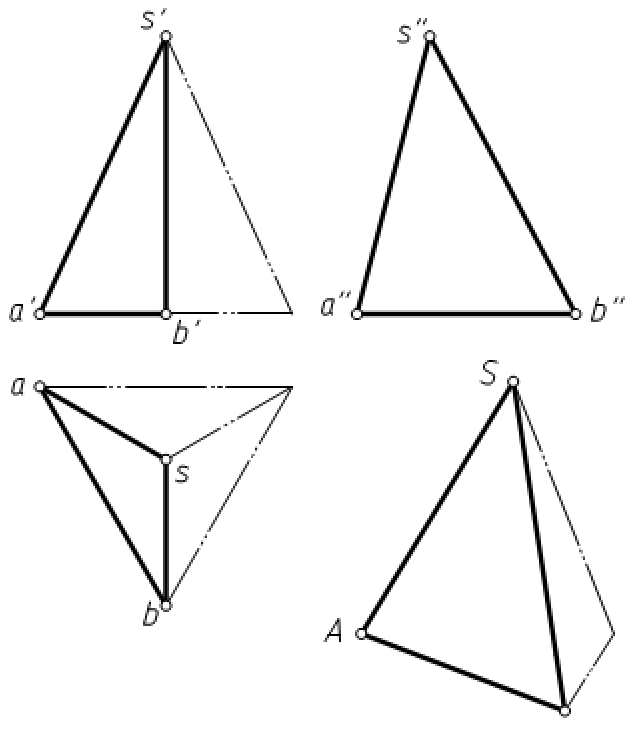
 图3-13  一般位置平面

一般位置平面的投影特性：

(1)三个投影面的投影是平面的类似形。

(2)三个投影都不反映平面与投影面倾角的真实大小。

2.3.4  一般位置平面上的点和直线的投影

(1)若点在平面内的一条直线上，则该点在该平面内。

(2)若一条直线通过平面内的两个点，则该直线必在平面内。

(3)若一条直线通过平面内一点且平行于平面内的直线，则该直线必在平面内。

例2-1  如图3-14(a)所示，在一般位置平面SAB上有一点M，已知M点的正面投影，求作M点的水平投影。

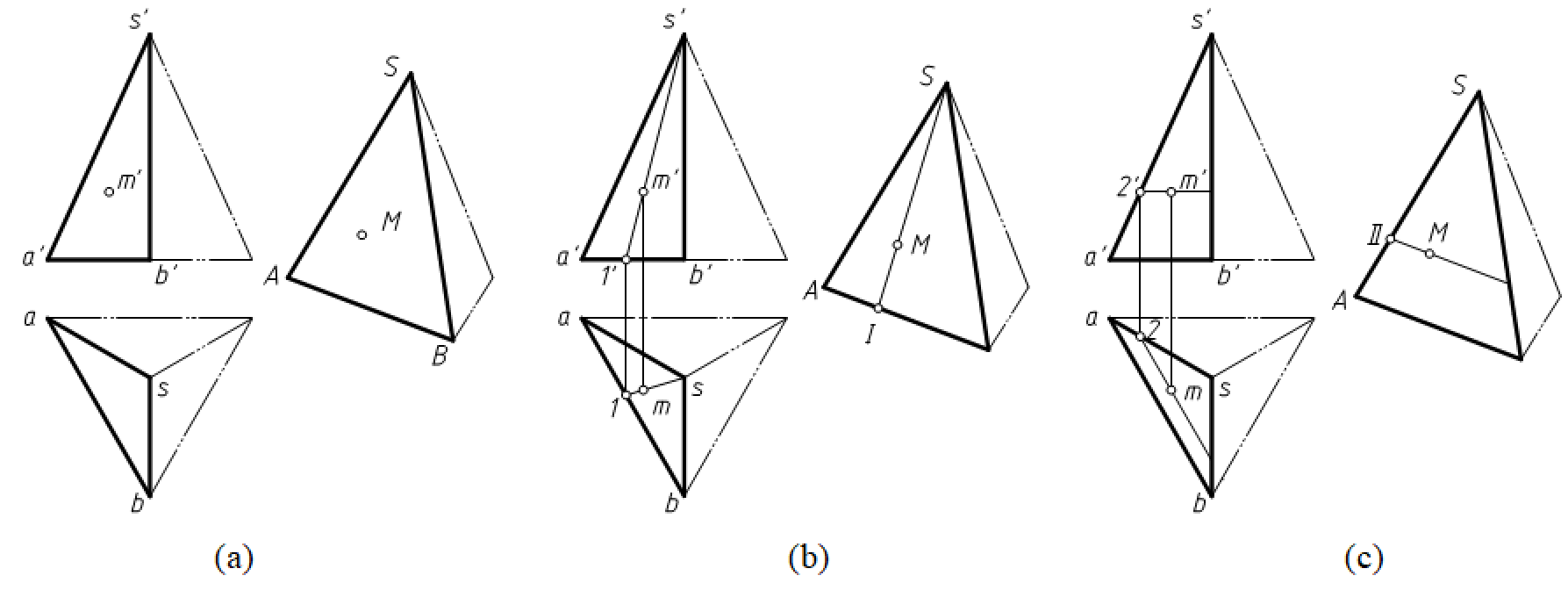
 图3-14  一般位置平面上取线

方法一：

分析  S、M两点在平面SAB上，过两点作一条直线，该直线一定在平面SAB上。M点在直线SM上，M的投影一定在直线SM的同名投影上。

作图  连接s'm'并延长交a'b'于1'，作出点Ⅰ的水平投影1，连接s1，M点水平投影在s1上，如图2-14(b)所示。

方法二：

分析 点S在平面SAB上，过点S作一条与平面SAB内的直线平行的直线，该直线一定在平面SAB上，M的投影一定在所作直线的同名投影上。

作图  过m'作直线与a'b'平行交s'a'于2'，作出点Ⅱ的水平投影2，过点2作直线ab的平行线，点M的水平投影在所作的平行线上，如图2-14(c)所示。