微积分

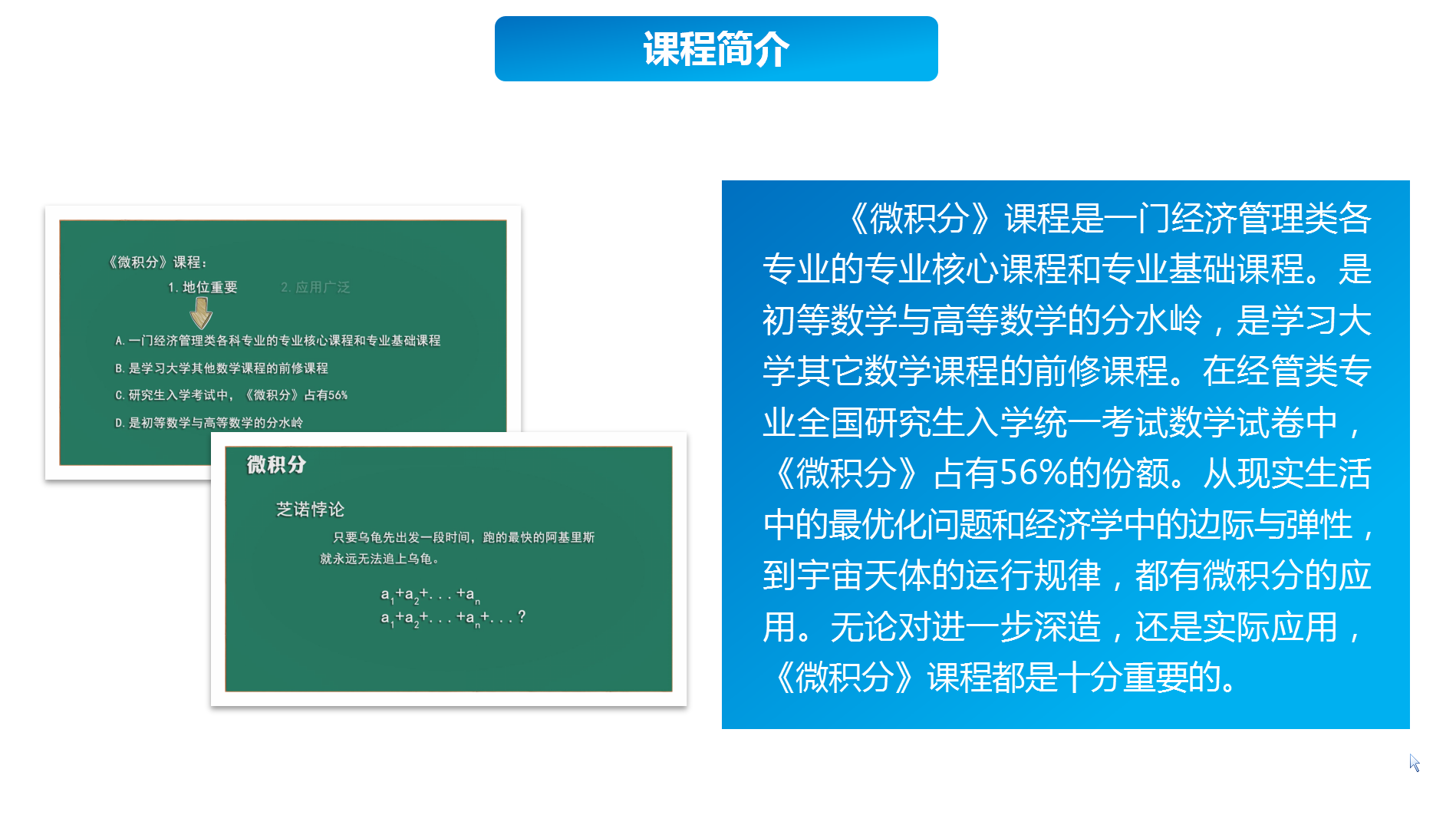
微积分研究的东西可以很大，也可以很小，还研究事物是如何变化的。微积分虽然很抽象，但它可以用来解释真实世界。微积分是生物、物理、社会科学的重要工具。走出教室，我们能看到微积分出现在我们日常生活各个角落。
这门课是易学的微积分入门课程，适合没有学过微积分的同学，或者学过了但还想复习概念和利用微积分解决实际问题的同学。通过用微积分来学习微积分，课程鼓励你参加进来。

微积分（Calculus）是高等数学中研究函数的微分（Differentiation）、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科。内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

从17世纪开始，随着社会的进步和生产力的发展，以及如航海、天文、矿山建设等许多课题要解决，数学也开始研究变化着的量，数学进入了“变量数学”时代。整个17世纪有数十位科学家为微积分的创立做了开创性的研究，但使微积分成为数学的一个重要分支的还是牛顿和莱布尼茨。

（1）运动中速度与距离的互求问题

已知物体移动的距离s 表为以时间为变量的函数s=(st)，求物体在任意时刻的速度和加速度；反过来，已知物体的加速度表为以时间为变量的函数公式，求速度和距离。这类问题是研究运动时直接出现的，困难在于，所研究的速度和加速度是每时每刻都在变化的。比如，计算物体在某时刻的瞬时速度，就不能像计算平均速度那样，用移动的距离去除运动的时间，因为在给定的瞬间，物体移动的距离和所用的时间是0。但是，根据物理，每个运动的物体在它运动的每一时刻必有速度，这也是无疑的。已知速度公式求移动距离的问题，也遇到同样的困难。因为速度每时每刻都在变化，所以不能用运动的时间乘任意时刻的速度，来得到物体移动的距离。

（2）求曲线的切线问题

这个问题本身是纯几何的，而且对于科学应用有巨大的重要性。由于研究天文的需要，光学是十七世纪的一门较重要的科学研究，透镜的设计者要研究光线通过透镜的通道，必须知道光线入射透镜的角度以便应用反射定律，这里重要的是光线与曲线的法线间的夹角，而法线是垂直于切线的，所以总是就在于求出法线或切线；另一个涉及到曲线的切线的科学问题出现于运动的研究中，求运动物体在它的轨迹上任一点上的运动方向，即轨迹的切线方向。

（3）求长度、面积、体积、与重心问题等

这些问题包括，求曲线的长度（如行星在已知时期移动的距离），曲线围成的面积，曲面围成的体积，物体的重心，一个相当大的物体（如行星）作用于另一物体上的引力。实际上，关于计算椭圆的长度的问题，就难住数学家们，以致有一段时期数学家们对这个问题的进一步工作失败了，直到下一世纪才得到新的结果。又如求面积问题，早古希腊时期人们就用穷竭法求出了一些面积和体积.他们就采用了穷竭法。当分割的份数越来越多时，所求得的结果就越来越接近所求的面积的精确值。但是，应用穷竭法，必须添上许多技艺，并且缺乏一般性，常常得不到数字解。当阿基米德的工作在欧洲闻名时，求长度、面积、体积和重心的兴趣复活了。穷竭法先是逐渐地被修改，后来由于微积分的创立而根本地修改了。

（4）求最大值和最小值问题（二次函数，属于微积分的一类）

例如炮弹在炮筒里射出，它运行的水平距离，即射程，依赖于炮筒对地面的倾斜角，即发射角。一个“实际”的问题是：求能够射出最大射程的发射角。十七世纪初期，Galileo断定（在真空中）发射角是 45度时达到最大射程；他还得出炮弹从各个不同角度发射后所达到的不同的最大高度。研究行星的运动也涉及到最大值和最小值的问题。

微积分