直线与平面、平面与平面的相对位置The position of a line relative to a plane, plane relative to a plane
一、平行问题
1.直线与平面平行
由初等几何可知,若一直线与某平面上任一直线平行,则此直线与该平面平行。反之,若一直线与某平面平行,则此平面上必能作出与该直线平行的直线。
直线AB平行于△CDE平面上一直线CF(ab∥cf,a¢b¢∥c¢f¢),故AB与平面CDE平行。
直线mn平行ab,而mn不平行ab,故MN不平行AB,这说明平面(AB×CD)上不可能有与MN平行的直线,因此MN与此平面不平行。
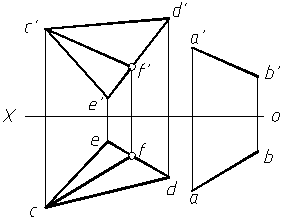
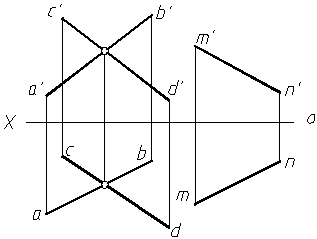
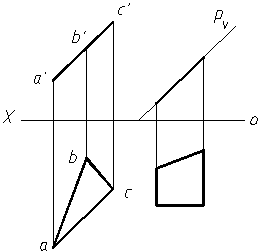
直线与某投影面垂直面平行时, 直线必有一个投影平行于该平面的积聚性投影。直线AB平行于铅垂面P, 则ab∥PH。
2.平面与平面平行
由初等几何可知,若两平面内各有一对相交直线对应地平行,则此两平面互相平行。AB∥A1B1,BC∥B1C1, 故平面(AB×BC)与平面(A1B1×B1C1)互相平行。
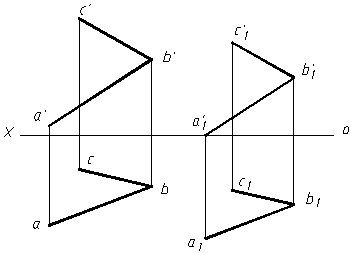
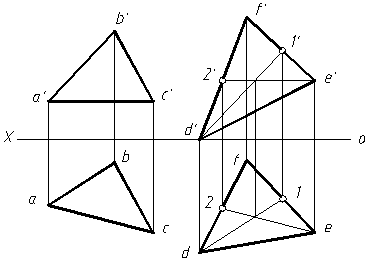
若两投影面垂直面互相平行, 则其积聚性投影互相平行,
二、相交问题
1.直线与平面相交
直线与平面相交,交点是直线与平面的共有点。直线与平面的正面投影有一段重叠,产生了遮挡问题。若交点在平面图形以内,则在投影重叠部分,直线总是以交点分界,一端可见,另一端不可见。
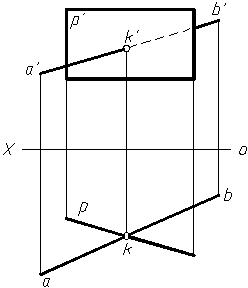
直线AB与铅垂面P相交,铅垂面P的水平投影积聚成直线段p,交点K既在平面P上,其水平投影k必在线段p上;交点K又在直线AB上,故k亦必在ab上。因此ab与p之交点k必为交点K的水平投影。而点K的正面投影k′必在a′b′上。从水平投影可以看出,直线的AK段在平面之前,BK段在平面之后。所以a′k′可见,b′k′与p′重叠部分不可见,画成虚线。
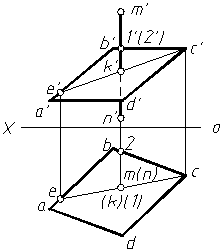
铅垂线MN与平面ABCD相交。因交点K在MN上,故k与mn重合;因点K又在平面ABCD上,故可利用平面上取点的方法,用辅助线(如CE)求出k′。直线MN正面投影的可见性,可以利用直线MN与平面上直线CD的重影点I、II来判断。从图中可以看出,MN线上的点I在前,BC线上的点II在后,故1′可见,m′k′段也可见。
2.平面和平面相交
两平面若不平行就相交,交线是一直线,是两平面的共有线。两平面的交线,可由两平面的两个共有点或一个共有点及一方向确定。当交线在平面图形的范围内时,P、Q两平面投影重叠部分,其可见性总是以交线为界,若交线的一侧为P面可见,则交线的另一侧必Q面可见。
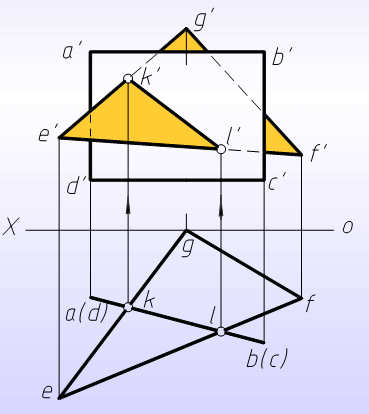
铅垂面ABCD与一般位置面EFG相交,只需求出两个共有点,就可得出交线。为此:求出EFG面上两直线EF、EG与ABCD面的交点K、L,直线KL即为两已知平面的交线。
两平面正面投影的重叠部分,交线左方三角形平面在前,故e¢k¢l¢见,a¢b¢被遮挡的一段应画成虚线;交线右方的四边形平面可见,三角形平面轮廓线被遮掩部分应画成虚线。为使图形明显起见,可在一个平面的投影的可见部分画上45°线。
一般位置平面ABCD与水平面P相交。交线KL既在平面P上,则必是水平线,且kl与p重合;交线KL又在平面ABCD上,必是该平面上的水平线,因k在c d上,且kl//bc,故k在cd上,且kl//bc。两铅垂面相交,交线应是铅垂线,其水平投影是两平面积聚性投影的共有点k(l),正面投影k¢l¢^OX。
三、垂直问题
1.直线与投影面垂直面垂直
若平面垂直于某投影面, 其垂线必平行于该投影面, 且垂线在该投影面上的投影垂直于此平面的积聚性投影。
由初等几何可知,若一直线垂直于某平面,则此直线必垂直于该平面上的一切直线。反之,若一直线垂直于某平面上二相交直线,则此直线必垂直于该平面。
由两直线投影垂直特性可得到直线与平面垂直的投影特点如下:若一直线与某平面垂直,则该直线的水平投影垂直于平面上水平线的水平投影,同时,其正面投影垂直于平面上正平线的正面投影。反过来说,在一般情况下,若一直线的水平投影垂直于平面上水平线的水平投影,同时,其正面投影垂直于平面上正平线的正面投影,则此直线与平面互相垂直。
2.直线与一般位置面垂直
直线KL垂直于平面P,必垂直于平面P上的一切直线,其中包括过垂足的水平线ⅠⅡ、正平线Ⅲ Ⅳ,以及不通过垂足的水平线AB、正平线AC。根据垂直两直线的投影可知,KL的水平投影kl垂直于12及ab,正面投影k 垂直于34及ac。
3.两平面互相垂直
由初等几何可知,如一直线垂直于某平面,则包含此直线的一切平面都与该平面垂直。反之,如两平面互相垂直,则由一平面上任一点向另一平面所作的垂线,必在前一平面上。
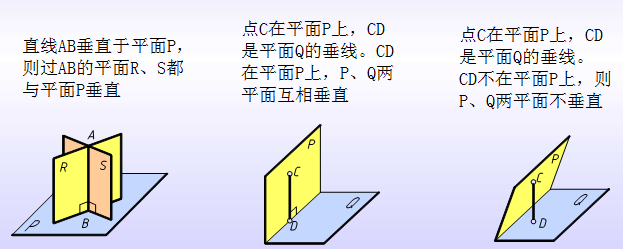
3.两平面互相垂直
举例说明。


