分析和设计任何一个控制系统，首要任务是建立系统的数学模型。

系统的数学模型是描述系统输入、输出变量以及内部各变量之间关系的数学表达式。

建立数学模型的方法分为解析法和实验法：

解析法：依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表达式，并实验验证。

解析法：依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表达式，并实验验证。

总结： 解析方法适用于简单、典型、常见的系统，而实验方法适用于复杂、非常见的系统。实际上常常是把这两种方法结合起来建立数学模型更为有效。

控制系统微分方程的建立

基本步骤：

分析各元件的工作原理，明确输入、输出量；

建立输入、输出量的动态联系；

消去中间变量；

标准化微分方程。

列写微分方程的一般方法

例：设有一弹簧质量 阻尼动力系统如图所示，当外力F(t)作用于系统时，系统将产生运动，试写出外力F(t)与质量块的位移y(t)之间的动态方程。其中弹簧的弹性系数为k，阻尼器的阻尼系数为f，质量块的质量为m。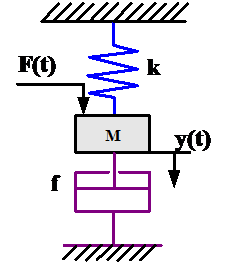

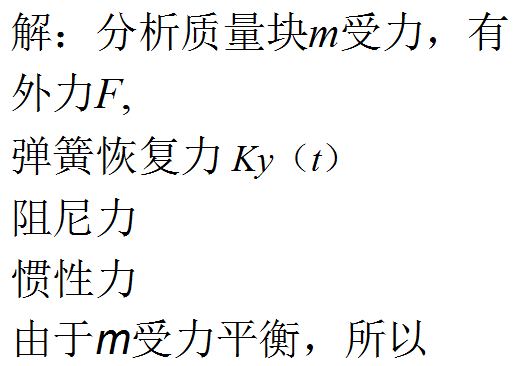
式中：Fi是作用于质量块上的主动力，约束力以及惯性力。

将各力代入上等式，则得

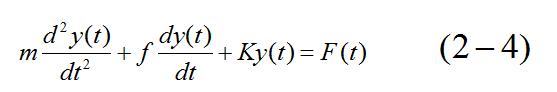
式中：y——m的位移（m）；
           f——阻尼系数（N·s/m);
           K ——弹簧刚度（N/m)。
将式(2-4)的微分方程标准化

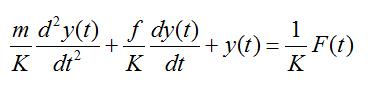
如何建立系统的数学模型？