一、方法的重载

1. 什么是方法的重载(Overload)？

方法的名称相同，但是参数列表不同。

2. 什么叫参数列表不同？

参数列表不同有下列三种情况，均可以形成重载。

• 1. 参数的个数不同
  下面两个方法的方法名相同，但参数数量不同，可以形成重载

public static int sum(int a, int b) {...}
public static int sum(int a, int b, int c) {...}

• 2. 参数的类型不同
  下面两个方法形参的类型不同，一个是int类型，一个是double类型，可以形成重载

public static int sum(int a, int b) {...}
public static double sum(double a, double b) {...}

• 3. 参数的多类型顺序不同
  下面两个方法各有两个形参，都是int和double类型，但排列顺序不同，依然可以形成方法重载

public static double sum(int a, double b) {...}
public static double sum(double a, int b) {...}

3. 重载与什么因素无关？

• 1. 与返回值类型无关
  下面两个相同方法名、不同返回值的方法无法形成重载。

public static int sum(int a, int b) {...}
public static String sum(int a, int b) {...}

为什么不能重载？假如方法有返回值，方法的调用有三种：单独调用、赋值调用和打印调用。我们可以想像，如果返回值类型不同可以重载，其中赋值调用和打印调用可以区分，但单独调用的时候我们并不使用返回值，所以无法区分！所以重载与返回值类型无关。

• 2. 与参数名称无关
  下面两个方法形参名不同，但不能形成重载，因为传参过程中使用的是参数里面的值，而不是参数是什么变量名。

public static int sum(int a, int b) {...｝
public static int sum(int x, int y) {...｝




对于一个复杂的问题，把原问题分解为如干个相对简单前类同的子问题，继续下去至到能够直接求解，也就是说到了递推的出口，这样原问题就有递推得解。 
关键要抓住的是：
    1.递归出口 
    2.递推逐步向出口逼近 

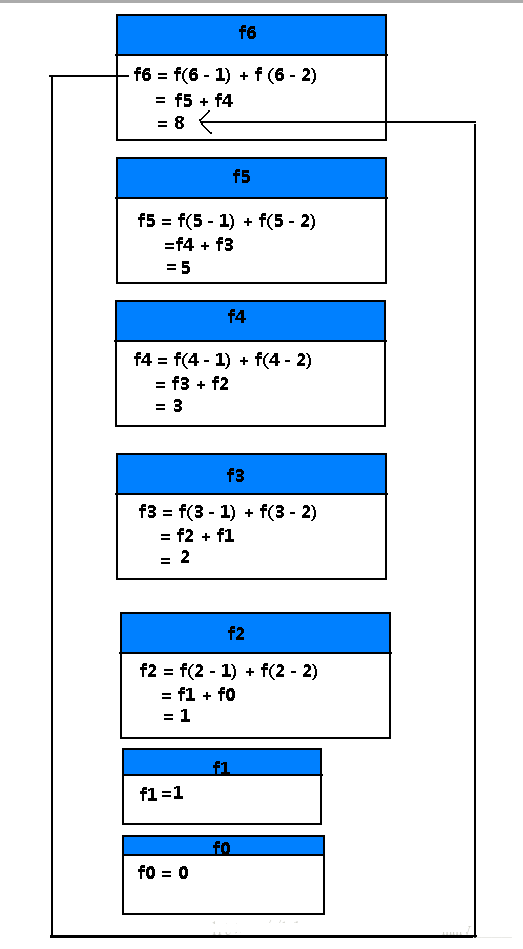
斐波纳契数列，其通项公式为：F(0)=0，F(1)=1，Fn=F(n-1) +F(n-2)（n>=3，n∈N*），现在求F(6)的值，怎么做呢？观察：这个数列从第三项开始，每一项都等于前两项之和。要求F(6)的值，肯定要先求F(5)和F(4)的值，而求F(5)的值又需要求F(4)和F(3)的值... ...解决办法1：依次求出F(1)、F(2)、F(3)、F(4)，F(5)值，再处理,如下图所示:

递归程序如下：
public class Recursion 
{
 static int fn(int n)
 {
  if(n==0)
  {
   return 0;
  }
  else if(n==1)
  {
   return 1;
  }
  else
  {
   return Recursion.fn(n-1)+Recursion.fn(n-2);
  }
 }
 public static void main(String[] args)
 {
  int result=Recursion.fn(6);
  System.out.println("fn(5)="+result);
 }
}