在学习之前，请了解一下傅里叶变换
动画图解傅里叶变换
话不多说先上两个GIF图。
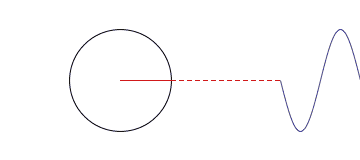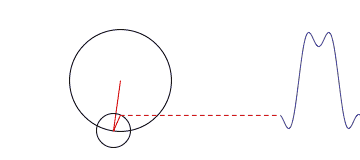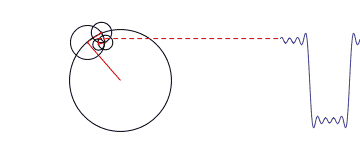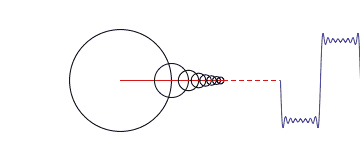
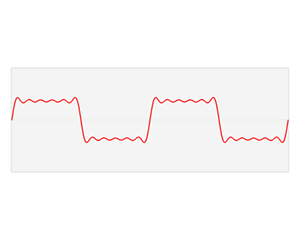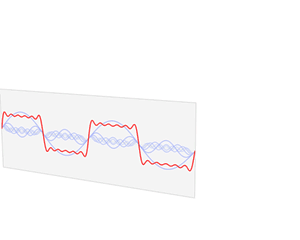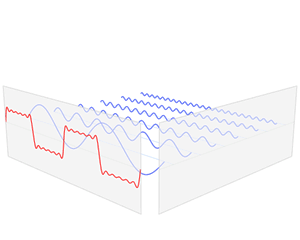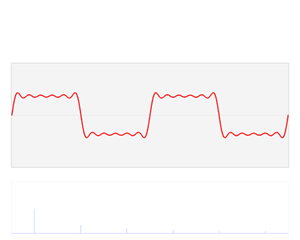
第一个动画和第二个动画其实都是对时域的周期矩形形波（近似看成矩形波，并不是严格意义的矩形方波）进行傅里叶变换分析。
对于第一个图形来说，它侧重展示变换的本质之一：叠加性，每个圆代表一个谐波分量。
第二个图形则侧重展示离散的频谱图。
但是这两个图形其实都只是展示了周期信号的频谱分析，对应的都是离散谱，而且都只是对一种很特殊的时域波形进行的分析。不过通过这两个动画，想必对傅里叶变化也有了更深刻的印象吧！
第一章 信号及其描述
在生产实践和科学实验中，需要观测大量的现象及其参量的变化。这些变化量可以通过测量装置变成容易测量、记录和分析的电信号。一个信号包含着反映被测系统的状态或特性的某些有用的信息，它是人们认识客观事物内在规律、研究事物之间的相互关系、预测未来发展的依据。这些信号通常用时间的函数（或序列）来表述该函数的图形称为信号的波形。
学习目标
完成本章内容的学习后应能做到：
1.了解信号分类方法
2.掌握信号时域和频域之间的区别与联系
3.掌握信号频谱分析方法
4.掌握周期信号与瞬变信号频谱特点
学习难点
信号的时域描述和频域描述的物理意义及时域、频域描述的互相转换。单位脉冲函数的性质及其物理意义。
内容概述
本章从不同角度说明信号的分类及其定义。介绍周期信号和非周期信号的频域描述及其频域特征，随机信号的概念和关于随机信号幅值的若干统计参数，时域—频域转换的数学工具即傅里叶变换的概念和主要性质，若干典型函数的频谱。
好了，开始学习课程
第一节 信号的分类与描述
1.1.1 信号分类
为了深入了解信号的物理实质，将其进行分类研究是非常必要的。以不同的角度来看待信号，可以将信号分为
1. 确定性信号与非确定性信号；
（1） 确定性信号
可以用明确的数学关系式描述的信号称为确定性信号。它可以进一步分为周期信号、非周期信号与准周期信号等，如下图所示。
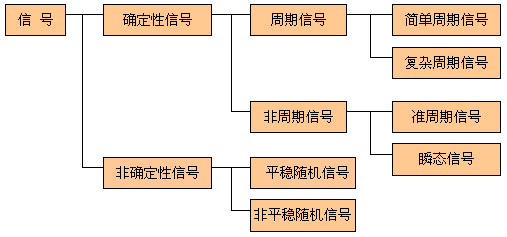
图2.1-1 信号的分类描述
周期信号是指经过一定时间可以重复出现的信号，满足条件
x ( t ) = x ( t + nT )
式中T——周期，T=2π/ω0；
。。ω0——基频； 。。n=0,±1, …。
例如，下面是一个50Hz正弦波信号10sin(2*π*50*t)的波形，信号周期为1/50=0.02秒。
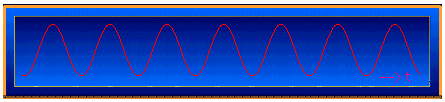
图2.1-2 50Hz正弦波信号波形
机械系统中，回转体不平衡引起的振动，往往也是一种周期性运动。例如，下图是某钢厂减速机上测得的振动信号波形(测点3)，可以近似地看作为周期信号
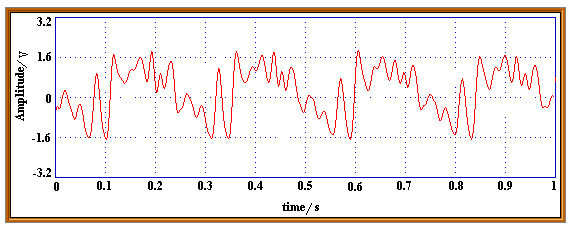
图2.1-3.4 某钢厂减速机测点3振动信号波
非周期信号是不会重复出现的信号。例如，锤子的敲击力、承载缆绳断裂时的应力变化、热电偶插入加热炉中温度的变化过程等，这些信号都属于瞬变非周期信号，并且可用数学关系式描述。例如，下图是单自由度振动模型在脉冲力作用下的响应。
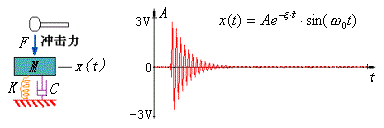
图2.1-5 单自由度振动模型脉冲响应信号波形
准周期信号是非周期信号的特例，处于周期与非周期的边缘情况，是由有限个周期信号合成的，但各周期信号的频率相互间不是公倍数关系，其合成信号不满足周期条件，例如 是两个正弦信号的合成，其频率比不是有理数，不成谐波关系。下面是其信号波形
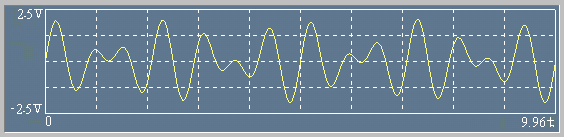
图2.1-6 准周期信号波形
这种信号往往出现于通信、振动系统，应用于机械转子振动分析、齿轮噪声分析、语音分析等场合。
(2)非确定性信号
非确定性信号不能用数学关系式描述，其幅值、相位变化是不可预知的，所描述的物理现象是一种随机过程。随机信号具有某些统计特征，可以用概率统计方法由其过去来估计其未来。随机信号所描述的现象是随机过程。自然界中有许多随机过程，例如，汽车奔驰时所产生的振动、飞机在大气流中的浮动、树叶随风飘荡、环境噪声等。
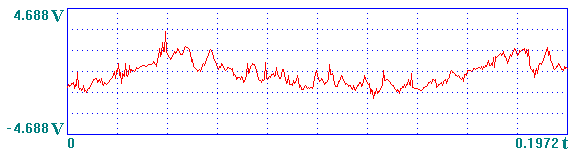
图2.1-7 加工过程中螺纹车床主轴受环境影响的振动信号波形
随机过程有平稳过程和非平稳随机过程之分。所谓平稳随机过程是指其统计特征参数不随时间而变化的随机过程，否则为非平稳随机过程。在平稳随机过程中，若任意单个样本函数的时间平均统计特征等于该过程的几何平均统计特征，这样的平稳随机过程叫各态历经（遍历性）随机过程。
然而，必须指出的是，实际物理过程往往是很复杂的，既无理想的确定性，也无理想的非确定性，而是相互参杂的。
2. 连续时间信号与离散时间信号
连续时间信号：在所讨论的时间间隔内，对于任意时间值(除若干个第一类间断点外)都可给出确定的函数值，此类信号称为连续时间信号或模拟信号。连续信号的幅值可以是连续的也可以是不连续的，但独立变量（时间）取值是连续的。若时间变量和幅值均为连续的信号称为模拟信号。
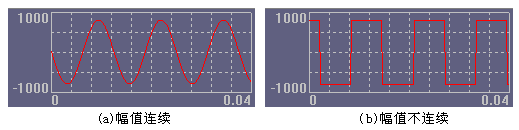
图2.1-8连续信号
离散时间信号：离散时间信号在时间上是离散的。只是在某些不连续的规定瞬时给出函数值，而在其它时间没有定义的信号。 离散信号又可分为两种：时间离散而幅值连续的信号称为采样信号；时间离散且幅值离散（量化）的信号称为数字信号。
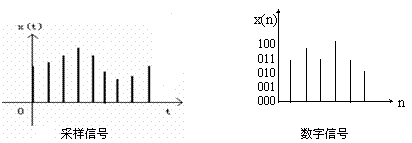
图2.1-9 离散时间信号
3.能量信号与功率信号
1)能量信号
在所分析的区间（-∞，∞），能量为有限值的信号称为能量信号，满足条件
关于信号的能量，可作如下解释：对于电信号，通常是电压或电流，电压在已知区间（t1，t2）内消耗在电阻上的能量.
对于电流，能量
在上面每一种情况下，能量都是正比于信号平方的积分。讨论消耗在电阻上的能量往往是很方便的，因为当R=1Ω时，上述两式具有相同形式，采用这种规定时，就称方程
为任意信号x(t) 的“能量”。如矩形脉冲信号、衰减指数函数等均为能量信号
(2)功率信号
有许多信号，如周期信号、随机信号等，它们在区间（-∞，∞）内能量不是有限值。在这种情况下，研究信号的平均功率更为合适。在区间（t1，t2）内，信号的平均功率
若区间变为无穷大时，上式仍然是一个有限值，信号具有有限的平均功率，称之为功率信号。具体讲，功率信号满足条件
一般持续时间无限的信号都属于功率信号:
对比上式，显而易见，一个能量信号具有零平均功率，而一个功率信号具有无限大能量。
1.1.2、信号的时域和频域描述
信号作为一定物理过程（现象）的表示，它包含着丰富的信息，为了从中提取某种有用信息，需要对信号进行必要的分析和处理，以全面了解信号的特性。所谓信号分析就是采用各种物理的或数学的方法提取有用信息的过程，而信号的描述方法提供了对信号进行各种不同变量域的数学描述，表征了信号的数据特征，它是信号分析的基础。通常以四个变量域来描述信号，即时间域（简称时域）、频率域（简称频域）、幅值域和时延域。
以时间作为自变量的信号表达，称为信号的时域描述。时域描述是信号最直接的描述方法，它反映了信号的幅值随时间变化的过程，从时域描述图形中可以知道信号的时域特征参数，即周期、峰值、均值、方差、均方值等。它们反映了信号变化的快慢和波动情况，因此时域描述比较直观、形象、便于观察和记录，用示波器、万用表等普通仪器就可以进行分析。
以信号的频率作为自变量的信号表达，称为信号的频域描述。信号的频域描述可以揭示信号的频率结构，即组成信号的各频率分量的幅值、相位与频率的对应关系，因此在动态测试技术中得到广泛应用。
信号的幅值域描述是以信号幅值为自变量的信号表达方式，它反映了信号中不同强度幅值的分布情况，常用于随机信号的统计分析。由于随机信号的幅值具有随机性，通常用概率密度函数来描述，概率密度函数反映信号幅值在某一范围内出现的概率，提供了随机信号沿幅值域分布的信息，它是随机信号的主要特征参数之一。
以时间和频率的联合函数来同时描述信号在不同时间和频率的能量密度或强度，称为信号的时延描述。它是非平稳随机信号分析的有效工具，可以同时反映其时间和频率信息，揭示非平稳随机信号所代表的被测物理量的本质，常用于图像处理、语音处理、医学、故障诊断等信号分析中。
信号的各种描述方法是从不同的角度观察和描述同一信号，并不改变信号的实质，它们之间可通过一定的数学关系进行转换，例如傅立叶变换可以将信号描述从时域转换到频域，而傅立叶反变换可以从频域转换到时域。
信号的时域描述
直接观测或记录到的信号，一般是以时间为独立变量的，称其为信号的时域描述。信号的时域描述能反映信号幅值随时间变化的关系。
信号时域分析(波形分析)的一个重要功能是根据信号的分类和各类信号的特点确定信号的类型。然后再根据信号类型选用合适的信号分析方法。
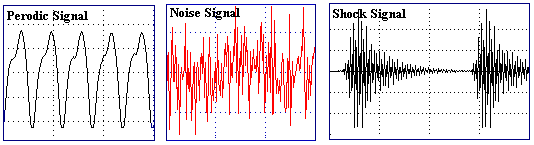
(a) periodic signal 周期信号 (b)噪声信号 (c)打击信号
图2.1-11 三种不同特征的信号
时域波形分析的应用：信号的类型识别、信号的基本参数识别、超门限报警。
信号的频域描述
信号的时域描述能反映信号幅值随时间变化的关系，而不能明显解释信号的频率组成关系。为了研究信号的频率结构和各频率成分的幅值、相位关系，应对信号进行频谱分析，把信号的时域描述通过适当方法变成信号的频域描述，即是以频率为独立变量来表示信号。信号的频域描述在动态测试技术中得到广泛应用。
图2.1-11是一个周期方波的一种时域描述，而式(1.3-1)则是其时域描述的另一种形式
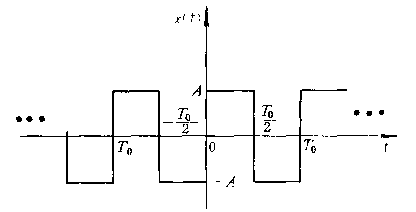
图2.1-11 周期方波
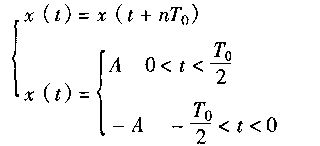（1.3-1）
若该周期方波应用傅里叶级数展开，即得
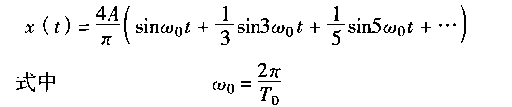(1.3-2)
由式(1.3-2)得，该周期方波是由一系列幅值和频率不等、相角为零的正弦信号叠加而成的。此式除t之外尚有另一变量ω为各正弦成分的频率。若视t为参变量，以ω为独立变量，则此式即为该周期方波的频率描述。
在信号分析中，将组成信号的各频率成分找出来，按序排列，得到信号的“频谱”。若以频率为横坐标、分别以幅值或相位为纵坐标，便分别得到信号的幅值谱或相频谱。图1.3.2-2示出了该周期方波的时域图形、幅值谱和相频谱三者的关系。
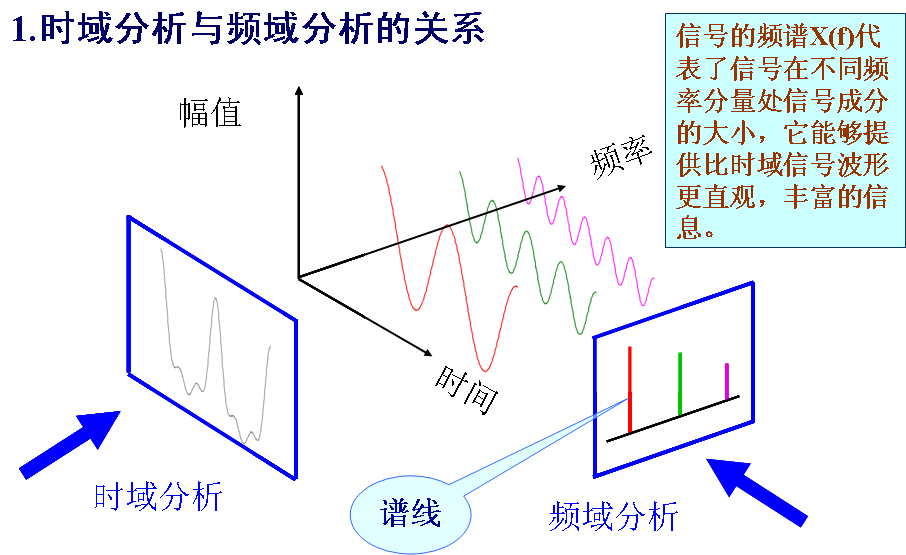
图2.1-12 周期方波的描述
信号时域描述直观地反映出信号瞬时值随时间变化的情况；频域描述则反映信号的频率组成及其幅值、相角之大小。为了解决不同问题，往往需要掌握信号不同方面的特征，因而可采用不同的描述方式。例如，评定机器振动烈度，需用振动速度的均方根值来作为判据。若速度信号采用时域描述，就能很快求得均方根值。而在寻找振源时，需要掌握振动信号的频率分量，这就需采用频域描述。实际上，两种描述方法能相互转换，而且包含同样的信息量。
