第二节 周期信号与离散频谱
本节从周期信号的频域描述开始，运用数学方法，逐一介绍不同信号的描述方法及其应用。信号频谱分析是采用傅里叶变换将时域信号x(t)变换为频域信号X(f)，从而帮助人们从另一个角度来了解信号的特征。
1.2.1 傅里叶级数的三角函数展开式
周期信号是经过一定时间后可以重复出现的信号，满足条件：
x (t) = x (t + nT)
从数学分析已知，任一周期信号x (t) 在有限区间（t，t+T）上满足狄里赫利条件时，即①信号在定义周期[0，T]内单调连续或只有有限个第一类间断点；②在此定义周期内只有有限个极限点；③x (t)是绝对可积；则信号x (t)可以展开成傅立叶级数。傅立叶级数有两种表达式，即三角函数展开式和复指数函数展开式。
三角函数形式
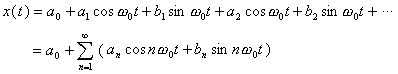(1.4-6) 式中ω0——周期信号基频的角频率；T——信号周期；a0，an，bn——傅立叶系数；
直流分量幅值为
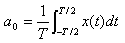
各余弦分量幅值为
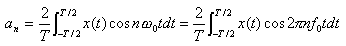
各正弦分量幅值为
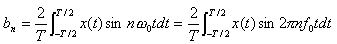
利用三角函数的和差化积公式，周期信号的三角函数展开式还可以写为下面的形式
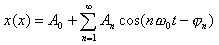（1.4-10）
直流分量幅值为
各频率分量幅值为
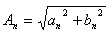
各频率分量的相位为
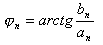
式中n=0,±1, …；
式中an,bn,An,n—为信号的傅里叶系数，表示信号在频率fn处的成分大小。
式（1.4-6）和（1.4-10）实际描述了周期信号x(t)的频率结构，表明周期信号是由一个常值分量a0和无穷多个不同频率的谐波分量叠加而成的。
由于n是整数序列，当n=1时
称为一次谐波分量（基波），基波的频率与信号的频率相同；当n＞1时，
称为n次谐波，各高次谐波分量的频率都是
的整数倍
以频率ω为横坐标，以各次谐波的幅值An或相角
为纵坐标分别作图，则可以得到该信号的幅频谱图和相频谱图，横坐标的取值范围为0～＋∞。
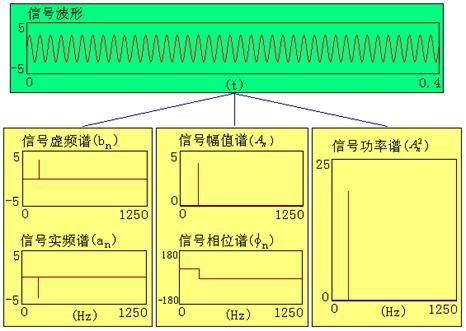
图2.1-13 信号的频谱表示
举例，图2.1-11周期方波信号的频谱
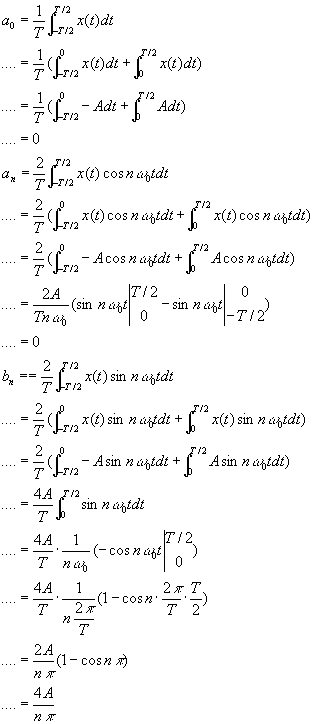
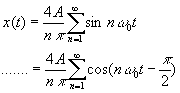
其波形、幅值谱和相位谱分别如下图所示。
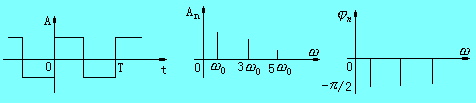
图2.1-14 方波信号的波形、幅值谱和相位谱
周期信号的频谱特点
由以上可知周期信号的频谱特点：
（1）离散性：周期信号的频谱是离散谱；
（2）谐波性：周期信号的频率成分是基频的整数倍；
（3）收敛性：满足狄里赫利条件的周期信号，其谐波幅值总的趋势是随谐波频率的增大而减小。
1.2.2 傅里叶级数的复指数函数展开式
根据欧拉公式
（1-6）
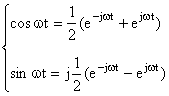（1-7）
将式（1-7）带入公式（1-6）可得
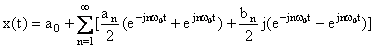
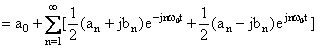
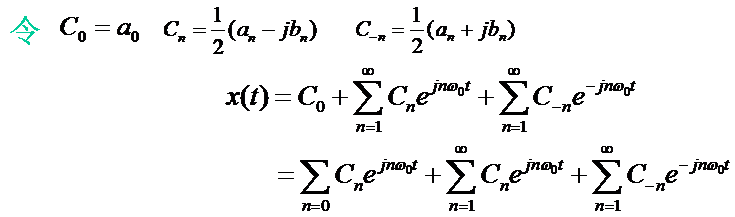
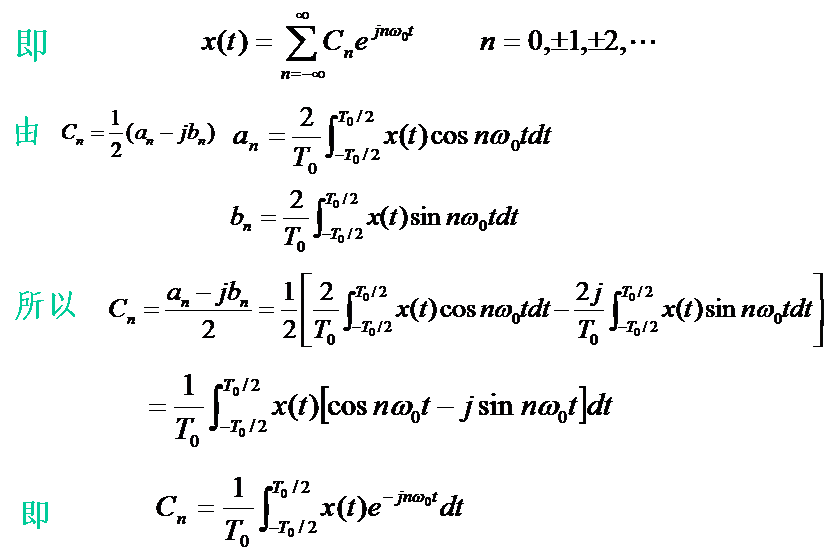
举例说明：
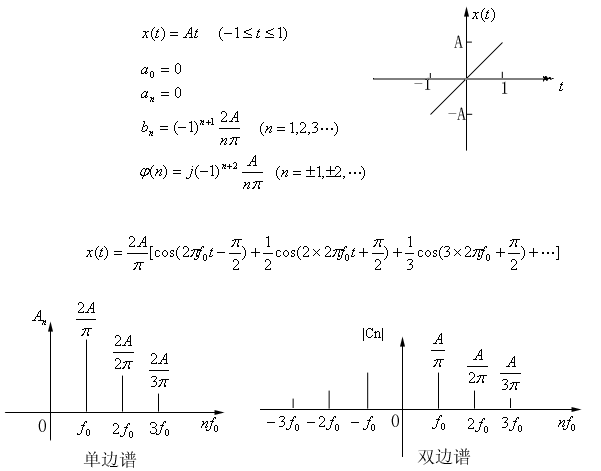
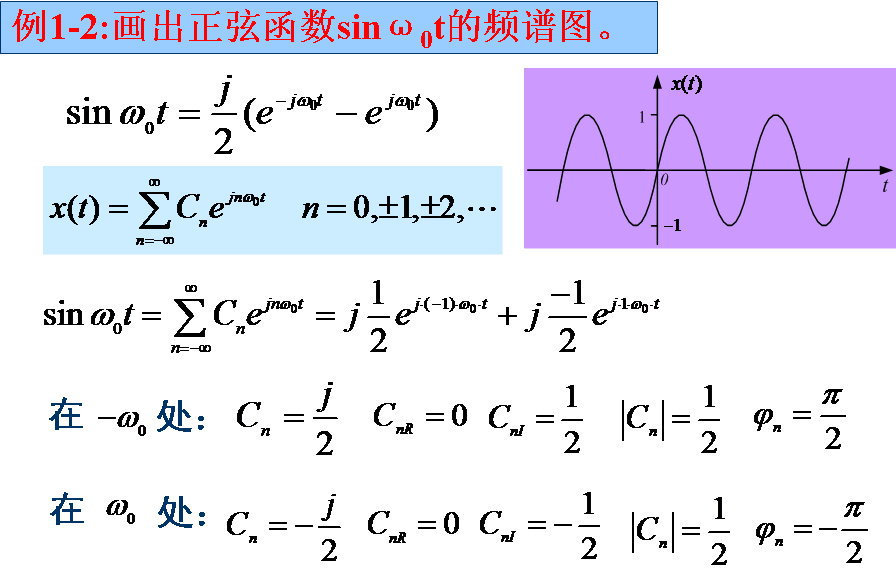
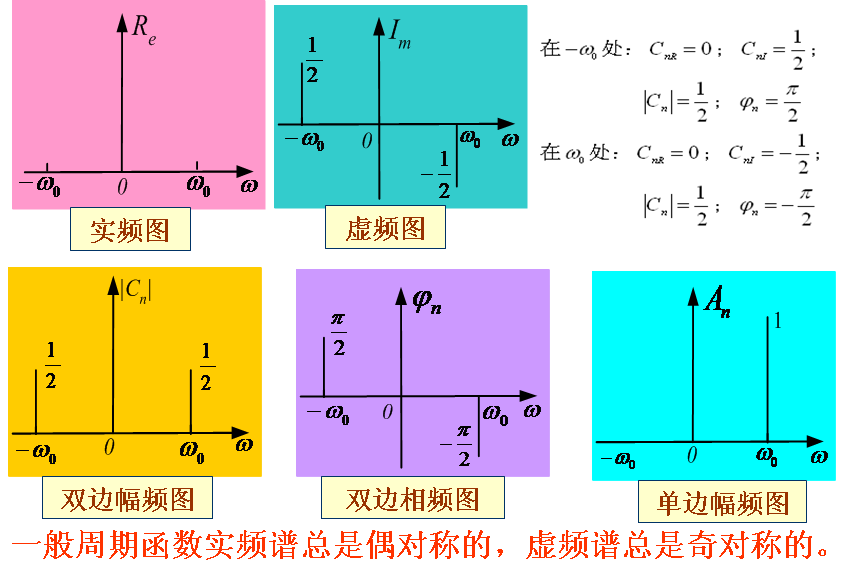
4.傅立叶级数复指数与三角函数展开的关系
比较傅里叶级数的两种展开形式可知：
l 复指数函数形式的频谱为双边谱（ω从-∞到+∞）；
l 三角函数形式的频谱为单边谱（ω从0到+∞）；
l 两种频谱各谐波幅值在量值上有确定的关系、
周期信号频域描述的物理意义
任何一个周期信号x(t)只要满足狄里赫利条件，就可以展开成三角函数形式或复指数函数形式的傅立叶级数，表明周期信号x(t)必定是由有限个或无穷多个谐波分量叠加而成，这一结论对于工程测试非常重要。
当一个复杂的周期信号x(t)作用到一线性测试系统时，测量其输出信号就可以把这个复杂周期信号的作用看成是若干个简谐信号叠加作用的结果，从而使问题简化。另外，在工程测试系统中，常常包含许多测量装置，如传感器、放大器、滤波器等，而任何一个测量装置的工作频带宽度都是有限的，输入信号中高次谐波的频率如果超过了测量装置的截止频率，这些高次谐波就得不到放大等调理，从而引起失真，造成测量误差。可见，分析信号的频率结构对动态测试是非常重要的。
通过傅立叶级数及其表达图形——频谱图，可以一目了然地知道周期信号是由哪些频率成分构成、各频率成分的幅值和相位角是多大、各次谐波的幅值在周期信号中所占的比例等等，这些统称为周期信号的频率描述。
1.2.3 周期信号的强度描述
周期信号的强度可以峰值、绝对均值、有效值和平均功率来表述。
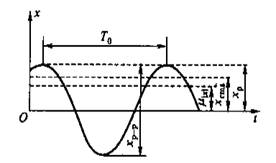
图2.1-15 周期信号的强度描述
1．峰值xp是信号在一个周期内可能出现的最大瞬时值，即
峰—峰值xp-p是在一个周期内最大瞬时值与最小瞬时值之差。对信号的峰值和峰—峰值应有足够的估计，以便确定测试系统的动态范围。一般希望信号的峰—峰值在测试系统的线性范围内，以保证足够小的非线性误差，并使信号不致产生大的畸变。
2．均值μx是信号的常值分量（直流分量），即一个周期内的平均值，表达式为：
是周期信号全波整流后的绝对均值，其表达式为:
均值又或称之为直流分量，表达了信号变化的中心趋势。
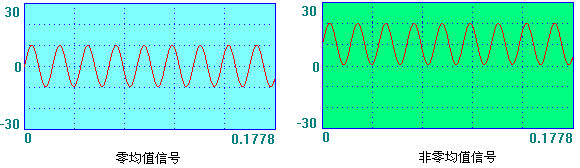
3. 有效值是信号的均方根值xrms，即
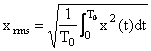
4．平均功率Pav是信号的均方值——有效值的平方，即
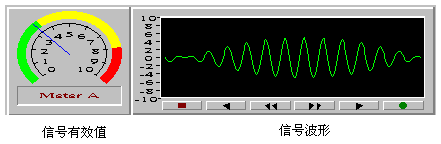
下面给出几种典型周期信号的强度。从表中可以看出，虽然信号的峰值相同，但信号的均值、绝对均值和有效值随波形不同而异。
示例:
常见周期信号的强度描述
