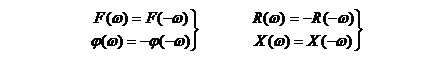第三节  瞬变非周期信号与连续频谱

非周期信号包括准周期信号和瞬态信号两种，其频谱各有独自的特点：周期信号的频谱具有离散性，各谐波分量的频率具有一个公约数——基频。但几个简谐具有离散频谱的信号不一定是周期信号。只有各简谐成分的频率比是有理数，它们才能在某个时间间隔后周而复始，合成的信号才是周期信号。若各简谐信号的频率比不是有理数，合成信号就不是周期信号，而是准周期信号。因此准周期信号具有离散频谱，例如多个独立激振源激励起某对象的振动往往是这类信号对于瞬态信号，不能直接用傅立叶级数展开，而必须应用傅立叶变换的数学方法进行分解。

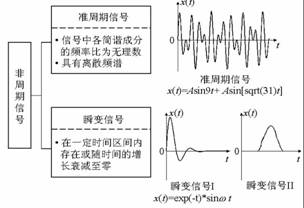
瞬变非周期信号:持续时间有限的信号（除准周期信号之外的其他非周期信号，是一些或在一定时间区间内存在，或随着时间的增长而衰减至零的信号）       

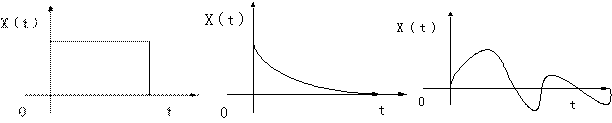                矩形脉冲信号               指数衰减信号               衰减振荡信号

1.3.1 傅里叶变换

对于非周期信号的理解：

由前面分析得，周期为T₀的信号x(t)其频谱是离散的。当x(t)的周期T₀→∞时，该信号就变成非周期信号了。对应的，周期信号频谱谱线的频率间隔△ω=ω₀=2π/T₀→0，谱线无限靠近，变量连续取值以致离散谱线的顶点最后演变成一条连续曲线。所以非周期信号的谱线是连续的。可以将非周期信号理解为无限多个、频率无限接近的频率成分所组成。

非周期信号的频谱分析

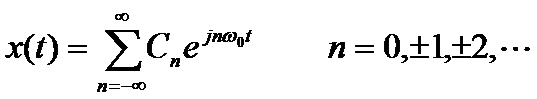
非周期信号x(t)的傅里叶变换X(f)是复数，所以有

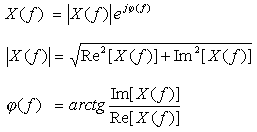
式中|X(f)|——信号在频率f处的幅值谱密度；

——信号在频率f处的相位差。

工程上习惯将计算结果用图形方式表示，以f为横坐标，Re[X(f)]、Im[X(f)]为纵坐标画图，绘出的曲线图称为时频－虚频密度谱图；以f为横坐标，|X(f)|、φ(f)为纵坐标画图，绘出的曲线图称为幅值－相位密度谱。以f为横坐标，|X(f)|²为纵坐标画图，绘出的曲线图称为功率密度谱，如下图所示。  

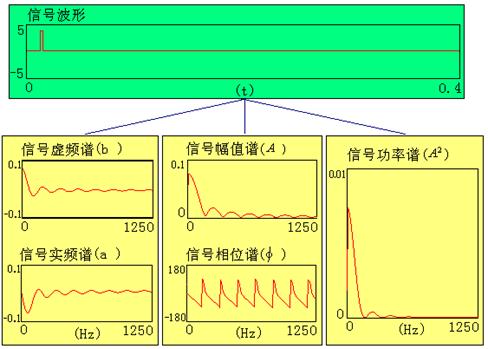
非周期信号频谱的特点：

1）非周期信号可分解成许多不同频率的正弦、余弦分量之和，但它包含了从零到无穷大的所有频率分量；
      2）非周期信号的频谱是连续的；
      3）非周期信号的频谱由频谱密度函数来描述，表示单位频宽上的幅值和相位（即单位频宽内所包含的能量）；
      4）非周期信号频域描述的数学基础是傅立叶变换。

1.3.2 傅里叶变换的性质与应用

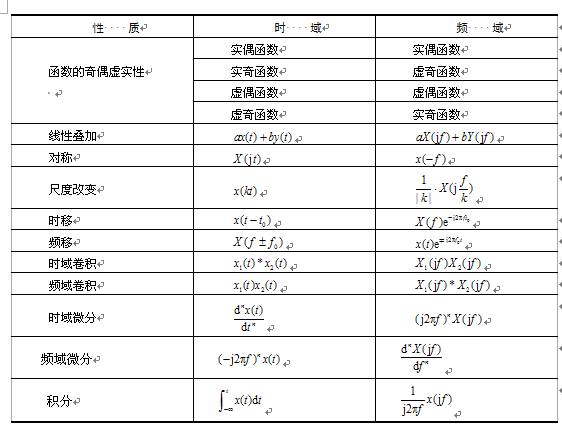
信号的时域、频域分析，以不同的角度揭示了信号的物理特性，傅立叶变换建立起它们之间的联系。作信号分析时，当在时域分析变得很困难时，可通过傅立叶变换到频域分析，使之变得简单明了。因此掌握傅立叶变换性质，有助于我们对信号分析、变换有更深刻的理解。表1-3列出了傅立叶变换的主要性质，下面就几项主要性质作一些必要的说明.

                                  表1-3  傅里叶变换的主要性质

一、        线性

傅里叶变换是一种线性运算。若

则           

其中a和b均为常数，它的证明只需根据傅里叶变换的定义即可得出。

例2-6  利用傅里叶变换的线性性质求单位阶跃信号的频谱函数。

解      因       

由式(2-55)得

二、对称性

若                     

证明   因为        

有                      

将上式中变量换为x，积分结果不变，即

再将t用代之，上述关系依然成立，即

最后再将x用t代替，则得

所以           

证毕     

若是一个偶函数，即，相应有，则式(2-56)成为

可见，傅里叶变换之间存在着对称关系，即信号波形与信号频谱函数的波形有着互相置换的关系，其幅度之比为常数。式中的表示频谱函数坐标轴必须正负对调。例如

例2-7若信号的傅里叶变换为

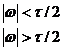
试求。

解    将中的换成t，并考虑为的实函数，有

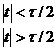
该信号的傅里叶变换由式(2-54)可知为

根据对称性            

故                     

再将中的换成t，则得

为抽样函数，其波形和频谱如图2-20所示。

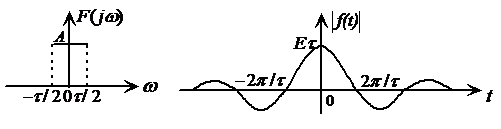
三、折叠性

若                 

则   

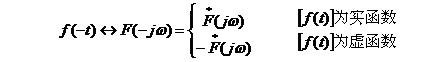
四、尺度变换性 观看动画

若                    

则        

证明  因a＞0，由

令，则，代入前式，可得

函数表示沿时间轴压缩(或时间尺度扩展) a倍，而则表示沿频率轴扩展(或频率尺度压缩) a倍。

该性质反映了信号的持续时间与其占有频带成反比，信号持续时间压缩的倍数恰好等于占有频带的展宽倍数，反之亦然。

例2-8已知

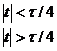
,求频谱函数。

解  前面已讨论了

的频谱函数，且

根据尺度变换性，信号比的时间尺度扩展一倍，即波形压缩了一半，因此其频谱函数

两种信号的波形及频谱函数如图2-21所示。

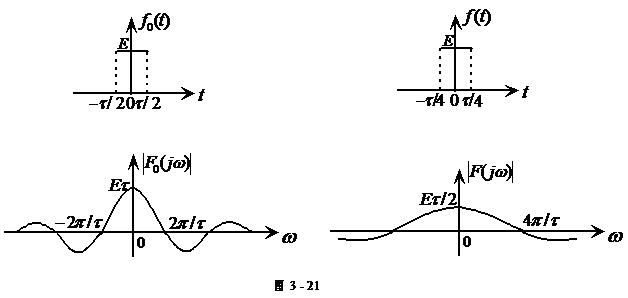
五、时移性

若                     

则                        

此性质可根据傅里叶变换定义不难得到证明。它表明若在时域平移时间，则其频谱函数的振幅并不改变，但其相位却将改变。

例2-9  求       的频谱函数。

解:  根据前面所讨论的矩形脉冲信号和傅里叶变换的时移性，有

六、频移性

若                   

则                      

证明

 证毕

频移性说明若信号乘以，相当于信号所分解的每一指数分量都乘以，这就使频谱中的每条谱线都必须平移，亦即整个频谱相应地搬移了位置。频谱搬移技术在通信系统得到了广泛应用，诸如调幅、同步解调、变频等过程都是在频谱搬移的基础上完成的。频谱搬移实现原理是将信号乘以所谓载频信号或，即

七、时域微分性

若                    

则                        

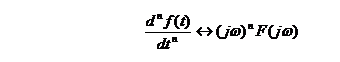
证明    因为         

两边对t求导数，得

所以                     

同理，可推出

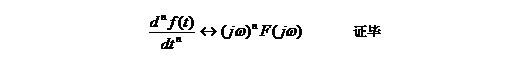
例2-10求的频谱函数。

解:  因为                 

由时域微分性                  

例2-11图2-22所示信号为三角形函数

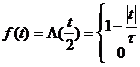
求其频谱函数。

解:  将微分两次后，得到图2-22(c)所示函数，其表达式为

由微分性

所以          

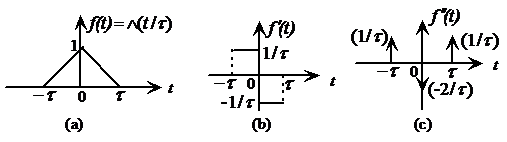
八、频域微分性

若                  

则                      

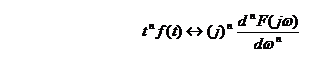
例2-12  求的频谱函数。

解:  因为           

根据频域微分性

九、时域积分性

若                      

则                  

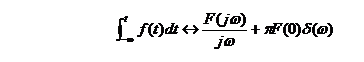
例2-13根据和积分性求的频谱函数。

解:  因为               

又                          

根据时域积分性

例2-14求图2-23所示信号的频谱函数。

解:  对求两次微分后，得

且                  

由时域积分性

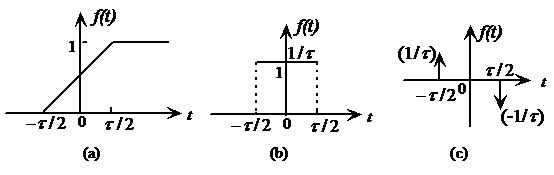
十、频域积分性

若                      

则                

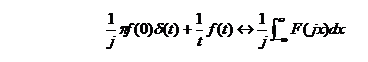
例2-15  已知，求。

解:  因为

根据频域积分性

十一、时域卷积定理

若         

则                

证明

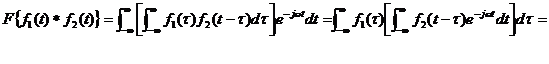
例2-16 图2-24(a)所示的三角形函数

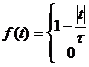
可看做为两个如图2－24(b)所示门函数卷积。试利用时域卷积定理求其频谱函数。

解：　因            

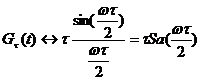
又                      

所以                    

例2-17一个信号的希伯特变换是和的卷积，即

解：  因为         

则对称性              

有                    

由时域卷积定理

即                    

十二、频域卷积定理

若           

则              

或               

例2-18  利用频域卷积定理求的傅里叶变换。

解： 因为         

由对称性              

有                     

所以根据频域卷积定理

有

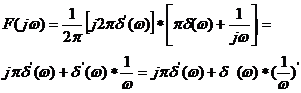
即            

十三、帕塞瓦尔定理

若                   

则             

可推广        

若为实函数，则

若,为实函数，则

例2-19求。

解： 因       

又               

由帕塞瓦尔定理可得

十四、奇偶性

若，则

(1) 当为实函数时，则

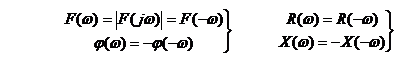
若为实偶函数，即，则

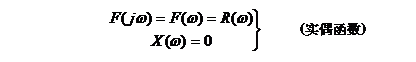
若为实奇函数，即，则

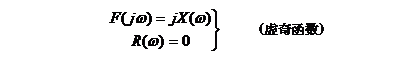
(2) 当为虚函数，即时，则