2.3 测试系统的动态响应特性

动态特性:输入量随时间作快速变化时，测试系统的输出随输入而变化的关系。

在对动态物理量进行测试时，测试系统的输出变化是否能真实地反映输入变化，则取决于测试系统的动态响应特性。

用特定的输入信号作用于测试系统，测量输出 (已知)，由此推断系统的传输特性。 (系统辨识)

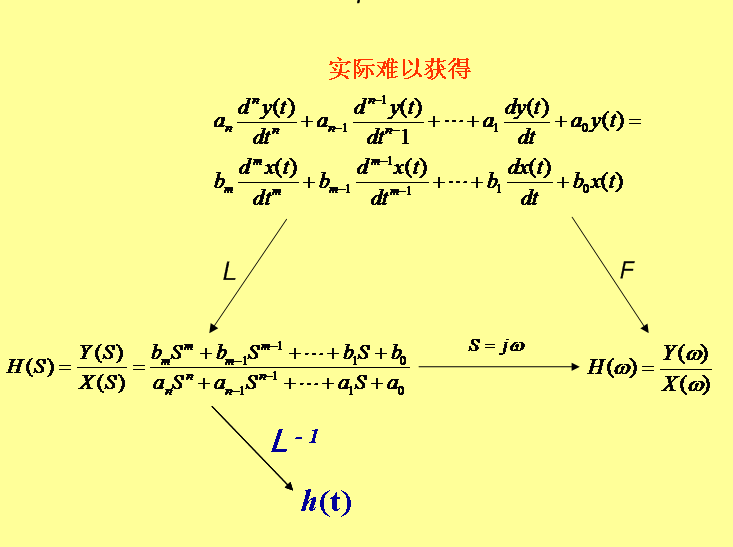
测试系统的数学模型—动态特性的决定因素

式中，、…、和、…、均为与系统结构参数有关但与时间无关的常数。 

传递函数 (Transfer function)

条件：①线性系统的初始状态零  ②x(t)↔ X(S), y(t)↔ Y(S)

进行拉普拉斯变换：

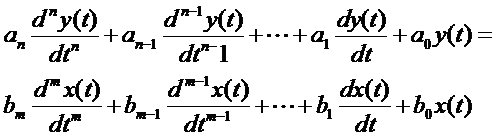
得：

系统的传递函数H(S)：

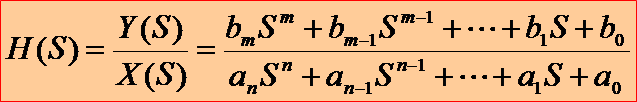
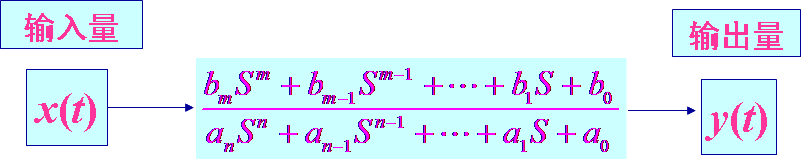
其中，S为复变量，S=α+jω； n代表微分方程的阶数；如n=1,n=2就分别称为一阶或二阶系统。

H(S)只反映系统对输入的响应特性，与测量信号无关，与具体的物理结构无关。    

H(S)中的分母完全由系统的结构所决定，分母中最高次幂n代表系统微分方程的阶数。而分子则与激励点位置、激励方式、所测量的变量以及测量点布置情况有关 。

H(S)以测试系统本身的参数表示出输入与输出之间的关系，所以它将包含着联系输入量与输出量所必须的单位

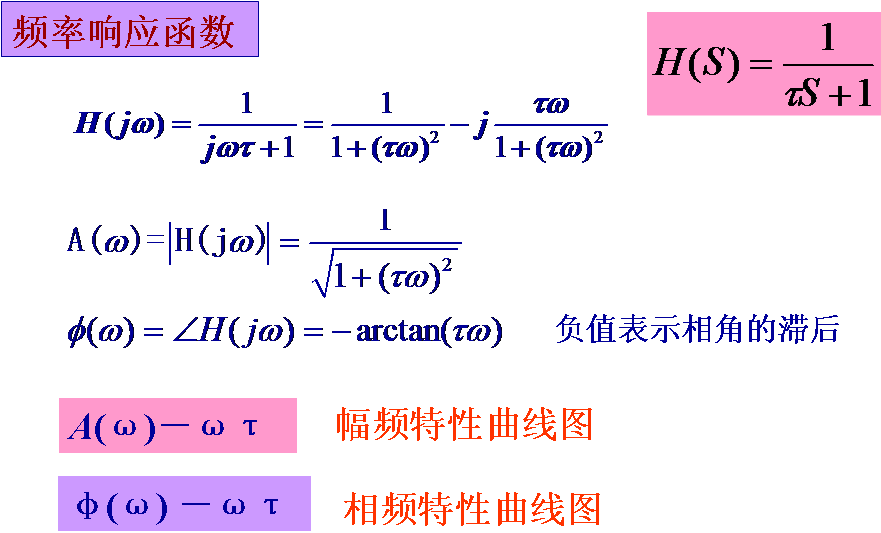
2. 频率响应函数 (Frequency response function)以   代入H(s)得：

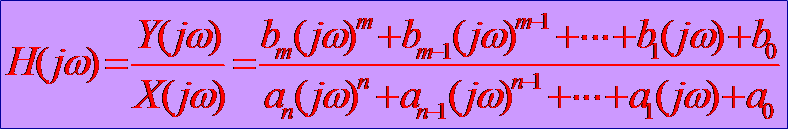
频率响应函数是传递函数的特例

(1).幅频特性

定常线性系统在简谐信号的激励下，其稳态输出信号和输入信号的幅值比 ，记为A(ω)；

(2).相频特性

H(jw)一般为复数，写成实部和虚部的形式：

其中：

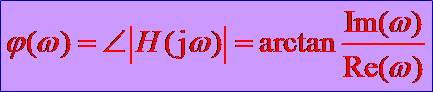
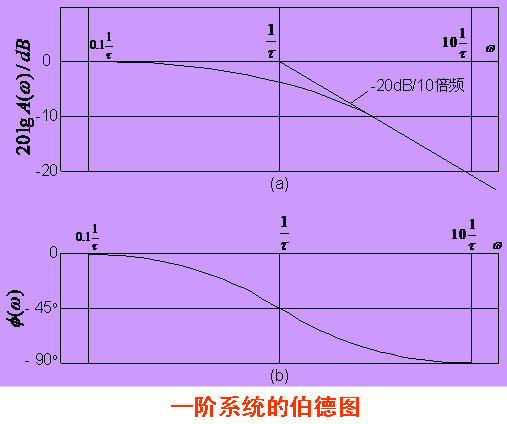
在工程应用技术中，对于幅频特性曲线和相频特性曲线的纵坐标、横坐标除了取线性标尺外，还常对自变量ω取对数标尺，幅值取分贝数，画出的20lgA(ω)-lgω曲线和φ(ω)-lgω曲线，分别称为对数幅频特性曲线和对数相频特性曲线，两种曲线总称为伯德(Bode)图 。

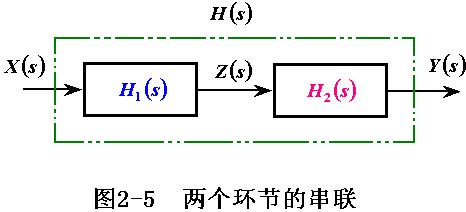
如图2-5所示，两个环节之间没有能量交换，则串联后所组成的系统的传递函数在初始条件为零时为：

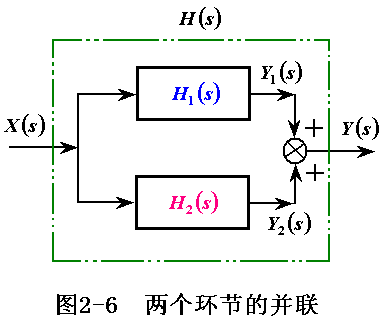
若两个环节并联（如图2-6），有

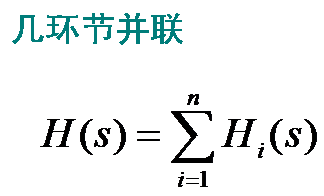
6.系统描述方法的比较

一阶、二阶系统的频率响应特性

㈠、一阶系统 输入、输出关系用一阶微分方程来描述，包括液柱式温度计，RC滤波电路，弹簧、阻尼振子

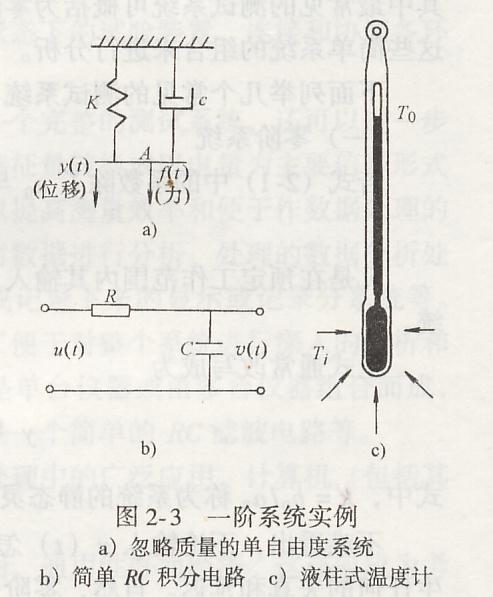
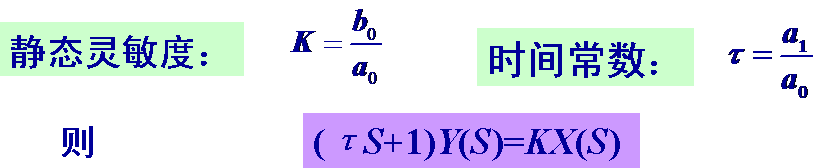
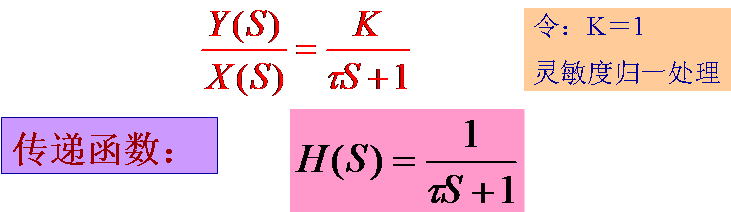
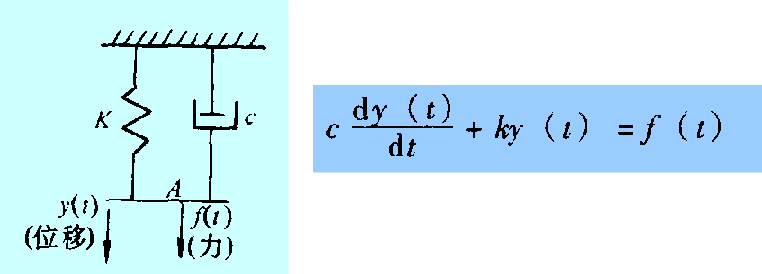
请观看一阶系统动态特性的演示动画（请用鼠标点击观看）

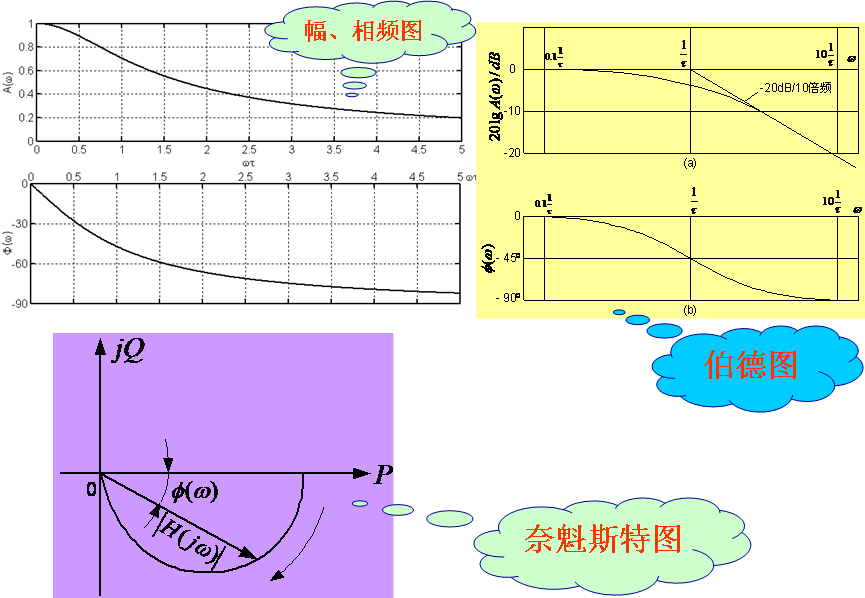
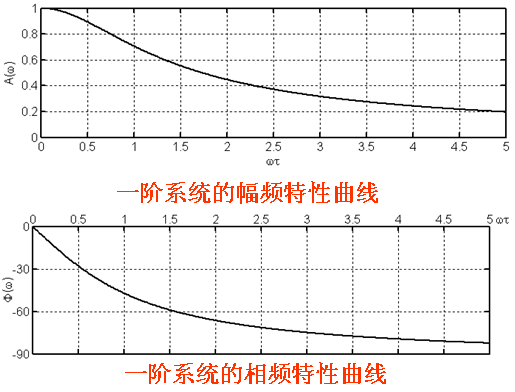
从图中可以看出，一阶系统具有以下特点:
1）一阶系统是一个低通环节，当ω＝0时，幅值比A(ω)=1为最大，相位差，其幅值误差与相位误差为零，即输出信号与输入信号的幅值、相位相同，测试系统输出信号并不衰减。随着ω的增大，A(ω)逐渐减小，相位差逐渐增大，当ω→∞时，A(ω)几乎与频率成反比，，这表明测试系统输出信号的幅值衰减加大，相位误差增大，因此一阶系统适用于测量缓变或低频信号。
通常定义系统的幅值误差为：

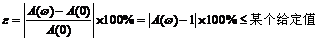
2）时间常数τ决定着一阶系统适用的频率范围。当较小时，幅值和相位的失真都较小；当时，，即20lgA(ω)＝－3dB。通常把处的频率（即输出幅值下降至输入幅值的0.707倍处的频率）称为系统的“转折频率”（对滤波器来讲，就是截止频率），在该处相位滞后45°。
　　可以看出，τ越小转折频率就越大，测试系统的动态范围越宽，反之，τ越大则系统的动态范围就越小。因此，τ是反映一阶系统动态特性的重要参数。
　　因此，为了减小一阶系统的稳态响应动态误差，增大工作频率范围，应尽可能采用时间常数τ小的测试系统。

例 2.3: 用一个一阶系统作100Hz正弦信号测量。(1)如果要求限制振幅误差在5%以内，则时间常数    应取多少？(2)若用具有该时间常数的同一系统作50Hz信号的测试，此时的振幅误差和相角差各是多少？

         
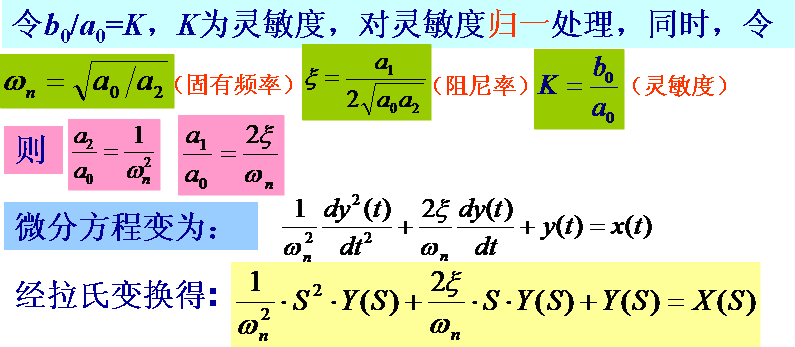
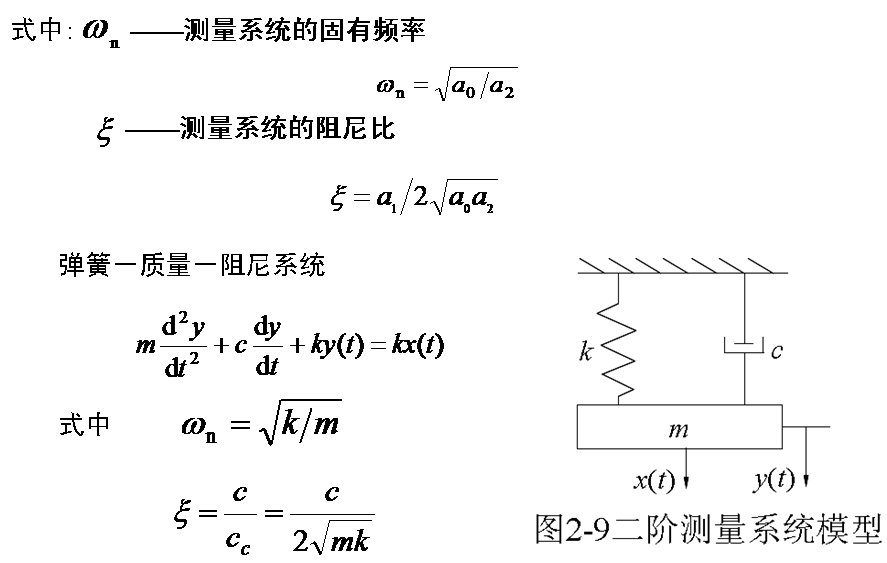
    请看二阶系统幅频特性的动画（点击鼠标观看）               

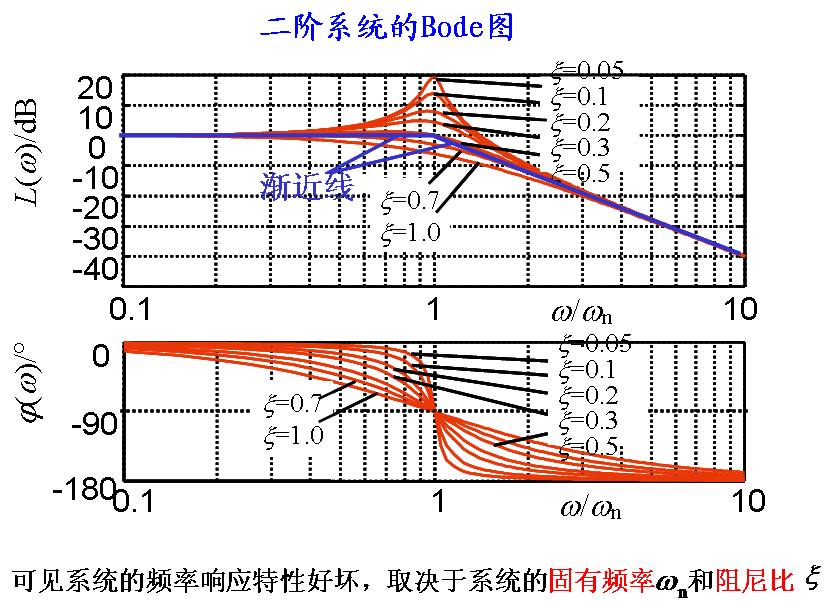
由图可知，二阶系统具有以下特点：