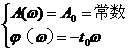2.4 实现不失真测量的条件

设测试系统的输出y(t)与输入x(t)满足关系: y(t)=A0x(t-t0)

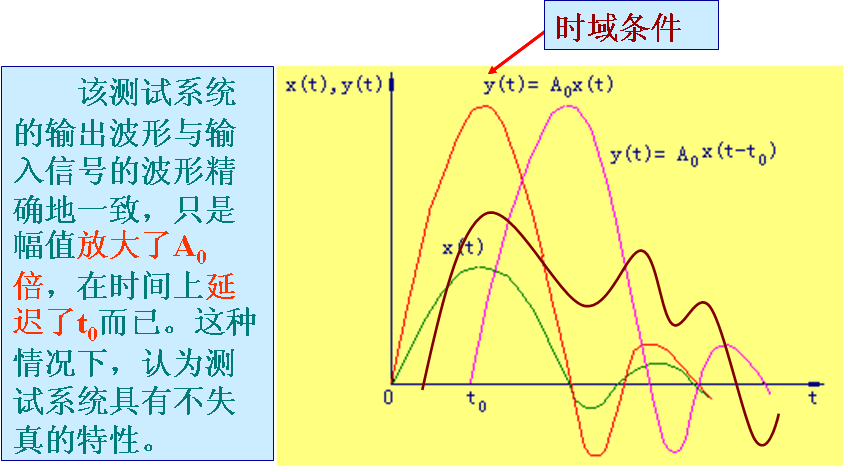
          y(t)=A0x(t- t0) 

      （详细推导如下） 

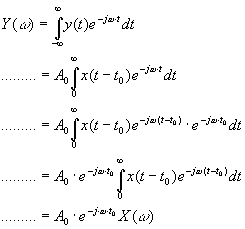
则其幅频和相频特性应分别满足：

         A(ω)=A0=const；φ(ω)=-t0ω

即为实现不失真测试的条件。

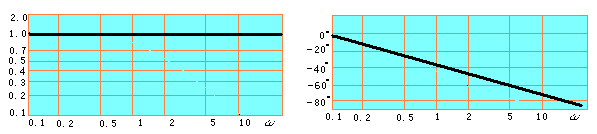
                  不失真测试系统的幅相频特性曲线

1)如果A(ω)不等于常数，引起的失真称为幅值失真；

2)φ(ω)与ω不成线性关系引起的失真称为相位失真。

3)当φ(ω)=0时，输出和输入没有滞后，此时，测试作图才是最理想的。

物理意义: 

1)系统对输入信号中所含各频率成分的幅值进行常数倍数放缩，也就是说，幅频特性曲线是一与横轴平行的直线。

2)输入信号中各频率成分的相角在通过该系统时作与频率成正比的滞后移动，也就是说，相频特性曲线是一通过原点并且有负斜率的直线。

思考题：

某一测试装置的幅频、相频特性如图所示，问哪个信号输入，测试输出不失真？ 

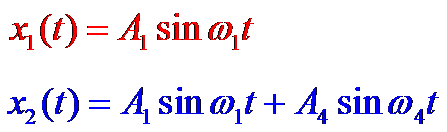
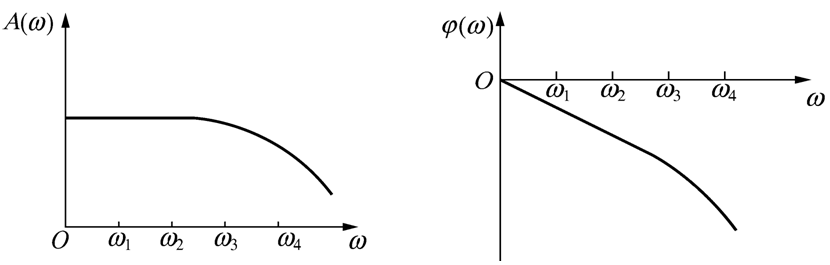
实际测量装置不可能在非常宽广的频率范围内都满足上式的要求，所以通常测量装置既会产生幅值失真，也会产生相位失真。下图表示四个不同频率的信号通过一个具有图中A(ω)和φ(ω)特性的装置后的输出信号。四个输人信号都是正弦信号（包括直流信号），在某参考时刻t＝0，初始相角均为零。图中形象地显示各输出信号相对输入信号有不同的幅值增益和相角滞后。

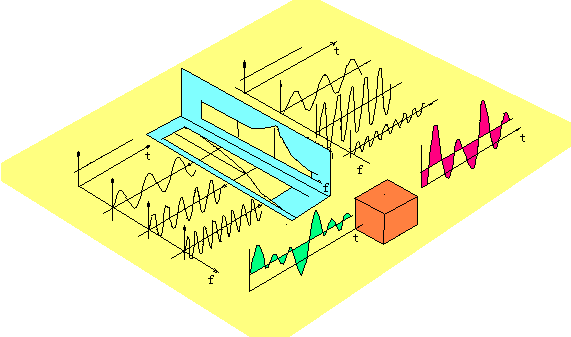
                            信号中不同频率成分通过测量装置后的输出

从实现不失真测试的条件和其他工作性能综合来看，对于一阶系统而言，时间常数越小，则时域中系统的响应速度越快，频域中近于满足不失真测试条件的频带也越宽，因此一阶系统的时间常数τ原则上越小越好。

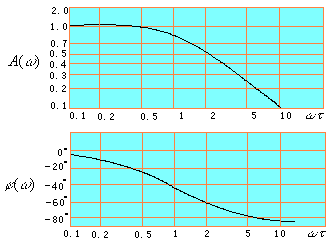
一阶系统的频率特性

对于二阶系统，当ξ＝0.7左右，在特性曲线中范围内，的数值较小，相频特性曲线接近直线，A（ω）在该频率范围内的变化不超过5％，因此该频率范围内波形失真较小。此时系统可获得最佳的综合特性，这也是设计或选择二阶测试系统的依据。

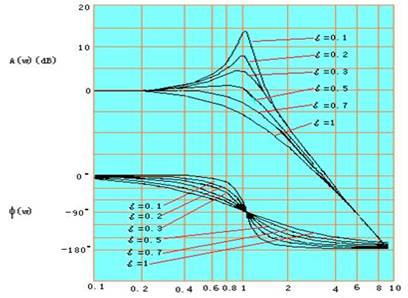
                               二阶系统的频率特性

测量系统中，任何一个环节产生的波形失真，必然会引起整个系统最终输出波形失真。虽然各环节失真对最后波形的失真影响程度不一样，但是原则上在信号频带内都应使每个环节基本上满足不失真测量的要求。

一、时域不失真条件

二、频域不失真条件：

要使信号通过测试装置后不产生波形失真，测试装置的幅频和相频特性应分别满足