1.4 几种典型信号的频谱（1学时）

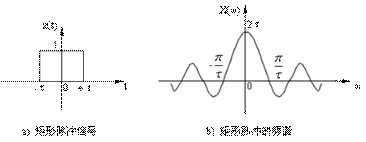
矩形脉冲信号的频谱如图2.3.3所示，由此可以得出以下结论： 
    1. 当脉冲宽度τ很大时，信号的能量将大部分集中在ω＝0附近（图1.3.4(a)）；
    2. 当脉冲宽度τ→∞时，脉冲信号变成直流信号，频谱函数只在ω＝0处存在（图2.3.4(b)）；

3. 当脉冲宽度τ减小时，频谱中的高频成分增加，信号频带宽度增大（图2.3.4(c)）；

        4. 当脉冲宽度τ→0时，矩形脉冲变成无穷窄的脉冲（相当于单位冲击信号），频谱函数成为一条平行于ω轴的直线，并扩展到全部频谱范围，信号的频带宽度趋于无穷大（图2.3.4(d)）

                                                

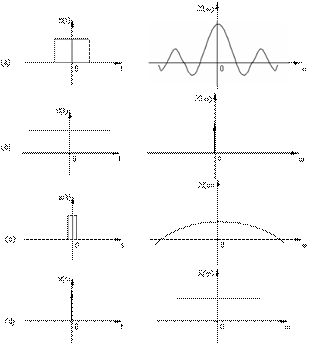
                                                                                  图1.3.4

一、单位脉冲函数(δ函数) 的频谱

1. δ函数定义

在ε时间内矩形脉冲(或三角形脉冲及其它形状脉冲)，其面积为1,当ε0 时， 的极限，称为δ函数，如图所示。δ函数用标有1的箭头表示。

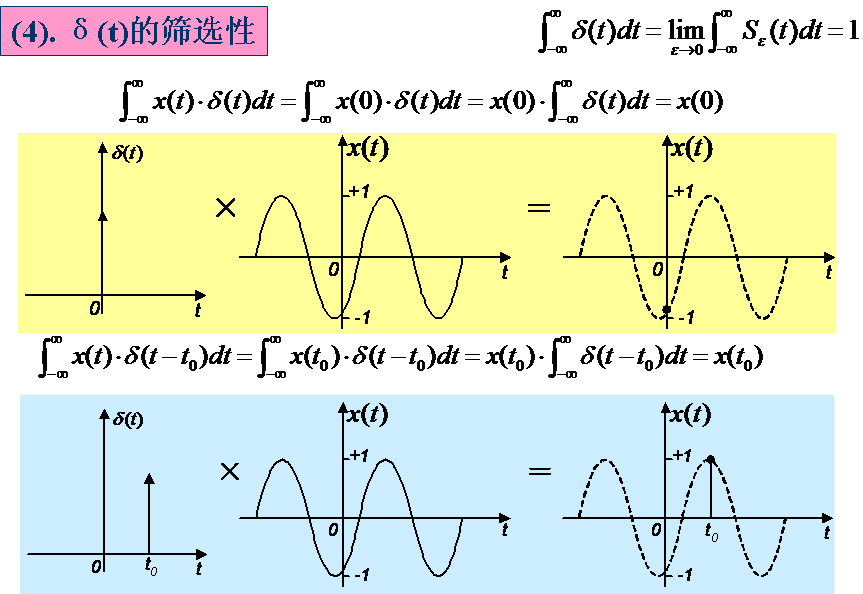
显然δ(t)的函数值和面积(通常表示能量或强度)分别为

                        (1-43)

     (1-44)

某些具有冲击性的物理现象，如电网线路中的短时冲击干扰，数字电路中的采样脉冲，力学中的瞬间作用力，材料的突然断裂以及撞击、爆炸等都是通过δ函数来分析，只是函数面积（能量或强度）不一定为1，而是某一常数K。由于引入δ函数，运用广义函数理论，傅里叶变换就可以推广到并不满足绝对可积条件的功率有限信号范畴。

2. δ函数的频谱

_{δ函数的频谱将δ函数进行傅里叶变换，即可得到其频谱函数：}

                                  (1-46)        由此可见，时域的脉冲信号具有无限宽广的频谱，而且各频率上的信号强度都相等。在信号的检测中，一般爆发电火花地方(如雷电、火花塞等)都会对测试系统引起严重干扰，这是因为尖脉冲(类似δ函数，能量均匀地分布在0~∞的频带内)的高频部分以射频形式发射出来，对测试系统形成干扰的缘故。凡是频谱为常数的信号俗称白噪声。  “白”是由白色光引申而来，意即白色的光谱频率丰富。δ脉冲就是一种理想的白噪声。

可见δ函数具有等强度、无限宽广的频谱，这种频谱常称为“均匀谱”。

利用对称、时移、频移性质，还可以得到以下傅里叶变换对。

3.δ函数的性质

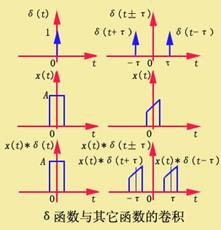
                   卷积性

工程上经常遇到的是频谱卷积运算

可见函数X(f)和δ函数卷积的结果，就是X(f)图形搬迁(以发生δ函数的位置作为新坐标原点的重新构图)，如图所示。

㈢正、余弦函数的频谱密度函数

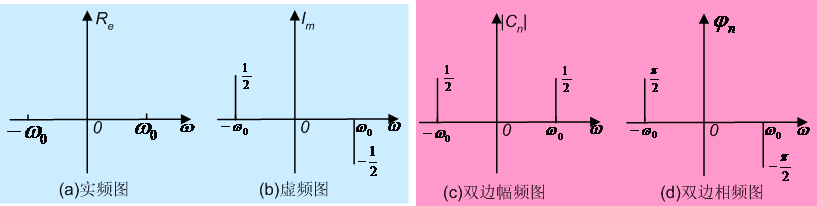
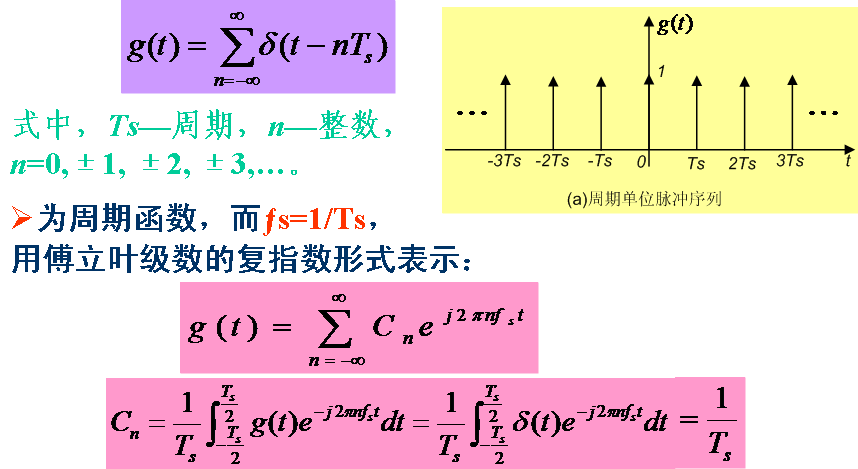
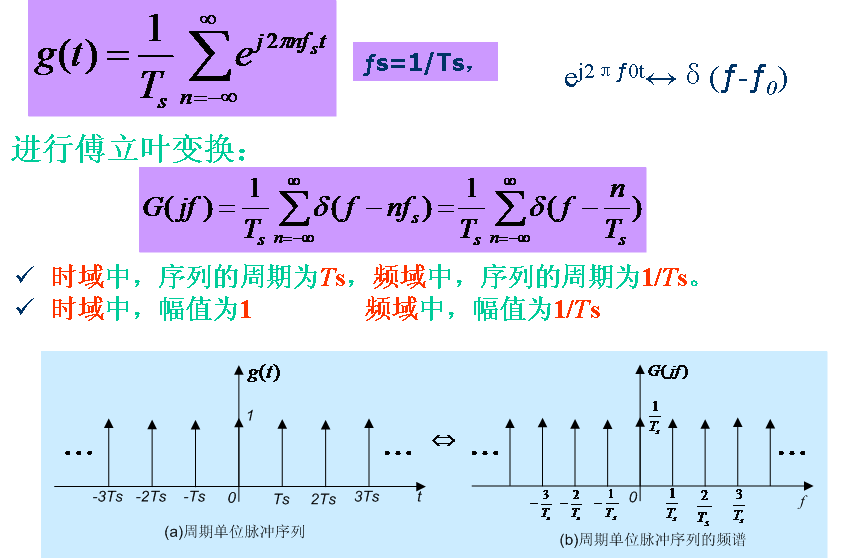
（四）周期单位脉冲序列的频谱

5 频谱分析的应用

频谱分析主要用于识别信号中的周期分量，是信号分析中最常用的一种手段。

小    结

根据信号的不同特征，信号有不同的分类方法。采用信号“域”的描述方法可以突出信号不同的特征。信号的时域描述以时间为独立变量，其强调信号的幅值随时间变化的特征；信号的频域描述以角频率或频率为独立变量，其强调信号的幅值和相位随频率变化的特征。

一般周期信号可以利用傅里叶级数进行展开，包括三角函数和复指数展开。利用周期信号的傅里叶级数展开可以获得其离散频谱。常见周期信号的频谱具有离散性、谐波性和收敛性。

把非周期信号看出周期趋于无穷大的周期信号，有助于理解非周期信号的频谱。利用傅里叶变换可以获得非周期信号的连续频谱，理解并掌握频谱密度函数的含义、傅里叶变换的主要性质和典型信号的频谱并能灵活运用具有重要意义。

对于周期信号，同样可以利用傅里叶变换获得其离散频谱，该频谱和利用傅里叶级数的复指数展开的方法获得的频谱是一样的。

思考题

1-1举例说明你学习和生活中的周期信号、非周期信号、连续信号、离散信号、瞬态信号、功率信号和能量信号？

1-2 试指出下列信号哪些为能量信号？哪些为功率信号？或者两者都不是。

⑴；

⑵；

⑶；

⑷；

⑸；

⑹。

1-3 通过收集资料举例说明信号可以从哪些域的角度进行分析以获取需要的信息？

1-4 通过收集资料，阐述数字信号是如何获得的？

1-5 用你自己的语言叙述，为什么瞬态信号的频谱是连续频谱？

1-6 从傅立叶级数和傅立叶变换的角度，分析一般周期信号的频谱？

1-7 总结周期单位脉冲序列及其频谱的特点。

1-8 从信号卷积的角度，分析复杂周期信号（如方波信号）被矩形窗函数阶段后的信号的频谱？

 
本章课件