2.6 测试系统动态特性的测定

任何一个测试系统，都需要通过实验的方法来确定系统输入、输出关系，这个过程称为标定。即使经过标定的测试系统，也应当定期校准，这实际上就是要测定系统的特性参数。

目的：在作动态参数检测时，要确定系统的不失真工作频段是否符合要求。

方法：用标准信号输入，测出其输出信号，从而求得需要的特性。

F标准信号:正弦信号、脉冲信号和阶跃信号。

1．频率响应法

  理论依据：                     

方法：以频率为ω的正弦信号 x(t)=A₀sinωt  作用于装置，在输出达到稳态后测量输出和输入的幅值比和相位差，则幅值比就是该ω对应的幅频特性值，相位差与该ω对应的即为相频特性值。

从接近零频率的足够低的频率开始，以增量方式逐点增加ω到较高频率，直到输出量减小到初始输出幅值的一半为止，即可得到A(ω)- ω；φ(ω)- ω特性曲线。 

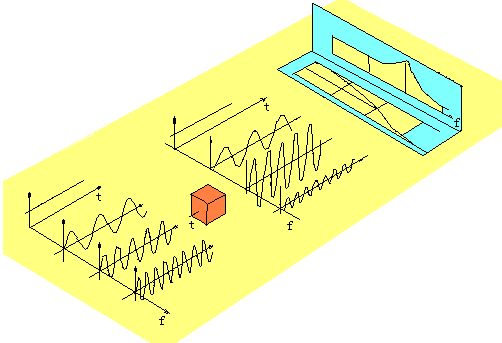
                             频率响应法测量系统特性

一阶系统的幅频、相频特性

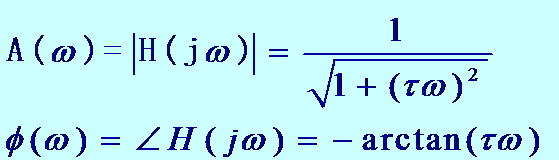
由一阶系统的幅频特性公式可知：

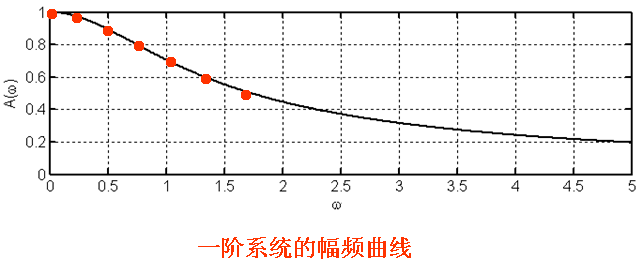
对于一阶测试系统，主要特性参数是时间常数t，可以通过幅频、相频特性数据直接计算t值

Ø对于二阶系统，通常通过幅频特性曲线估计其固有频率wn和阻尼比x。

1）在φ(ω) – ω相频特性曲线上，当ω=ωn时，φ(ωn)=-90º，由此可求出固有频率ωn。

2）φ’(ω)=-1/ξ，所以，作出曲线φ(ω) – ω在ω=ωn处的切线，即可求出阻尼比ξ。

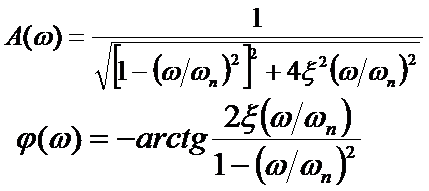
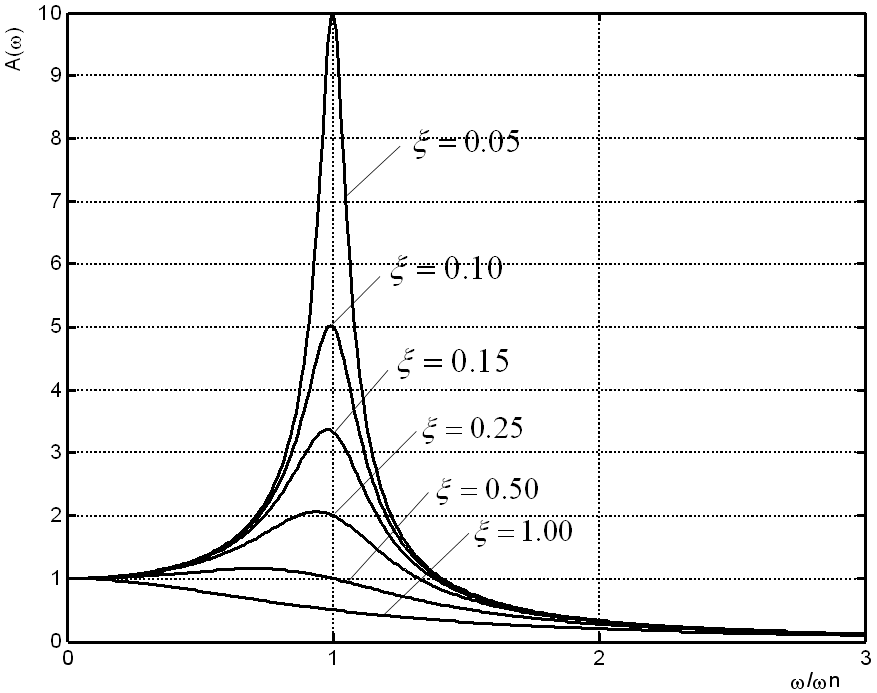
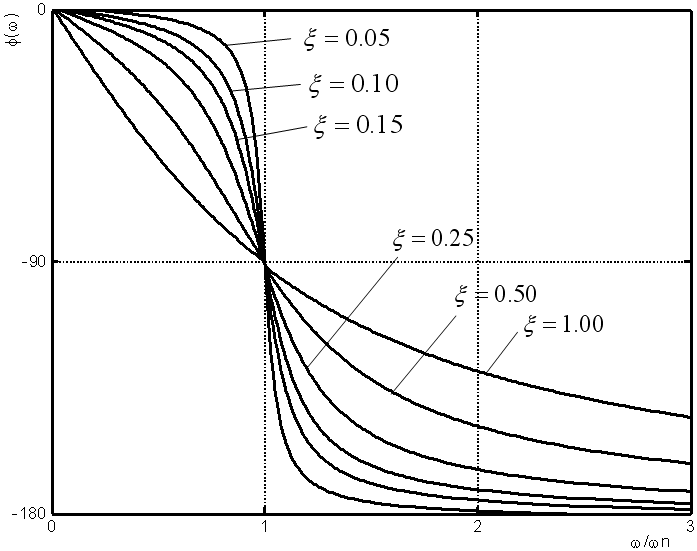
较为精确的求解方法   欠阻尼系统（x<1)

对于ξ＜1的欠阻尼二阶系统，其幅频特性曲线的峰值在ωr处。

  1）求出A(ω)的最大值及其对应的频率ωr；

Ø由于这种方法中A(ωr)和ωr的测量可以达到一定的精度，所以由此求解出的固有频率ωn和阻尼比ξ具有较高的精度。

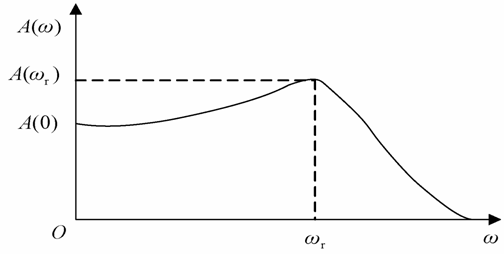
阻尼系数也可以由峰值点附近的两个半功率点的频率计算。

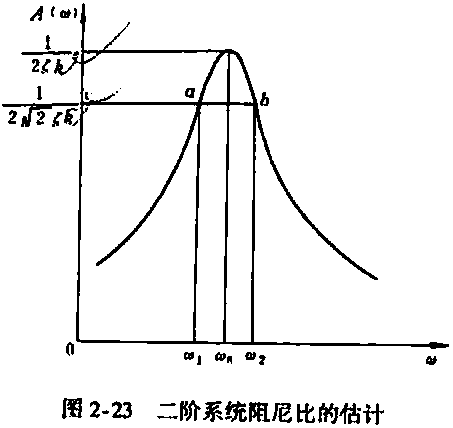
2. 阶跃响应法

一阶系统：

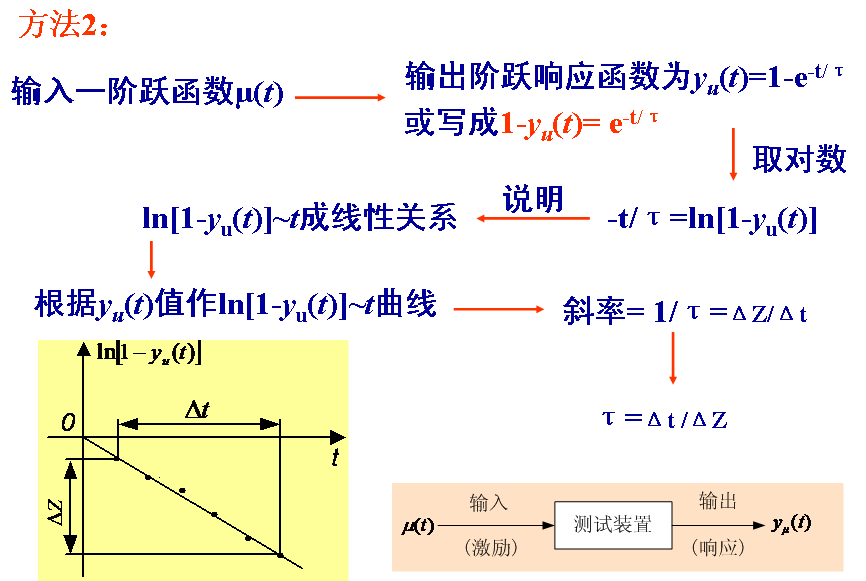
方法1：

ü时间常数τ是唯一表征系统动态特性的参数。

ü当输入响应达到稳态值的63.2%时，所需要的时间就是一阶系统的时间常数。

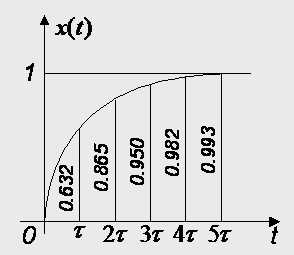
缺点：

ü很难做到精确的测试；

ü求取时间常数τ未涉及响应全过程，是个别瞬时值，这样测量结果的可靠性差。 

二阶系统

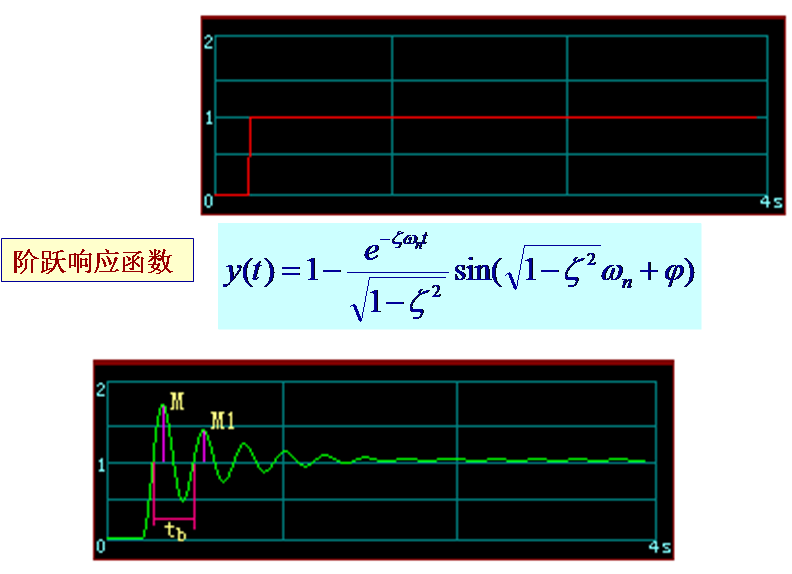
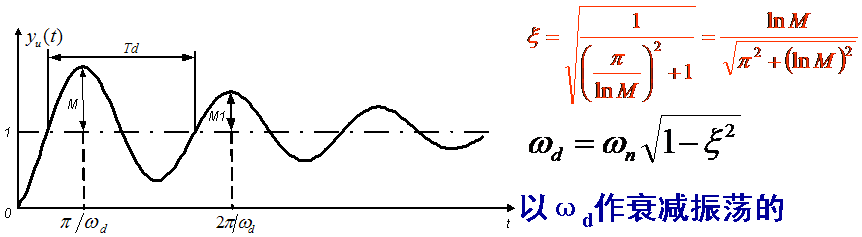
例 2.3:对一个典型二阶系统输入一脉冲信号，从响应的记录曲线上测得其振荡周期为4ms，第三个和 第十一个振荡的单峰幅值分别为12mm和4mm。试求该系统的固有频率 ωn 和 阻尼率ζ。

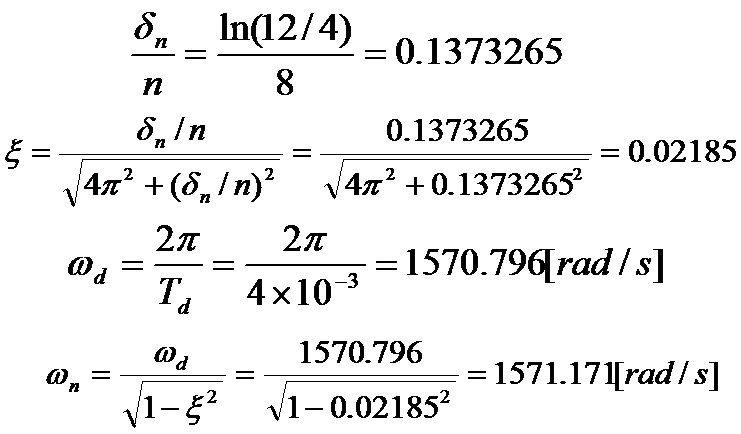
                                                               典型二阶系统应用