5.1 随机信号

概述

  随机信号具有不可被预测的特性（其幅值、相位  变化不可预知），不能用数学关系式描述，只能由自身的统计特性和频谱特性加以表征。

  研究随机信号具有现实意义：

  确定性信号仅仅是在一定条件下出现的特例，或者忽略随机因素影响抽象的模型。

  信号总是受到各种随机干扰的影响，如何排除随机干扰来辨识和测量信号？

 对随机信号按时间历程所作的各次长时间观测记录称为样本函数，记作xi(t)在同样的条件下，不同时间段的各样本函数的集合 称为总体，记作：         {x(t)}=x1(t),x2(t),..,xi(t)}  {x(t)}就表示一个随机过程。只有足够的样本函数，可得到其概率意义上的统计规律。

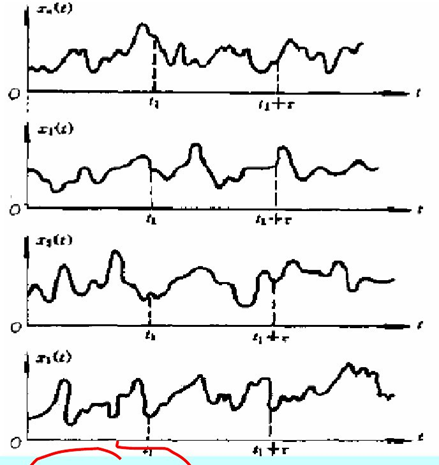
各态历经性（遍历性）：在平稳随机过程中，若任一单个样本函数的时间平均统计特征等于该过程的集合平均统计特征。

  工程上遇到的大都可以近似地当作各态历经随机过程来处理，以有限长度样本记录的分析来判断、估计被测对象的整个随机过程。

要完整地描述一个各态历经随机过程，理论上要有无限长时间记录，但实际上这是不可能的。通常用统计方法对以下三个方面进行数学描述：

  1）幅值域描述:  均值、均方值、方差、概率密度函数等。

  2）时域描述:  自相关函数、互相关函数。

  3）频域描述:  自功率谱密度函数、互功率谱密度函数

信号的幅值域分析

 均值
  

式中，T为样本长度，观测时间

均值：反映了信号变化的中心趋势，也称之为直流分量。

方差

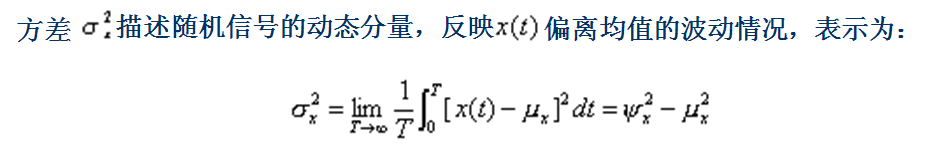
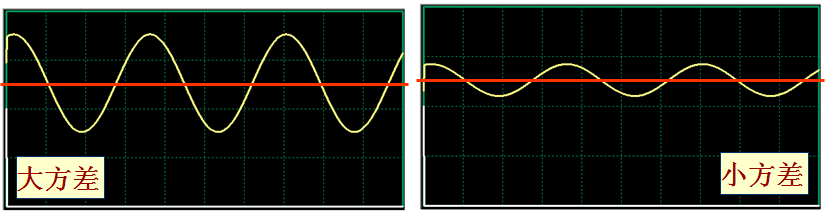
   方差：反映了信号绕均值的波动程度。 

均方值

  其正平方根值，又称为有效值(RMS)，也是信号平均能量的一种表达。

信号的幅值域分析

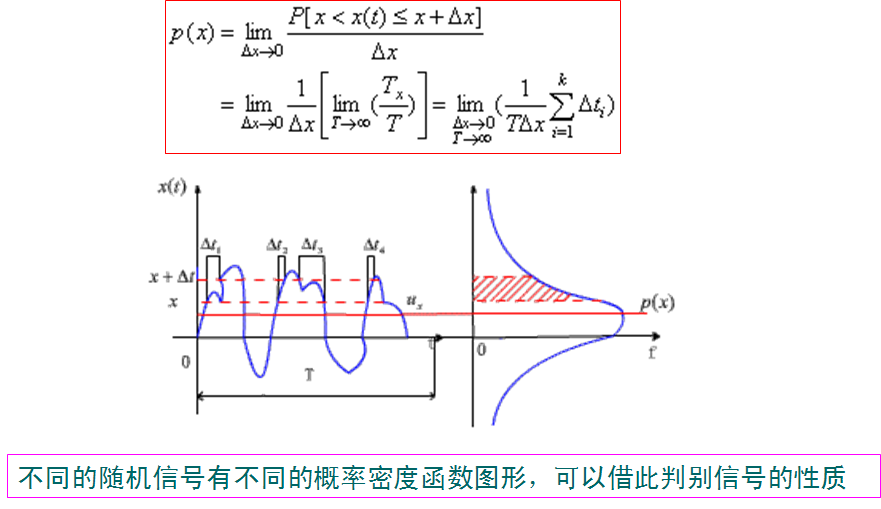
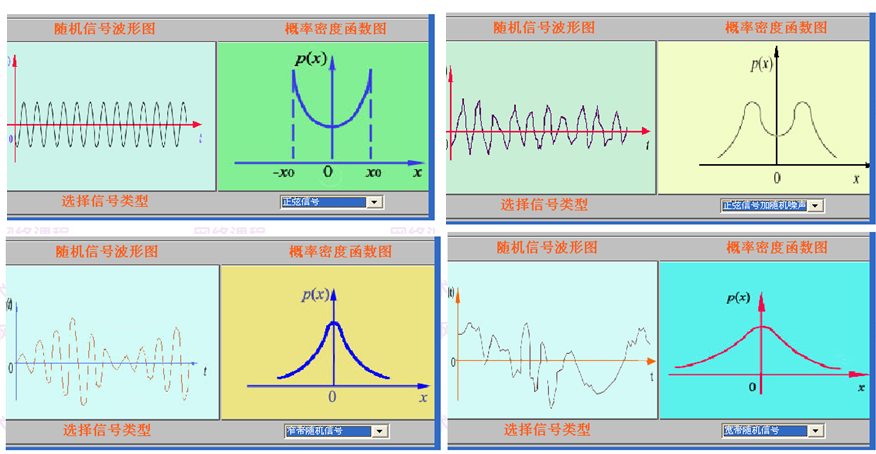
二 概率密度函数

 以幅值大小为横坐标，以每个幅值间隔内出现的概率为纵坐标进行统计分析的方法。它反映了信号落在不同幅值强度区域内的概率情况。

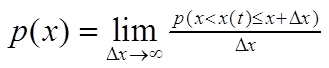
概率密度函数公式表达：