常见题型精解
例2.1 试画出图示两种机构的运动简图,并说明它们为何种机构。在图2.8a中偏心盘1绕固定轴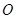 转动,迫使滑块2在圆盘3的槽中来回滑动,圆盘3相对于机架4转动;在图2.8b中偏心盘1绕固定轴
转动,迫使滑块2在圆盘3的槽中来回滑动,圆盘3相对于机架4转动;在图2.8b中偏心盘1绕固定轴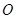 转动,通过构件2,使滑块3相对于机架4往复移动。
转动,通过构件2,使滑块3相对于机架4往复移动。
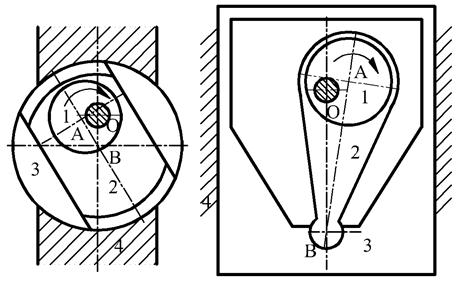
图2.8a 图2.8b
答案:
图a的机构运动简图有两种画法,见图2.9。其中(1)是导杆机构,(2)是曲柄摇块机构。
图b的机构运动简图画法见图2.9的(3),是曲柄滑块机构。
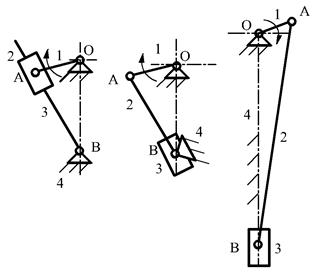
(1) (2) (3)
图2.9
【评注】
这道题主要考查对各种形式四杆机构及其演化机构的判别能力,因此要特别熟悉各种类型的机构。此外正确绘制机构运动简图是解本道题的前提,要能从实际图例中抓住本质,分析清楚两构件间的运动副类型,从而正确地将机构运动简图绘制出来。
例2.2 如图2.10所示铰链四杆机构中,已知各杆长度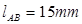 ,
,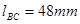 ,
,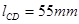 ,
,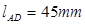 。
。
(1)判断该机构为何种机构;
(2)已知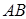 为原动件,用作图法确定从动件
为原动件,用作图法确定从动件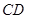 的最大摆角
的最大摆角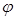 ,机构的极位夹角
,机构的极位夹角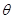 ,并求行程速度变化系数
,并求行程速度变化系数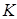 。
。
(3)当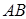 为原动件时,用作图法求机构的最小传动角
为原动件时,用作图法求机构的最小传动角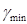 。
。
(4)问此机构什么时候会有死点存在。
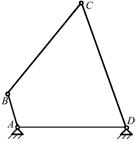
图2.10
答案:
(1)由已知条件知最短杆是连架杆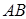 ,最长杆是另一连架杆
,最长杆是另一连架杆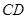 。
。
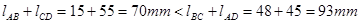 ,
,
因此周转副是存在的。同时最短杆的邻边是机架,因此这是曲柄摇杆机构。
(2)当摇杆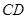 处于两个极限位置时,曲柄
处于两个极限位置时,曲柄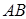 和连杆
和连杆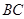 处于两次共线位置。取适当的比例尺作出这两极限位置时的机构位置简图
处于两次共线位置。取适当的比例尺作出这两极限位置时的机构位置简图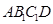 和
和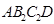 ,
,
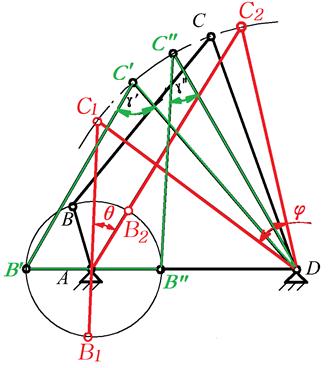
这时摇杆两次位置之间的夹角就是其最大摆角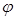 ,由图量得
,由图量得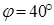 ;两次共线位置之间的锐角就是极位夹角
;两次共线位置之间的锐角就是极位夹角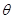 ,由图量得
,由图量得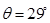 。因此可求得:
。因此可求得:
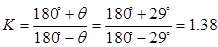
(3)最小传动角出现的位置是曲柄与机架的两次共线位置之一。用作图法作出两次共线位置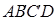 和
和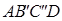 ,由图中量得
,由图中量得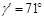 ,
,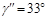 ,因此
,因此 。
。
(4)当以曲柄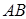 为原动件时,连杆
为原动件时,连杆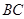 与摇杆
与摇杆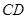 不可能共线,因此机构没有死点位置。但若以摇杆
不可能共线,因此机构没有死点位置。但若以摇杆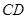 为原动件,则此时从动件曲柄
为原动件,则此时从动件曲柄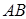 与连杆
与连杆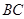 会有两次共线位置,传动角为零,因此机构存在死点位置。
会有两次共线位置,传动角为零,因此机构存在死点位置。
【评注】
这道题主要考查根据杆长判断四杆机构为何种机构,并考查四杆机构主要特性方面的知识。
(1)根据杆长条件判断是否存在整转副,若有再判断什么杆件是机架最终确定机构类型;如果不满足杆长条件,则不论以谁为机架都是双摇杆机构。
(2)摇杆的两次极限位置对应曲柄与连杆两次共线位置,这样同时就可以把摇杆的摆角和机构的极位夹角确定下来,然后根据公式就可以求解形成速度变化系数。
(3)对于机构最小传动角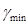 出现的位置要很清楚,是在曲柄与机架两次共线位置之一,这样就很容易作图求解了。
出现的位置要很清楚,是在曲柄与机架两次共线位置之一,这样就很容易作图求解了。
(4)对于死点就是机构传动角为零的时候,因此可以通过判断机构是否有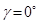 的位置,从而判断机构是否有死点。通常对铰链四杆机构来说,传动角的大小等于连杆和从动件之间的夹角,因此只要二者有共线的情况就会出现死点位置,否则没有。
的位置,从而判断机构是否有死点。通常对铰链四杆机构来说,传动角的大小等于连杆和从动件之间的夹角,因此只要二者有共线的情况就会出现死点位置,否则没有。
例2.3已知曲柄摇杆机构的摇杆长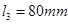 ,机架长
,机架长 ,且曲柄中心在摇杆中心水平线之上,摆角
,且曲柄中心在摇杆中心水平线之上,摆角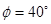 ,行程速度变化系数
,行程速度变化系数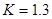 ,求曲柄和连杆长度。
,求曲柄和连杆长度。
答案:
作图步骤如下(见图2.11):
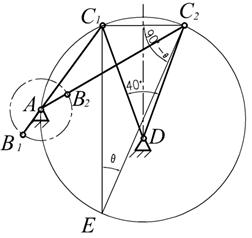
图2.11
(1)求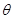 ,
,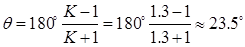 ;并确定比例尺
;并确定比例尺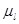 。
。
(2)作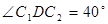 ,
, 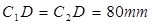 。
。
(3)以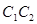 为底作
为底作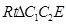 ,
,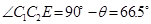 ,
,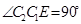 。
。
(4)作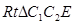 的外接圆,在圆上取点
的外接圆,在圆上取点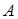 ,使
,使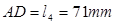 ,
,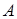 点位置在
点位置在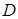 点之上。
点之上。
(5)量得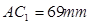 ,
,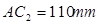 。
。
解得:
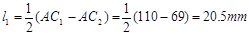 ,
,
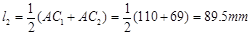 。
。
【评注】
此题属于已知行程速比系数设计四杆机构问题。因此首先按照一般步骤把固定铰链中心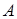 所在的圆找到,然后机架长度把具体位置确定下来。实际
所在的圆找到,然后机架长度把具体位置确定下来。实际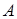 点位置在
点位置在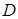 点之上的有两个,但机构的尺寸结果是一样的。
点之上的有两个,但机构的尺寸结果是一样的。
例2.4图2.12为偏置的曲柄滑块机构。已知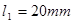 ,
,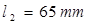 ,
,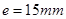 ,用图解法求:(1)曲柄主动时滑块的行程
,用图解法求:(1)曲柄主动时滑块的行程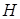 、极位夹角
、极位夹角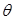 、行程速度变化系数
、行程速度变化系数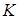 和机构的最大压力角
和机构的最大压力角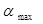 ;(2)滑块主动时机构的死点位置。
;(2)滑块主动时机构的死点位置。
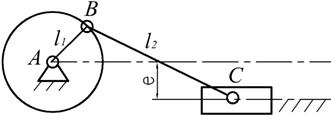
图2.12
答案:
(1)用图解法求,见图2.13。要求滑块的行程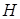 ,就要找到滑块的两个极限位置
,就要找到滑块的两个极限位置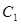 、
、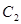 。这两点的特点是,曲柄
。这两点的特点是,曲柄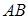 与连杆
与连杆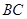 在滑块达到极限位置时成直线。则:
在滑块达到极限位置时成直线。则:
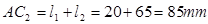 ,
,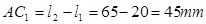
选择比例尺,以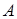 点为中心,以
点为中心,以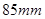 为半径画弧,与滑块轨迹线交于
为半径画弧,与滑块轨迹线交于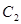 点;以
点;以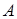 点为中心,以
点为中心,以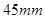 为半径画弧,与滑块轨迹线交于
为半径画弧,与滑块轨迹线交于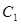 点。
点。
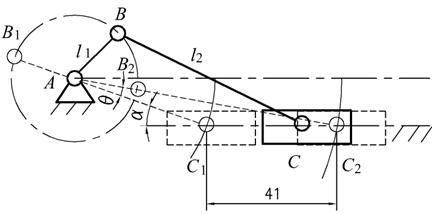
图2.13
由图上直接量得:滑块行程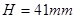 ;极位夹角
;极位夹角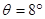 。滑块在
。滑块在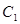 点时压力角最大
点时压力角最大 。
。
行程速比系数: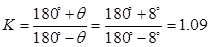
(2)滑块主动时,图中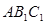 、
、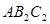 就是死点位置,因为此时
就是死点位置,因为此时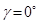 。
。
【评注】
本题还是主要考查极限位置时构件的几何关系,抓住这一点本题就迎刃而解。曲柄摇杆机构的压力角经分析是连杆和滑块轨迹线之间的夹角,从图上分析,只有在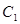 点时这个角度可以取得最大值。对于死点位置,还是要牢记此时
点时这个角度可以取得最大值。对于死点位置,还是要牢记此时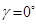 。
。


