地球形状与空间模型
一、地球形状
地球在宇宙中是不停地运动着的(如图2.13所示)。长期以来,人们对地球形状的认识常描述为球体、或椭球体、或不规则的椭球体、或具有高低起伏的扁球体。究竟如何表达地球形状,与人们所要求的精度相关。
图2.13
自然地面实际呈高低起伏状,最高处为珠穆朗玛峰顶,海拔8844.43m,最低马里亚纳海沟底,海拔 -11034m,但两者相差不到20km,若与地球的赤道半径6378.140km和极半径6356.755km相比,或与地球的平均半径6378.14km对比,悬殊较大。若用相同的比例尺缩小来反映地球,则难以表达地表的20km的差别。我们把地球视为“圆球体”,如地球仪,所以在研究地球形状时,主要视精度的需求而定。人们或用规则的椭球体来模拟地球,或用规则的球体来模拟地球,或用大地水准面来模拟真实的地面(如图2.14所示)。换一句话说,对现实世界的数据表达可以采用地球空间模型,地图和GIS其实都是模型,地图以图形符号来记载和表示地理数据;GIS以数字形式来记载和表示地理数据。
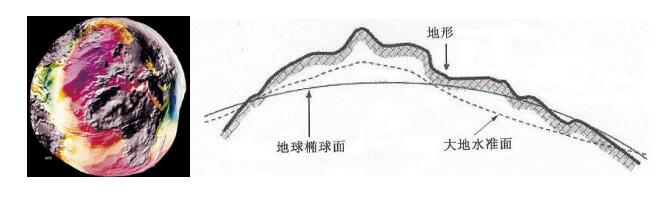
图2.14地球表面
2.2.2 地球空间模型
如何描述地球的形状,这是地图和GIS要解决的重要问题之一。一般可用地球空间模型表达,根据大地测量学的研究成果,常见的地球空间模型有以下几种。
(1)地球的自然表面:是一个高低起伏、不规则的表面,包括海陆表面。
(2)地球大地水准面:假设当海水处于完全静止的平衡状态时,从海平面延伸到所有大陆下部,而与地球重力方向处处正交的一个连续、闭合的水准面,也就是地球引力场的等势面,称为大地水准面。如图2.14所示。
(3)地球椭球体面:以大地水准面为基准建立起来的地球椭球体模型(见图2.15),表面是个规则的数学表面,椭球体的大小通常用两个半径――长半径a(也叫赤道半径)和短半径b(也叫极半径),或由一个半径和扁率u或偏心率e来决定。其中:
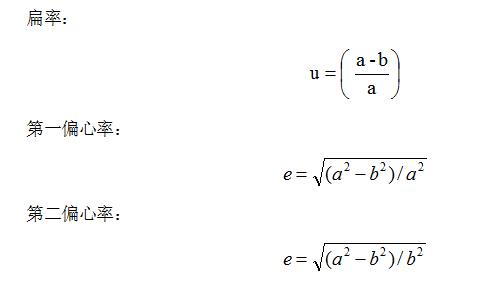
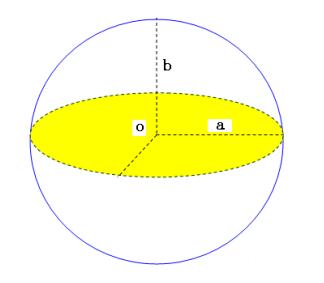
图2.15
对于旋转椭球体的描述,由于计算年代不同,所用方法不同;测定地区不同,其描述方法也不同。一百多年来,各国研究者对地球椭球体进行了众多研究,提出了多组地球椭球体参数。常用参数数据如表2.3。不同的GIS软件,所提供的旋转椭球体模型种类有不同,如Arc/Info软件中提供了30多种旋转椭球体模型。
表2.3 常用的地球椭球体数据
| 椭球体名称 | 提出年代 | 长轴半径a/m | 短轴半径b/m | 扁率u |
| Everest | 1830 | 6 377 276 | 6 356 075 | 1:300.8 |
| Bassel | 1841 | 6 377 379 | 6 356 079 | 1:299.15 |
| Clarke | 1880 | 6 378 249 | 6 356 515 | 1:293.5 |
| Clarke | 1886 | 6 378 206 | 6 356 584 | 1:295.0 |
| Hayford | 1910 | 6 378 388 | 6 356 912 | 1:297.0 |
| Krasovski | 1940 | 6 378 245 | 6 356 863 | 1:298.3 |
| IUGG | 1976 | 6 378 160 | 6 356 775 | 1:298.25 |
| WGS84 | 1984 | 6 378 137.0 | 6 356 752.3 | 1:298.26 |
我国于1954年开始采用前苏联克拉索夫斯基(Krasovski)椭球体作为地球表面几何模型,即1954年北京坐标系。20世纪70年代末建立了新的1980西安坐标系,采用了国际大地测量与地球物理联合会(IUGG)提供的椭球体。1984年后采用了世界大地坐标(WGS84)椭球体,建立的是国家大地坐标系。但由于国家大地坐标系是二维、非地心的坐标系,不仅制约了地理空间信息的精确表达和各种先进的空间技术的广泛应用,无法全面满足当今气象、地震、水利、交通、航空航天等部门对高精度测绘地理信息服务的要求,而且也不利于与国际航线以及与海图的有效衔接,因此,2008年7月1日后启用2000国家大地坐标系,它是全球地心坐标系在我国使用的具体体现,同时,国家测绘局公告2000国家大地坐标系与现行国家大地坐标系转换、衔接的过渡期为8至10年。2000国家大地坐标系采用的地球椭球参数如下:
长半轴 a=6378 137m
扁率f=1/298.257222101
地心引力常数GM=3.986 004418×1 014m3s-2
自转角速度ω=7.292 115×10-5rad• s-1
应用GIS技术来模拟、反演区域地理过程或现象是地学应用的重要发展趋势,但地表不同区域参数的选择(是曲面还是平面,是球体还是椭球体,还是不规则椭球体)是GIS地学应用模型构建的关键(将在第6章介绍)。
(4)数学模型:为解决其他一些大地测量学问题提出的。如类地形面、准大地水准面等。

