3.1 GIS数据结构(1)
要将实际地理世界的实体、现象在GIS概念世界表达,需要建立一定的数据模型来描述地理实体及实体关系。在GIS领域,目前普遍采用了两种数据模型:即基于目标的和基于场的。前者所描述单位与实体世界的目标实体相对应,强调实体的“整体性”,但在实体间的空间关系表达上缺乏便捷的策略,模型通常需要通过复杂的矢量运算;后者描述的对象遍布整个研究空间,模型描述的单位划分为极小的面元,强调实体的“相关性”、“连续性”,但实体的整体性描述不如前者,实体间的关系通过诸如栅格的扩展等“相关性运算”来获取,
数据结构是对数据模型具体的存储实现,通过特定的逻辑组织将地理实体、地理现象在GIS系统中记录下来。与基于场的观点对应的数据结构通常为包括规则格网的栅格结构和不规则格网结构,与基于目标的观点对应的数据结构通常为矢量结构。两者各有优缺点,比较见表3.1。如图3.1所示为同一地区采用不同的数据结构表达的示意图。若不严格区分时,在实际操作中空间数据结构与空间数据模型通常可混用。
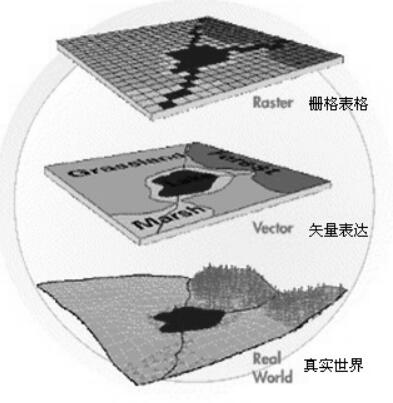
图3.1 同一地区采用不同的数据结构表达的示意图
基于计算机存储角度,数据结构是数据的组织形式,是指在计算机存储、管理和处理的数据逻辑结构。空间数据是一种较复杂的数据类型,涉及到空间特征、属性特征及它们之间关系的描述,非空间数据主要涉及属性数据。从研究数据的历史悠久程度来看,有传统数据结构(主要是关系、层次和网状数据结构)和现代数据结构(语义数据结构、面向对象数据结构)。人们在应用时,具体选择哪种数据结构,主要视GIS应用的目的来定。本章重点介绍:矢量数据结构、栅格数据结构和面向对象的数据结构。
表3.1 矢量与栅格数据优缺点比较
| 优 点 | 缺 点 | |
|
矢量
| l 便于面向现象(土壤类,土地利用单元等) l 结构紧凑,冗余度低,便于描述线或边界 l 利于网络、检索分析,提供有效的拓扑编码,对需要拓扑信息的操作更有效 l 图形显示质量好,精度高 l 位置明显,属性隐含 | l 数据结构复杂,各自定义,不便于数据标准化和规范化,数据交换困难 l 多边形叠置分析困难,没有栅格有效,表达空间变化性能力差 l 不能像数字图像那样做增强处理 l 软硬件技术要求高,显示与绘图成本较高 |
|
栅格
| l 结构简单,易于数据交换 l 叠置分析和地理 (能有效表达空间可变性)现象模拟较易 l 利于与遥感数据的匹配应用和分析,便于图像处理 l 输出快速,成本低廉 l 属性明显,位置隐含 | l 现象识别效果不如矢量方法,难以表达拓扑 l 图形数据量大,数据结构不严密不紧凑,需用压缩技术解决该问题 l 投影转换困难 l 图形质量较低,图形输出不美观,线条有锯齿,需用增加栅格数量来克服,但会增加数据文件 |
一、矢量数据结构表示法
矢量数据结构是通过记录坐标的方式尽可能精确地表示点、线和多边形等地理实体,坐标空间设为连续,允许任意位置、长度和面积的精确定义。矢量数据的显著特点是定位明显,属性隐含。它需用矢量结构模型来表达。
(一)矢量数据模型
1.基于对象的矢量数据简单模型
矢量数据模型是以点为基本单位描述地理实体的分布特征,即每一个地理实体都看作是由点组成的,每一个点用一对(x,y)坐标表示。这里的(x,y)坐标可为地理坐标,也可为平面直角坐标。点状实体由一个单独的点表示;线状实体由一系列有序点串或集表示,点的记录顺序称为线的“方向”;面状实体由一系列首末同点的闭合环或有序点集表示。线状和面状实体在显示时分别以直线段将组成它们的点连接成线段链和多边形,如图3.2.
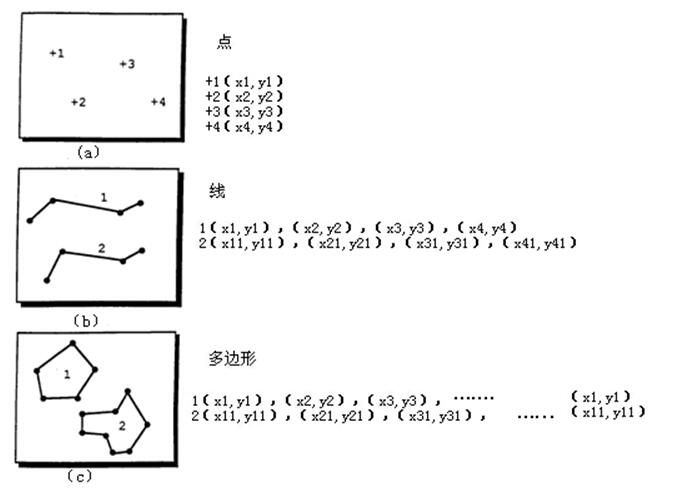
图3.2 基于对象的矢量数据简单模型
2.矢量数据获取方式和编码方法
矢量数据模型只需选取和记录反映地理实体分布形状特征的点,但点的数量对地理实体表示有影响。它非常适合于表示线状实体和面状实体的范围边界。
矢量数据的获取方式(详见第4章)主要有以下三种。
(1)由外业测量获得:可利用测量仪器自动记录测量结果(常称为“电子手薄”),然后转到地理数据库中。
(2)由栅格数据转换获得:利用栅格数据矢量化技术,把栅格数据转换为矢量数据(一般可由转换程序执行)。
(3)由跟踪数字化获得:用跟踪数字化的方法,把地图变成离散的矢量数据。
矢量数据的编码方法主要也有以下三种。
(1)对于点实体和线实体,直接记录空间信息和属性信息。
(2)对于多边形地物,有坐标序列法、树状索引编码法和拓扑结构编码法。
(3)坐标序列法是由多边形边界的x,y坐标对集合及说明信息组成。
三种编码方法评价比较如表3.2所示。
表3.2 矢量数据的编码方法评价
| 方法 | 评价 |
| 第① | 简单,无拓扑 |
| 第② | 树状索引编码法是将所有边界点进行数字化,顺序存储坐标对,由点索引与边界线号相联系,以线索引与各多边形相联系,形成树状索引结构,消除了相邻多边形边界数据冗余问题;拓扑结构编码法是通过建立一个完整的拓扑关系结构,彻底解决邻域和岛状信息处理问题的方法,但增加了算法的复杂性和数据库的大小 |
| 第③ | 最简单的一种多边形矢量编码法,文件结构简单,但多边形边界被存储两次产生数据冗余,而且缺少邻域信息 |
(二)矢量数据结构
常用的矢量数据结构有简单矢量数据结构、拓扑数据结构、不规则三角网数据结构以及网络数据结构等。
1.简单矢量数据结构
在简单矢量数据结构中,空间数据按照基本的空间对象(点、线、面或多边形)为单位进行单独组织。并以地理实体(点、线、面)为单位,将地理实体特征点的坐标存储到一个数据文件中。每个实体由其编号或识别码标识,实体的属性数据(如等级、类型、大小等)设为属性码,以表的形式存储在另一个数据文件中,当需要查询、显示或分析某一实体的属性数据时,GIS以实体编号为关键字从属性数据文件中将它们读取出来。如(x,y)坐标或坐标串表达,其特点是结构简单,存取便捷。数据结构见表3.3和表3.4。
表3.3简单点的矢量数据结构文件
| 标识码 | 属性码 | X、Y坐标 |
| …… | …… | …… |
表3.4简单线的矢量数据结构文件
| 标识码 | 属性码 | X、Y坐标串 |
| …… | …… | …… |
多边形的矢量数据结构与线的类似,但坐标串的首尾坐标相同。构成多边形边界的各个线段,以多边形为单元进行组织。
多边形矢量模型结构如图3.3所示。其中图3.3(a)表达的多边形既不连通也无邻接关系,它是早期的矢量模型之一,有人称它为“面团(Spaghetti)结构”。边界坐标数据和多边形单元实体一一对应,各个多边形边界都单独编码和数字化,正是由于这种特性,表示两个面状实体共同边界的数据需数字化和存储两遍,从而导致数据冗余和表示上的不一致。不过在对同一条曲线重复数字化时,不太可能准确地选择相同点,因此,两个具有共同边界的面状实体在显示时会出现边界的交叉导致出现许多狭小的多边形,这些狭小多边形的存在会给某些GIS应用带来麻烦。此外,这种结构由于没有反映地理实体的拓扑特性,寻找相邻或包含的地理实体、最佳路径分析等都不能有效地执行。图3.3(b)至(c)是后期改进的表达结构。如(b)和(c)的结构具有连通和邻接特性,(d)除了连通和邻接性外,还有方向性和包含性特征。图3.3(b)至(d)的模型结构可称为“面状矢量拓扑数据结构”。
2.拓扑数据结构
拓扑数据结构除了存储地理实体的坐标数据以外,还以计算机可以识别的方式存储反映地理实体拓扑特性,即实体之间的邻接、连接和包含关系。在拓扑数据结构中,点状实体仅以其编号和一对(x,y)坐标表示和存储。线状实体则表示为线段弧,又称为弧段(Arc)。
表示线状实体的拓扑数据结构见图3.4、表3.5和表3.6。
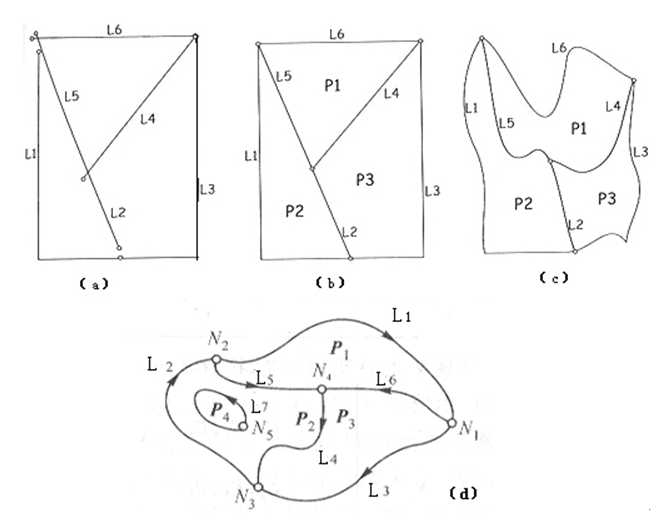
图3.3 面的矢量数据结构
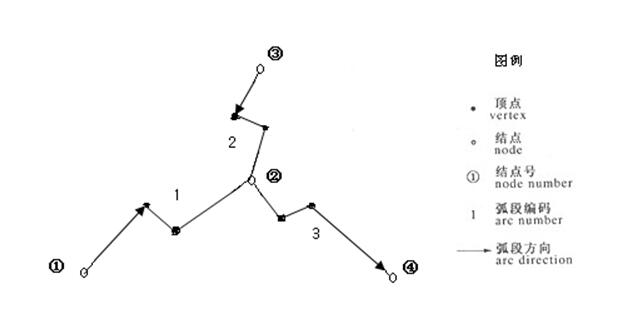
图3.4线状实体多边形
表 3.5弧段——结点表
| 弧段编码 Arc# | 起始点 From_node | 终结点 To_node |
| 1 | 1 | 2 |
| 2 | 3 | 2 |
| 3 | 2 | 4 |
表3.6 弧段——坐标表
| 弧段编码 Arc# | x,y 坐标 (x,y pairs) |
| 1 | (10,17)(22,31)(30,28)(50,50) |
| 2 | (53,90)(45,73)(53,70)(50,50) |
| 3 | (50,50)(60,37)(70,42)(90,15) |
每条弧段都有两个端点,称为结点(Node),弧段上其他点称为顶点(Vertex)、弧段起始点称为起结点(From_node),终点为终结点(To_node),沿弧段从起结点到终结点标识着弧段的方向。拓扑数据结构通常以两个数据文件分别存储组成弧段的结点和所有点的坐标数据(如图3.3所示)。一个数据文件存储每段弧的起结点和终结点,称为“弧段――结点表”,它包含了线状实体连接的拓扑特性方面的信息。第二个数据文件存储组成弧段的所有点的坐标,称为“弧段――坐标表”,用于线状实体的定位如表3.5和3.6所示。
面状实体可看成是由一系列的弧段组成的多边形。图3.5和表3.7、3.8、3.9显示了一个离散型面状实体的拓扑数据结构,表示了四个多边形编号从1到4,整个区域以外的范围编号为0。这个拓扑数据结构以三个数据文件分别存储组成各个多边形的弧段(多边形――弧段表),坐标数据(弧段――坐标表)以及各弧段与相邻多边形之间的关系(左――右多边形表)。
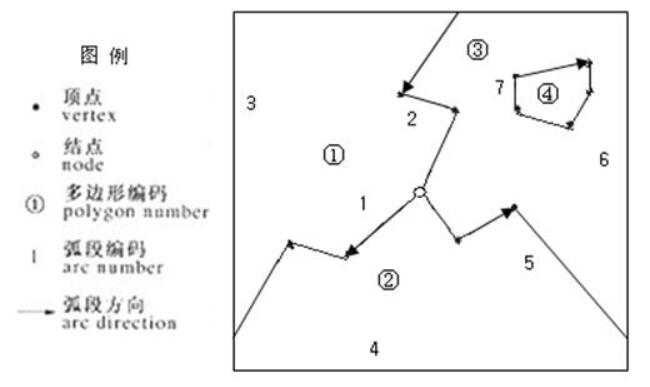
图 3.5面状实体多边形
表3.7 多边形——弧段表 Polygon-arc list
| 多边形编码Polygon# | 弧段编码Arc# |
| 1 | 1,2,3 |
| 2 | 1,4,5 |
| 3 | 2,5,6 |
| 4 | 7 |
表3. 8 左——右多边形表
| 弧段编码 Arc# | 左多边形 Left_poly | 右多边形 Right_poly |
| 1 | 2 | 1 |
| 2 | 3 | 1 |
| 3 | 0 | 1 |
| 4 | 2 | 0 |
| 5 | 2 | 3 |
| 6 | 3 | 0 |
| 7 | 3 | 4 |
表3.9 弧段坐标表
| 弧段编码 Arc# | x,y坐标 x ,y pairs |
| 1 | (50,50)(30,28)(22,31)(10,17) |
| 2 | (53,90)(45,73)(53,70)(50,50) |
| 3 | (10,17)(10,90)(53,90) |
| 4 | (10,17)(10,10)(90,10)(90,15) |
| 5 | (50,50)(60,37)(70,42)(90,15) |
| 6 | (90,15)(90,90)(53,90) |
| 7 | (65,66)(78,66)(77,55)(71,51)(64,54)(65,66) |
拓扑数据结构将每一地理实体的属性数据单独存放在另一个数据文件中,在需要时以地理实体的编号为关键字读取所需数据,这点与简单矢量数据结构一样。属性数据文件可以是一个数据文件记录之间没有结构联系的展开文件,或是以一定数据模型存储的数据库文件。
拓扑数据结构具有表示地理实体的方法简单、数据存储效率高、可检查数据的输入是否有误、可利用最小边界矩形快速运算,以及地图输出质量好等,因此,已被广泛应用于GIS,特别适合表示存储离散型面状的实体数据。但不同的GIS系统所采用的拓扑数据结构不一定相同。这里谈及的是拓扑数据结构主要取自Arc/Info软件,其他GIS软件的拓扑数据结构包括:双重独立编码(简称DIME)、多边形转换器(简称POLYVERT)、 地理编码和参照系统拓扑集成(简称TIGER)等。
3.不规则三角网(TIN)数据结构
不规则三角网(Triangulated IrregularNetwork,简称TIN):是根据一系列不规则分布的数据点产生的,每个数据点由(x,y,z)表示,这里x,y为点的坐标,z为所表示的地理实体在该点的属性值,如高程值、温度值等。TIN将数据点以直线相连形成一个不规则三角网,网中所有三角形相互邻接,互不相交,互不重叠,如图3.6所示。图3.7为不规则三角网在地形表达上的应用示图。
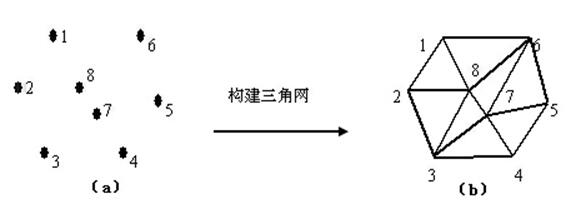
图3.6 不规则三角网和多边形形成

图3.7 不规则三角网在地形表达上的应用图示
将不规则分布数据点连接成三角网的方法有好几种,其中最常用的为狄诺里(Delaunay)三角形。使用Delaunay三角构网法形成的每一个三角形,它的外接圆不含有除三个顶点以外的其他数据点,而这个外接圆的圆心正是与该三角形三个顶点相对应的多边形(也称泰森多边形,Thiessen或Voronoi)的公共顶点,如图3.8所示。泰森多边形可用于GIS定性分析、统计分析、邻近分析等。
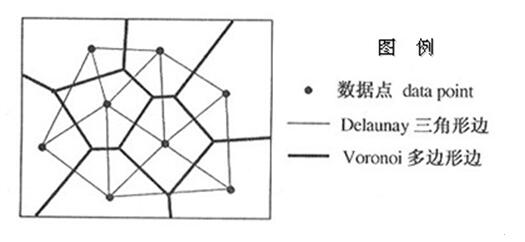
图3.8 Delaunay三角网和Voronoi多边形
泰森多边形具有以下特性。
(1)每个泰森多边形内仅含有一个离散点数据。
(2)泰森多边形内的点到相应离散点的距离最近。
(3)位于泰森多边形边上的点到其两边的离散点的距离相等。
建立泰森多边形算法的关键是对离散数据点合理地连成三角网,即构建狄洛尼(Delaunay)三角网。建立泰森多边形的步骤如下。
(1)离散点自动构建三角网,即构建Delaunay三角网。对离散点和形成的三角形编号,记录每个三角形是由哪三个离散点构成的。
(2)找出与每个离散点相邻的所有三角形的编号,并记录下来。注意:对已构建的三角网中找出具有一个相同顶点的所有三角形即可,如图3.9所示。
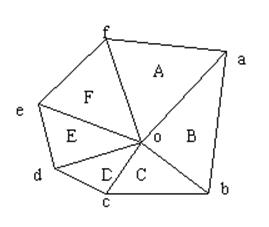
图3.9 泰森多边形的建立
(3)对与每个离散点相邻的三角形按顺时针或逆时针方向排序,以便下一步连接生成泰森多边形。排序的方法如图3.9所示。设离散点为o。找出以o为顶点的一个三角形,设为A;取三角形A除o以外的另一顶点,设为a,则另一个顶点也可找出,即为f;则下一个三角形必然是以of为边的,即为三角形F;三角形F的另一顶点为e,则下一个三角形是以oe为边的;如此重复进行,直到回到oa边。
(4)计算每个三角形的外接圆圆心,并记录之。
(5)根据每个离散点的相邻三角形,连接这些相邻三角形的外接圆圆心,即得到泰森多边形。对于三角网边缘的泰森多边形,可作垂直平分线与图廓相交,与图廓一起构成泰森多边形。
以上步骤可在编程软件环境中实现。
TIN是一种拓扑数据结构,它不仅存储每个数据点的(x,y,z)三维坐标值,而且存储三角网的拓扑特性,包括组成每个三角形的三个顶点(数据点)或边以及每个三角形的所有相邻三角形。每个三角形具有三个特性(包括:面积、梯度(或坡度)和方位),都可以作为TIN 的属性值存储在一个数据文件中,或在使用TIN时将它们计算出来。
采用距离变换生成Voronoi图的过程如图3.10所示。有点类似在水面扔几个石子,水纹扩展,显示变化的趋势。
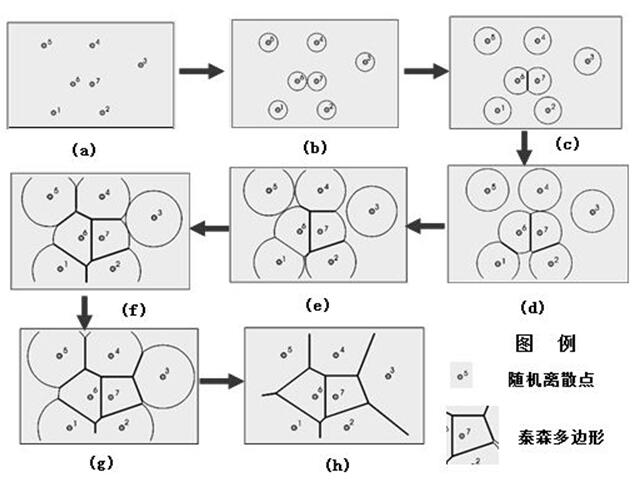
3.10 采用距离变换生成Voronoi图
TIN是根据不规则分布的数据点所构建的,很适合表示连续型面状实体,尤其对于复杂的、变化大的面状实体,表达比较逼真,效果较好。图3.11是由TIN表示的闽西根溪河流域的地势。
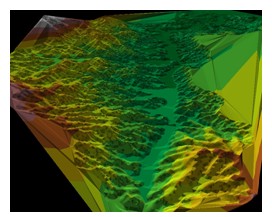
图3.11由TIN表示的闽西根溪河流域的地势图示
4、网络数据模型与数据结构
在现实世界中,若干线状要素相互连接成网状结构,资源沿着这个线性网流动,这样就构成了一个网络。它的基础数据是点与线组成的网络数据。在GIS中,网络(Network)是指一组相互连接的线状地理实体,如道路网、水系网、电力网、煤气和输油管道网等。在GIS中,网络数据模型本质上是矢量数据模型,它把网络看成是由结点(Node)和路径(Link)组成,并以结点和路径为单位描述网络的几何、拓扑和专题特征如图3.12所示。下面以道路网为例介绍网络数据结构。
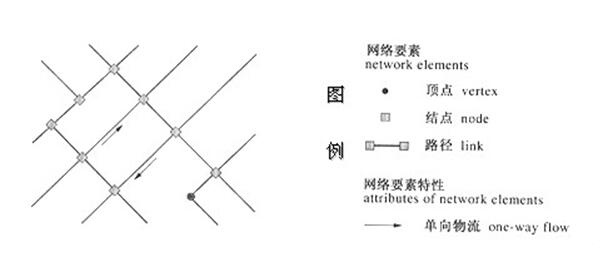
图3.12网络数据模型
GIS网络分析中最常涉及到的是道路网,如图3.13所示。每段路径有一个起始点和一个终结点(按数字化的顺序),这些信息都存储在表3.10中,每段路径的属性以及有关的阻强指标值存储在表3.11中,这些可能包括路段的长度、速限、车道数、允许的行使方向等。在表示允许的行使方向时,FT表示允许的方向是由起始点到终止点,TF表示由终止点到起始点,FT和TF标志着相应的路径为单行道,E表示双行道,N则表示该路径不允许车辆行使。
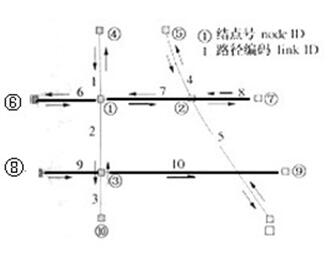
图3.13道路网信息
表3.10 路径——结点表
| 路径 Link# | 起始点 From_node# | 终结点 To_node# |
| 1 | 4 | 1 |
| 2 | 1 | 3 |
| 3 | 3 | 10 |
| 4 | 2 | 5 |
| …… | …… | …… |
表3.11 路径属性表
| 路径 Link# | 长度 Length | 起始点到终结点的时间 From_To time | 终结点到起结点的时间 To_From time |
| 1 | 850 | 2 | 1.5 |
| 2 | 1100 | 3 | 3 |
| 3 | 600 | 1.5 | 2 |
| …… | …… | …… | …… |
结点表示道路交叉口或路口,从某一路径来到一个路口可以一直往前走,向左转,向右转或作∪形转弯(180゜)折回来走。在一个路口可转弯的方向取决于路口道路的情况以及此路口的交通规则。在路口转弯所花的时间常称为转弯阻强(Turn Impedance),在一般情况下,它与转弯的方向有关。交通网中每段路径在其结点处所有允许的转弯方向及转弯阻强都存储在一个转弯类型表中,如表3.12所示。
表3.12 转弯类型表
| Node# | From link# | To link# | Angle(゜) | Time(Minutes) |
| 1 | 1 | 2 | 0 | 0.25 |
| 1 | 1 | 6 | -90 | 0.25 |
| 1 | 1 | 7 | 90 | 0.50 |
| 1 | 1 | 1 | 180 | 0.75 |
| …… | …… | …… | …… | …… |
| 2 | 0 | 0.00 | ||
| 2 | 90 | 0.50 | ||
| 2 | -90 | 0.25 | ||
| 0 | 0.00 | |||
| …… | ||||
| 3 | 90 | -1.00 | ||
| 3 | -90 | 0.25 | ||
| …… | …… | …… | …… | …… |
在过去30几年中,矢量数据模型是GIS中变化最大的方面。例如,ESRI公司在不同时期所开发的GIS软件都相对应着一种矢量数据模型,ArcView对应Shape-file,Arc/Info对应Coverage,ArcGIS对应Geodatabase。Shape-file和Coverage就是地理关系数据模型的代表,Geodatabase是面向对象数据模型的代表。矢量数据模型的演变是计算机技术发展和GIS市场竞争的结果。对用户来说,有许多新的概念和方法要学习。

