3.2  GIS数据结构（2）

                     

                    栅格数据结构表示法

栅格数据结构表示法以规则网格描述地理实体，记录和表示地理数据。具体说明如下。

一、栅格数据模型

栅格数据模型视地球表面为平面，将其分割为一定大小、形状规则的格网（Grid），以网格（Cell）为单位记录地理实体的分布位置和属性，如图3.14所示。

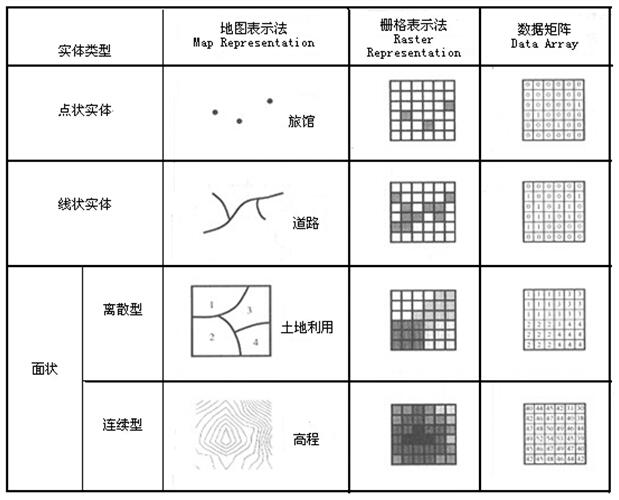
图3.14地理实体表示法

组成格网的网格可以是正方形、长方形、三角形或六边形，但通常使用正方形。使用这种栅格数据模型，一个点状地理实体表示为一个单一的网格或表示为单个像元；一个线状地理实体表示为一串相连的网格或在一定方向上连接成串的相邻像元的集合；一个面状地理实体则由一组聚集在一起且相互连接的网格或由聚集在一起的相邻像元的集合表示。每个地理实体的形状特征表现为由构成它的网格组成的形状特征。每个网格的位置由其所在的行列号表示，如图3.15所示，一般将格网定位为上北下南，行平行于东西向，列平行于南北向。在格网左上角的地面坐标、格网形状、格网大小以及比例尺已知的情况下，可以计算出每个网格中心所处的地理位置，从而确定地理实体分布的地面位置，计算地理实体的几何特征（如长度、面积等）。

由图3.15显示，栅格数据可以是一组数据矩阵，每个数据称为网格值，代表相应网格内地理实体的属性。根据属性值编码方案的不同，网格值可以为整数或浮点数，有些GIS还允许以文字作为网格值。在最简单的情况下，网格值为0或1，表示某一地理实体的存在与否。

图3.15 栅格数据模型的基本要素

栅格数据不明确地表示地理实体的拓扑特性，但有些特性可以通过计算获得。例如，若已知一个网格的行列坐标，就可以很容易地找到与它相邻的网格。类似地，根据网格的行列坐标和网格值，可以搜寻包含在一个面状实体内的另一个地理实体，等等以此类推。

栅格数据的精度在很大程度上取决于网格的大小。网格越大，精度越低；反之，网格越小，精度越高。栅格数据的精度对地理实体几何形状特征表示的详细性和精确性影响很大，一般地，实体特征愈复杂，栅格尺寸越小，分辨率愈高。但栅格数据量愈大（按分辨率的平方指数增加），计算机成本就越高，处理速度就越慢。不管网格有多小，由于每个网格只能拥有一个数值，因此，每个网格内有关地理实体属性变化的细节会全部丢失。而且，栅格数据总会在某种程度上会歪曲地理实体的细部特征，所以，在表示线状地理实体时少用。

当一个网格包含两种或两种以上不同类型的地理实体时，只能将它表示为其中一种类型。通常使用的网格赋值规则包括如下。：

（1）中心点法：选取位于栅格中心的属性值为该栅格的属性值。

（2）面积占优法：选取占据栅格单元属性值为面积最大者赋值。常用于分类较细、地理类别图斑较小的情景。

（3）重要性法：定义属性类型的重要级别，选取重要的属性值为栅格属性值，常用于有重要意义而面积较小的要素，特别适用于点、线地理要素的定义。

（4）长度占优法：定义每个栅格单元的值由该栅格中线段最长的实体的属性来确定。

二、栅格数据结构

栅格数据结构是以规则的阵列来表示空间地物或现象分布的数据组织，组织中的每个数据表示地物或现象的非几何属性特征。栅格数据结构的显著特点是属性明显，定位隐含，即数据直接记录属性的指针或数据本身，而所在位置则根据行列号转换为相应的坐标。栅格数据在计算机中可以有多种存储方式（或编码），主要包括完全栅格数据结构（栅格矩阵编码）和压缩栅格数据结构（如：游程编码、链编码（Chain Coding）、四叉树（Quadtree）等）。

1.完全栅格数据结构

完全栅格数据结构(将网格值按照网格的行、列排列顺序直接以一个栅格矩阵存储在一个计算机数据文件中，即将栅格数据看作一个数据矩阵，逐行（或逐列）逐个记录代码（也称直接栅格编码）。通常，这个文件具有一个文件标头部分，用以存放有关栅格数据模型基本要素方面的数据，包括行数、列数、网格大小、格网左上角或左下角的实际地面坐标等，或将这些数据单独存放到一个标头文件中，如图3.16所示。ArcView GIS空间分析的数字高程模型（DEM）就是使用这种栅格数据结构存储的。另外数字高程模型和卫星数字影像主要也采用这种数据结构。

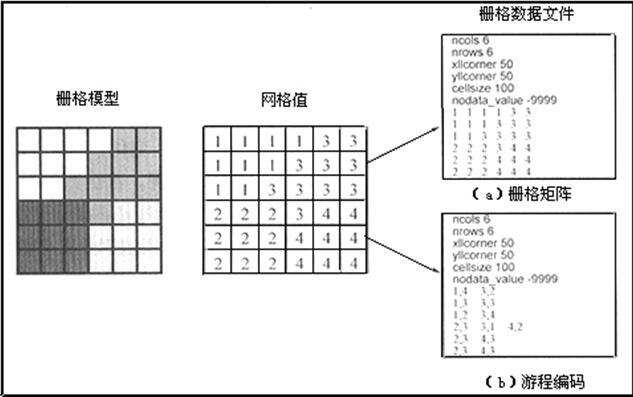
图3.16栅格数据结构

栅格矩阵要求存储所有的网格值，所产生的数据文件的大小取决于网格的行数和列数（m×n）。网格的大小对栅格数据量有很大的影响，即数据量随网格大小的改变呈平方变化。另外这种数据结构存储的网格值，冗余度较大。尤其对大量数据的栅格矩阵表达在存储上会占据大量的空间，为解决这个问题，人们提出数据压缩的方法，常见的有：游程编码、链编码和四叉树编码等。

2.压缩栅格数据编码

（1）游程编码

地理数据往往有较强的相关性，也就是说相邻像元的值往往是相同的。通过记录行或列上相邻的若干属性相同点的代码，可实现游程长度编码。具体方法：按行扫描，将相邻等值的像元合并，并记录代码的重复个数。如图3.17所示,其编码为A4 A1 B3A2 B2 A2 B2。若在行与行之间不间断地连续编码，则为A5 B3 A2 B2 A2 B2。区域越大，数据的相关性越强，使用游程长度编码，则压缩效果越佳。

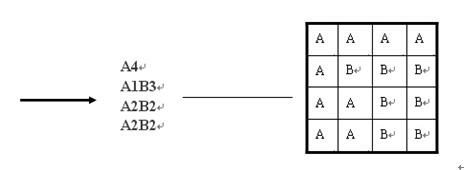
图3.17 游程长度编码

（2）链编码

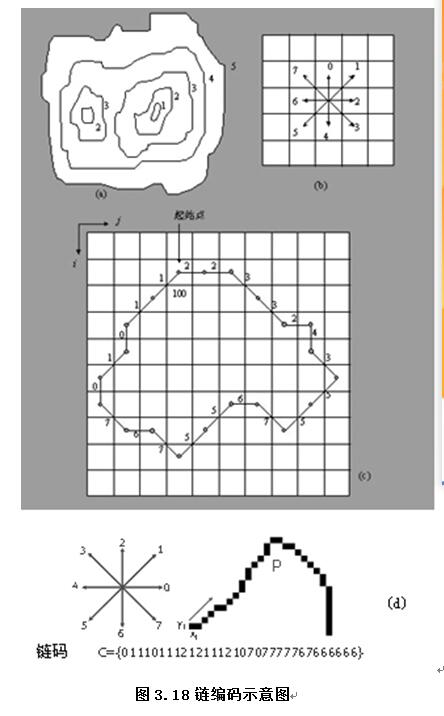
链编码（也称“弗里曼链码”）是用一系列按顺序排列的网格表示一个面状实体的分布界线，用以表示和存储面状实体的栅格数据。运用这种数据结构时，首先在面状实体的边界上选择一个起点，然后按逆时针或顺时针方向沿着边界记录前进的方向以及在该方向上移动的网格数目直到最后回到起点，如图3.18所示。其中图3.18（a）是原图，图3.18（b）代表8个方位（N,EN,E,ES,S……）的编码，图3.18（c）为栅格模型网格的数据编码。图3.18（d）为链编码。

（3）四叉树编码

四叉树（简称QT）编码的思路是把地理空间（特别是多边形区域信息）定量划分为可变大小的网格，每个网格具有相同性质的属性，它是最有效的栅格数据压缩编码方法之一。

四叉树结构的原理可以表述为：将二维区域按照四个象限进行递归分割（2ⁿ×2ⁿ，且n≥1），直到子象限的数值单调为止。凡数值（特征码或类型值）呈单调的单元，不论单元大小，均作为最后的存储单元。这样，对同一种空间要素，其区域格网的大小，随该要素分布特征而不同,四叉树结构在数据存储与检索方面效率很高。以图3.19表示四叉树的建立过程。

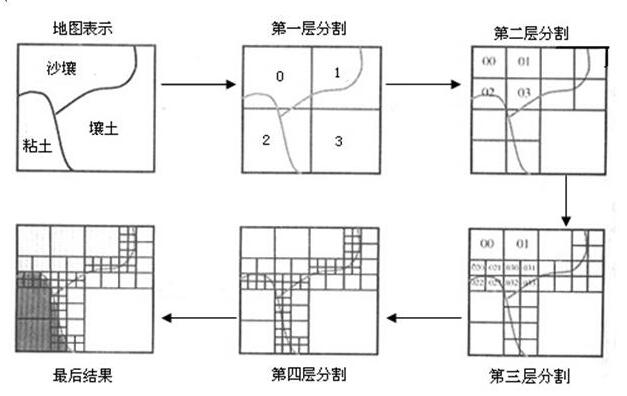
图3.19 四叉树结构的建立过程

同理，若对三维和四维数据结构而言，就有八叉树和十六叉树结构的编码。本书就不做介绍了。

四种栅格数据编码各有特点，比较见表3.13。总之，栅格数据模型用规则网格来覆盖整个空间数据。网格中的各个单元格数值与其位置上的空间特征相对应，而且单元格数值的变化反映了事物现象在空间上的变化。与矢量数据模型不同的是栅格数据模型在过去30几年中并未改变与其相关的概念或数据格式。有关栅格数据模型的研究目前已经集中在数据结构和数据压缩方面。在GIS软件中，虽可使用多种数据，但采用栅格格式居多，所以，对用户来说，理解栅格数据的存储和检索很重要。

表3.13栅格数据编码的特点

                   

栅格数据编码名称	特  点
直接栅格编码	将栅格数据看作一个数据矩阵，逐行（或逐列）逐个记录代码，这样存储的栅格数据包括了许多多余的数据
游程编码	通过记录行或列上相邻的若干属性相同点的代码来实现。压缩效率较高，叠加、合并等运算简单，编码和解码运算快。块码，采用方形区域为记录单元，是游程长度编码扩展到二维的情况
链编码	用一系列按顺序排列的网格表示和存储一个面状实体的分布界线
四叉树编码	l  容易而有效地计算多边形的数量特征，多用于数字影像处理   l  阵列各部分的分辨率是可变的，边界复杂部分四叉树分级多，分辨率也高，而不需要表示的细节部分则分级少，分辨率低。因而既可精确表示图形结构，又可减少存储量，效率高   l  直接栅格编码到四叉树编码及四叉树到简单栅格编码的转换比块式编码等其它压缩方法容易   l  多边形中嵌套不同类型小多边形的表示比较方便