基于栅格数据的GIS空间分析（1）

栅格数据特征和处理在前面已介绍过，这里主要介绍基于栅格数据的GIS空间分析原理。在栅格数据模型中，使用的是一种规则格网来覆盖研究空间，该格网的每个像元值对应于该单元格位置上空间现象的特征。换句话说，地理空间被划分为规则单元或像元，像元的大小则反映数据的分辨率。空间位置由像元的行列号表示，结构简单，计算效率高。可用于栅格数据分析的方法和技术很多，分析能在独立单元格、一组单元格或整个栅格全部单元格的不同层次上进行，而且多是在单元格的数值类型上分析。适于栅格数据表达的空间分析有空间一致性分析、邻近分析、离差、差量分析和影像分析等。目前主要有逐点运算、邻域运算、区域运算和广域运算四大类。栅格数据分析中的点、邻域、区域的概念如图5.27所示。

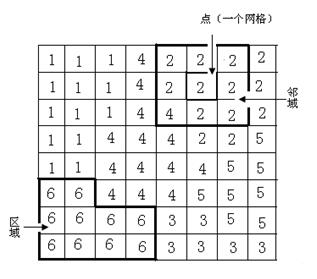
图5.27 栅格数据点、邻域、区域的图示

一、栅格叠加分析

有关叠置分析原理在5.1.3中介绍。栅格数据的叠加分析主要是逐点运算和区域运算。

（一）逐点运算

逐点运算的原理是以网格为单位，即逐个网格地进行栅格数据分析，逐点运算输出的网格值为同点输入网格值的函数。逐点运算可分为三种：数据的重新分类（Reclassification）、数值计算（Computation）、逐点叠置分析（Location_Specificoverlay Analysis）。

1.重新分类

重新分类运算是以一个栅格图层为输入，并根据一定的分类规则或逻辑运算规则，将每个网格值重新分类，输出的图层是一个新的栅格图层，即表示每个网格重新分类后的新值。重新分类运算主要应用包括以下几种。

（1）数据分离：即将某一类型的地理实体从一幅栅格图层中分离出来。通常是将一幅栅格图层转变为网格值为0或1的新栅格图层，1表示某类地理实体的存在，0则表示没有这类实体的存在。例如，只对某一地区森林分布所在地感兴趣，为此，可将一幅以栅格数据模型表示的土地利用图二值化，以1表示具有森林分布的网格，0表示非森林分布的网格，如图5.28（a）所示。数据分离可以说是栅格GIS中数据查询的一种方式。这个例子实际上是回答了“哪里有森林分布”的问题。

（2）数据简化：即将数据由较详细的分类分级简化为比较概括的分类分级，减少分类分级的数目。例如，将松树林、桉树林合并为森林，小麦、土豆合并为农作物，如图5.28（b）所示。

（3）数据分等：即将输入栅格图层中的每个网格值按等级划分，以一幅新的栅格图层输出每个网格的等级值。例如，对一幅表示土壤肥力指标的栅格图层进行重新分类，将土壤肥力指数划分为高、中、低三个等级，输出反映这三个等级土壤肥力的栅格数据，如图5.28（c）所示。

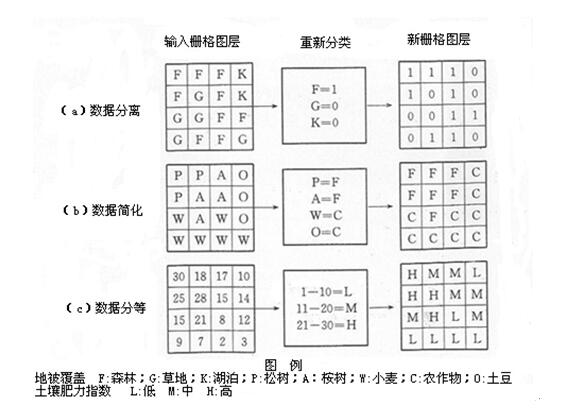
图5.28重新分类运算图示

2.数值计算

数值计算以一个栅格图层为输入，对输入的每个网格值作一定的数学运算，以一幅新的栅格图层输出运算的结果。GIS中用于栅格数据逐点数值计算的常用数学运算见表5.1。

表5.1栅格数据逐点分析中常用的数学运算

               

算术运算	加（＋）、减（－）、乘（×）、除（∕）、绝对值（abs）、整数（int）、float（浮点数）
指数、对数运算	乘方（exp）、对数（log）
三角函数	正弦（sin）、余弦（cos）、正切（tan）、反正弦（arcsin）、反余弦（arccos）、反正切（arctan）
幂	平方（sqr）、平方根（sqrt）、幂（pow）

 

例如：一个输入栅格图层记录以厘米为单位的月均降雨量，将其每个网格值乘以10，可以输出一个以毫米为单位表示月均降雨量的栅格图层，如图5.29（a）所示。以百分数表示的坡度转换成以度数表示的坡度图的数值计算如图5.29（b）所示。

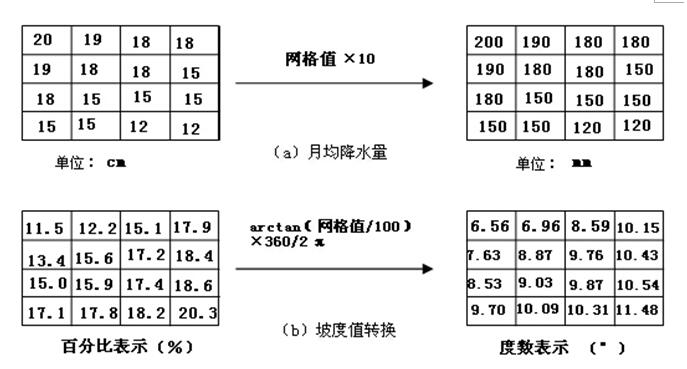
图5.29  数值计算示意图

3.逐点叠置分析

传统的地图叠置分析方法是先将参与分析的地图分别复制到透明片上，然后将这些透明片一层层叠置在透光桌上，通过目视分析各现象之间的联系或空间对应关系，再根据各现象属性之间的不同组合进行分类，勾绘出反映各现象组合特性分类的区域范围，最后，才制作一幅新的地图。可以基于GIS模拟上述手工地图叠置分析，并将这一过程自动化。GIS叠置分析是地理数据综合分析的一种地图分析方法，即将若干同一地区、不同专题的地图在统一的地表定位参照系统下叠置在一起，分析或模拟多种地表现象在空间上的相互联系，或进行某些现象的区域统计分析，主要的操作有“并”、“交”、“或”等。

在栅格GIS中，逐点叠置分析是对两个或两个以上的输入栅格图层中同一位置（行、列）上的两个或两个以上的网格值进行逻辑、规则、算术或统计分析运算，以一个新的栅格图层直接输出运算的结果，或根据运算的结果对网格进行分类，以新的栅格图层输出分类的结果。GIS中常用叠置分析的逻辑、规则、算术和统计分析运算见表5.2。

表5.2 GIS中常用于叠置分析的逻辑、规则、算术和统计分析运算

               

逻辑运算	与（AND）、或(OR)、异或(XOR)
规则运算	如果……那么……（IF…THEN…）、如果……那么……否则……（IF…THEN…ELSE）
算术运算	加（＋）、减（－）、乘（×）、除（∕）
统计分析	最大值（maximum）、最小值（minimum）、平均值（mean）、极差（range）、标准差（standard）、和（sum）、中数（median）、众数（mode）、多数（majority）、少数（minority）、多样化（diversity或variety）

 

在作逻辑叠置分析之前，通常是将输入栅格图层重新分类，转换为二值（0或1）栅格图层。对于逻辑与（AND）运算，如果两个输入栅格图层的对应网格值都为1，输出的相应位置上的网格值则为1；否则，输出的相应位置上的网格值为0，如图5.30（a）所示。对于逻辑或（OR）运算，如果两个输入栅格图层的对应网格值至少有一个为1，输出的相应位置上的网格值则为1，否则为0，如图5.30（b）所示。对于逻辑异或（XOR）运算，如果两个输入栅格图层的对应网格值中，其中一个为1，另一个为0，则输出的相应位置上的网格值为1，否则为0，如图5.30（c）所示，图5.31是属性叠加分析。

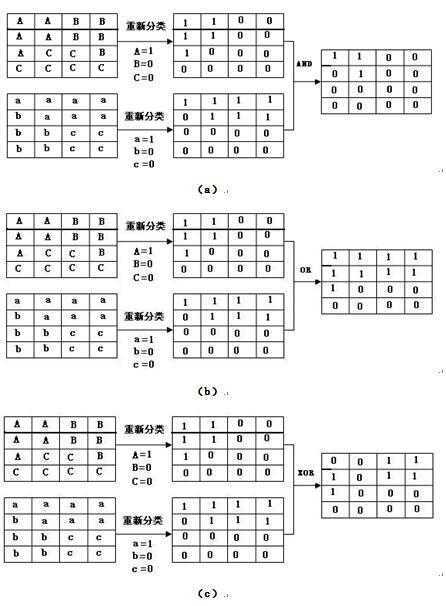
图5.30逻辑叠置分析

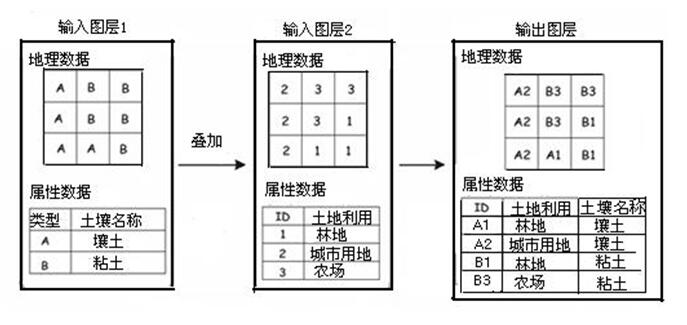
图5.31属性叠置分析

规则运算是运用“If（如果）…Then（那么）…”的条件规则，对输入图层中的网格值进行判断，如网格值满足“If”条件，就执行“Then”后面的运算或操作，输出运算、操作的结果。图5.32是一个规则叠置分析的例子。

栅格数据的逐点叠置分析将栅格图层看作变量进行多种数学运算，由此产生了地图代数（Map Algebra）的概念（Berry,1993）。运用地图代数，可以对栅格图层进行加、减、乘、除、乘方等运算，并以栅格图层为变量建立数学模型，模拟地理现象和过程（有关GIS应用模型详见第6章）。

除了上述叠置分析运算以外，还有一种称为组合(Combine)的算法，它不作任何数学和逻辑运算，而是以一个唯一值表示输入网格值的不同组合。例如：假设有两个栅格图层输入，其中一个表示1989年的土地利用分布，另一个表示2000年的土地利用分布，对这两个图层执行组合运算，结果将输出一个新的栅格图层，每个输出网格值为一个表示土地利用变化的唯一代码（如图5.33）。图5.34是闽西长汀2001年至2013年土地利用类型变化（2001a-2005a-2009a-2013a）系列图。

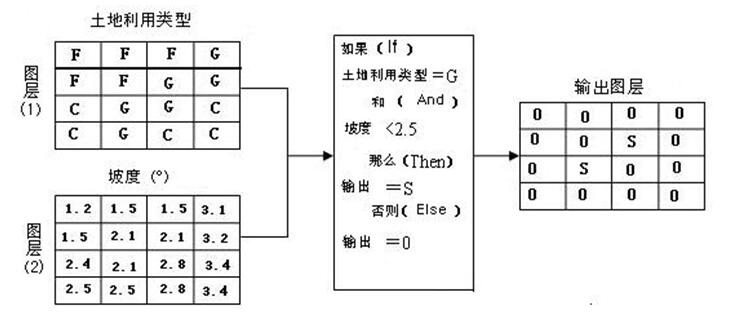
图5.32规则叠置分析

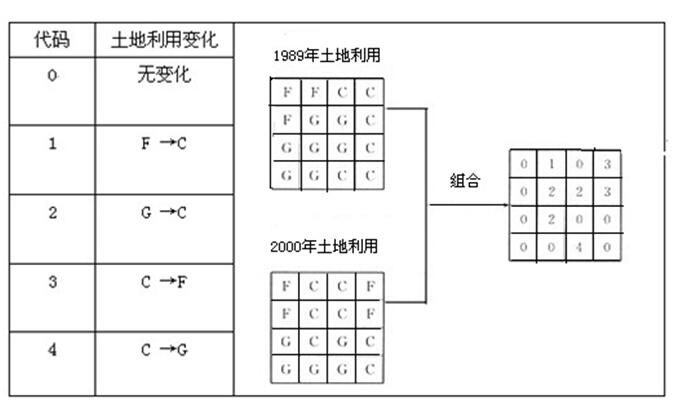
图5.33叠加分析中的组合运算

图5.34  闽西长汀土地利用类型变化系列图

在逐点叠置分析中有两个需要特别注意的问题。第一，若参与叠置分析的栅格图层的网格精度不一致，应当将它们统一到其中最差的网格精度。比如，两个用于叠置分析的栅格图层，一个网格精度为10m（即网格边长为10m），另一个为40m，在将它们叠置在一起之前，应对网格精度为10m的图层进行转换，如通过使用空间聚集运算将网格合并(稍后介绍)，使其网格精度降至40m。第二，在对栅格图层进行某一叠置分析运算时，需要理解每个参与叠置分析的栅格图层中网格值的数据类型，避免产生无意义的结果。例如，一个栅格图层以整数为代码表示土地利用类型（如1表示森林，2表示草地），另一个栅格图层以浮点数表示年均降雨量，对这两个栅格图层进行算术叠置分析是没意义的。

5.1.1.2 区域运算

一个区域可以是一组相邻接的网格，也可以是由若干相互不相连但具有相同属性值的网格组成。区域运算则是根据输入网格值的类别将全区划分为一系列区域，计算每个区域的几何特征，或根据包含在每个区域内的网格值计算输出网格值。在栅格图层中，一个区域由具有相同特性或属性值的网格组成。例如，全中国水稻种植区不连续地分布在全国各地，但它们可定义为同一个区域。区域运算是以区域为单位分析和操作栅格数据，主要有三组：区域单元识别、分区叠置分析和几何量测。

1．区域单元识别

该运算将同值的相邻接的网格组合成区域单元（相当于矢量模型中的一个多边形），并赋予每个区域单元一个唯一的识别码。例如在图5.35中，一个包含有三种森林类型的栅格图层经区域单元识别运算后，划分出五个区域单元，并赋予每一个区域单元不同的标识码。尽管松树林和栎树林分布于多处，但它们互不相连，因此，分别以不同的区域单元输出。这一运算主要用于涉及到要求对每一个区域单元进行逐一分析的GIS应用。

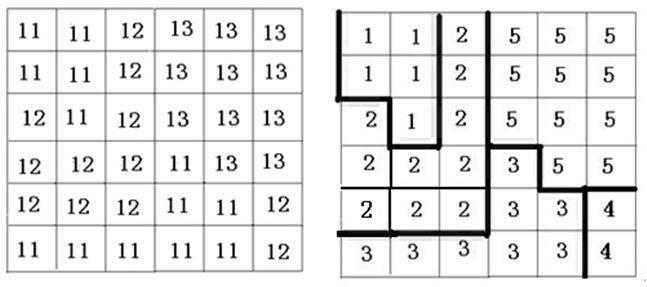
11－松树林， 12－榕树， 13－桉树

图5.35区域单元识别运算图示

2．分区叠加分析

分区叠加运算是以一个输入栅格图层中定义的区域为单位，对另一个输入栅格图层表示的地理数据作某种数学或统计计算，表达各区域内某种地理实体分布的数量特征。分区叠加分析与逐点叠加分析在概念上以及在分析应用的目的上是不一样的。逐点叠加分析是对多个输入栅格图层中相同位置上的网格值进行逻辑、规则、算术和统计运算，以建立多种地理实体在空间上的相互联系，或根据多种要素分析、模拟某一现象的过程。分区叠加分析则主要是根据表示在一个输入栅格图层上的区域边界，对位于每一区域范围内的另一输入栅格图层中的网格值逐个区域地进行运算，用于分区或分类统计。例如，将一个表示某省县级行政区划的栅格图层与一个表示该省土地利用分布的栅格图层叠加起来，可以分析每个县区范围内主要的土地利用类型，以及各类土地利用所占的面积和比例。又如，在市场分析中，常将一个表示区级行政界线的栅格图层与表示人口数据的栅格图层叠加起来，统计每个区人口的大小、家庭的平均收入、年龄结构和教育程度等。表5.1中列出的统计分析运算都可运用于分区叠加分析。图5.36给出了一个分区叠加分析的例子，该例将森林分布栅格图层和高程栅格图层叠加起来，计算每类森林地的平均高程，输出栅格图层中的每个网格值为其所属森林地类型的平均高程值。在一些GIS中，分区统计叠加分析并不产生新的栅格图层，只是以图表的形式输出分区统计的结果。如在如图5.37所示的例子中，将土地利用图层和洪水淹没区图层叠加起来，以土地利用类型为区域单位，统计出各类土地利用受淹的面积，以柱状图输出统计分析的结果。

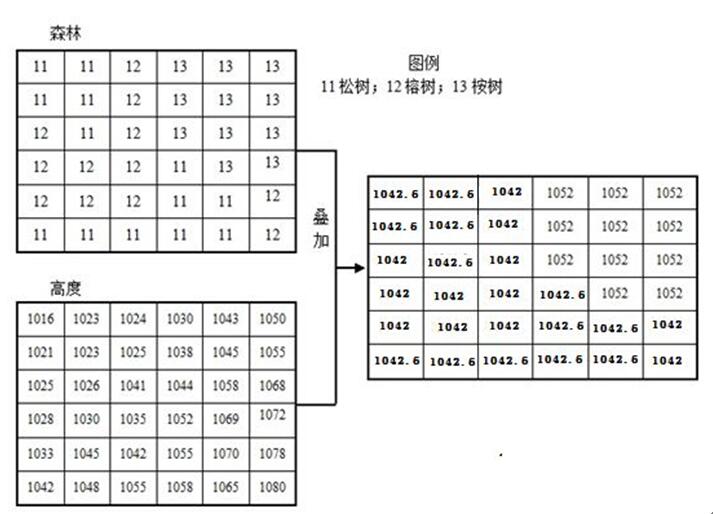
图5.36分区叠加分析

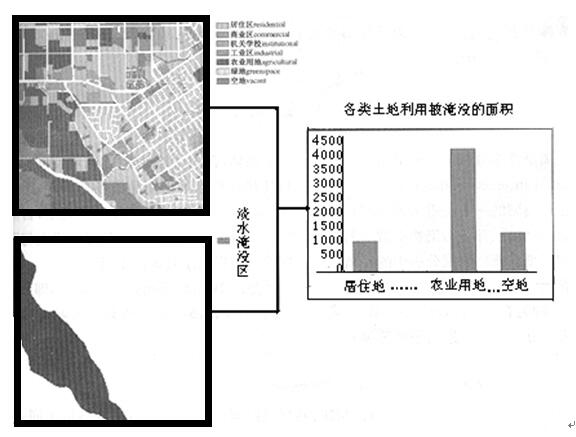
图5.37以土地利用类型为区域单元，统计各类型受淹面积

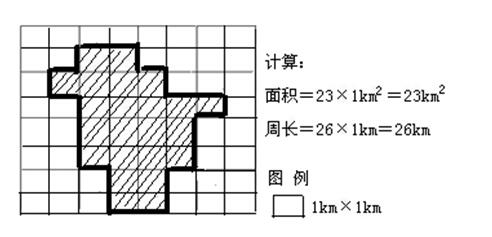
图5.38区域面积和周长的计算

 

3．几何量测

区域运算中的几何量测主要是区域面积、周长、宽度和形状特征的计算。在一幅栅格图层上，一个区域的面积是位于该区域范围边界内所有网格面积的总和，可由位于区域内网格的总数乘以一个网格的面积计算获得。一个区域的周长等于形成该区域边界的外围网格边的总数乘以一个网格的边长，如图5.38所示。如果一个区域由若干个离散分布的区域组成，则它的周长为所有这些区域周长的总和。一个区域的宽度定义为该区域内所能包含的最大圆的半径。一个区域的形状特征通常以其周长和面积的比率作定量描述。例如：在景观生态学（Landscape Ecology）中，对景观类型的定量表达，常应用区域几何特征来分析。

相对而言，栅格数据的逐点叠置分析在计算上简单、快速，因此，在涉及到许多要素的分析和模拟时，通常使用逐点叠置分析。

值得一提，GIS中的地图叠置分析技术实现了空间信息综合分析手段的自动化，避免了手工地图叠置分析过程中可能产生的错误和误差，它将分析、制图、统计和计算等几个环节自动地连接了起来，这是常规方法所无法实现的。它和地理数据库相结合，还可以将分析结果返回到数据库中，为数据库补充新的数据。可以说叠置分析是GIS最常用的分析手段之一。

但同是叠置分析，不同的数据操作方法不同，应注意概念的区分。例如：

（1）图形叠置（视觉叠置）是将一个被选主题的图形所表示的专题信息放在另一个被选主题的图形所表示的专题信息之上。

（2）栅格自动叠置：是基于网格单元的多边形叠置，是一个简单的过程，因为区域是由网格单元组成的不规则的块，它共享相同的一套数值和相关的标注。毫无疑问，网格单元为基础的多边形叠置缺乏空间准确性，因为网格单元很大，但是类似于简单的点与多边形和线与多边形叠置加的相同部分，由于它的简单性，因此可以获得较高的灵活程度和处理速度。

（3）拓扑矢量叠置：是指如何决定实体间功能上的关系。如定义由特殊线相连的左右多边形，定义线段间的关系去检查交通流量，或依据个别实体或相关属性搜索已选择实体。它也为叠加多个多边形图层建立了一种方法，从而确保连结着每个实体的属性能够被考虑，并且因此使多个属性相结合的合成多边形能够被支持。这种拓扑结果称作最小公共地理单元(LCDU)。

（4）矢量多边形叠置：则指点与多边形或线与多边形叠置使用的主要问题是，线并不总是出现在整个区域内。解决该问题的最强有力的办法是让软件测定每组线的交叉点，这就是所谓的结点。进行矢量多边形的叠置，其任务是基本相同的，除了必须计算重叠交叉点外，还要定义与之相联系的多边形线的属性。

（5）布尔叠置：是一种以布尔逻辑（AND、OR、XOR、NOT）为基础的叠置操作。栅格数据一般可以按属性数据的布尔逻辑运算来检索，这是一个逻辑选择的过程。

二、栅格缓冲分析

缓冲区原理曾在5.1.2章节介绍，缓冲区分析包括缓冲区的建立及区域分析，它首先是对要素根据缓冲条件，建立缓冲区，然后将这个缓冲区图层与其他图层进行诸如叠置分析、网络分析、服务设施查找等其他分析操作，得到所需要的结果，以便为某些分析或决策提供依据。实现栅格数据缓冲区分析例子见图5.39，即栅格多边形A，设定缓冲d的距离后，生成多边形缓冲区B。

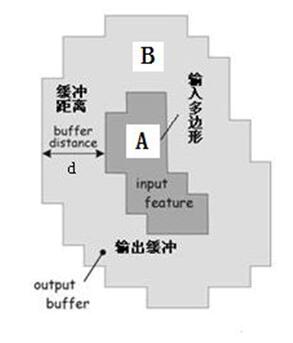
图5.39栅格多边形的缓冲区

三、栅格邻域分析

栅格数据邻域分析主要基于邻域运算。它以一个栅格图层为输入，根据每个网格周围某一邻域内所有网格值计算输出网格值，并产生一个新的图层，即邻域运算输出的每一个网格值为该网格邻域内所有输入网格值的函数。因此，在运用邻域运算计算每个网格的新值时，首先要定义一个邻域。一个待计算的网格称为焦点网格（Focal Cell），其邻域所包含的网格称为邻域网格（Neighbouring Cell）。一个网格的邻域（Neighbourhood）是根据一定的形状和大小定义的，它可以是一定大小的以该网格为中心的正方形，也可以是以该网格为圆心的圆（Circle）、圆锥（Wedge）或圆环（Ring）。最常用的邻域则由围绕焦点网格最邻近的四个网格或八个网格组成，如图5.40所示。

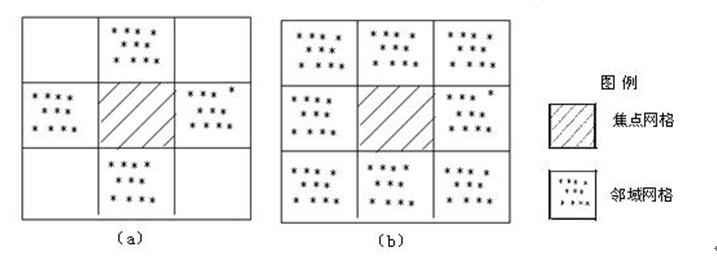
图5.40 网格邻域（a）和8网格邻域（b）

一个焦点网格及其邻域组成的区域称为一个窗口（Window）。邻域是指“具有统一属性的实体区域或者焦点集中在整个地区的较小部分实体空间”，邻域包括直接邻域和广域邻域，邻域分析就是在特定的实体空间中发现其属性的一致性。

（一）直接邻域分析

直接邻域运算包括三组：空间聚焦、过滤、坡度和坡向计算。

1．空间聚焦分析

栅格数据的空间聚集运算实际上是一个地图综合的过程，运算时用较大的网格对栅格数据重新采样（Resampling），以减少网格数量、降低栅格数据的空间精度。空间聚集运算不是对栅格数据进行压缩，而是以较大的网格表示同一地区。该运算采用一定大小的矩形窗口或邻域计算，窗口一般与输出网格等大，窗口越大，综合程度就越高，有关地理实体的细节也就丢失得越多。输出网格值的计算主要有三种方法：①中心网格值法（Central _Cell Method），以位于窗口为中心的输入网格值为输出网格值；②平均值法（AveragingMethod），计算窗口内所有输入网格值的平均值，以此作为输出网格值；③中数法（MedianMethod），以窗口内所有输入网格值的中数（Median）为输出网格值，如图5.41显示了空间聚集运算的三种方法（将6×6的栅格图层转换成2×2的栅格图层）。

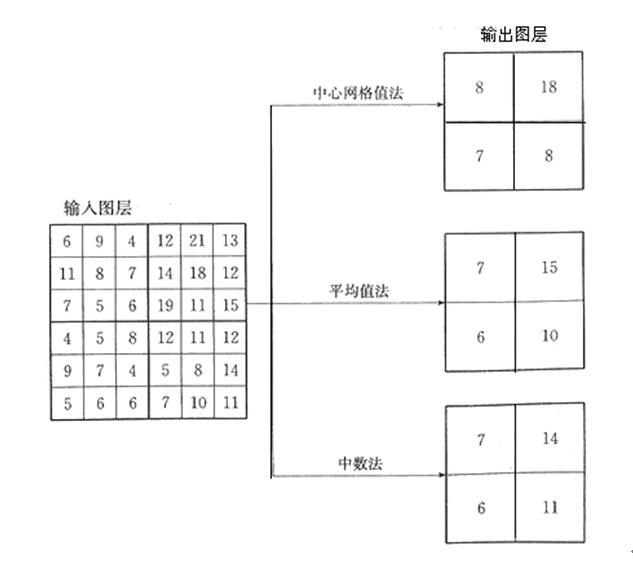
图5.41空间聚集运算法图示

栅格数据的空间聚集是环境研究中地理数据分析的一个重要过程。通常，环境研究中的地理数据是以适合于局部地区分析的较大比例尺采集的，通常需将它们综合、简化，转换成较小比例尺的数据，以适合于区域性和全球性分析的需要。

2．过滤分析

过滤运算（Filtering）运用一个移动窗口（Moving Window），以每个输入网格为焦点网格，逐网格地对以移动窗口定义的邻域中所有网格值进行特定的运算，计算每个网格的新值，如图5.42所示，典型的移动窗口为3×3或5×5矩形。过滤运算是将统计分析方法运用于移动窗口中的焦点和邻域网格值，计算出焦点网格的输出值。因此，过滤运算又称为邻域统计分析（Neighbourhood Statistics Analysis）。图5.43给出了示例，这些例子使用3×3矩形移动窗口，图中只显示了绘有晕线的网格输出值。

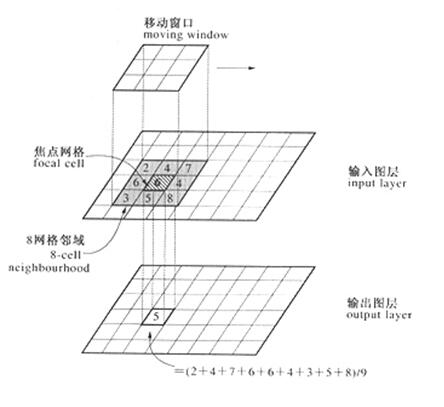
图5.42 邻域运算中移动窗口的概念

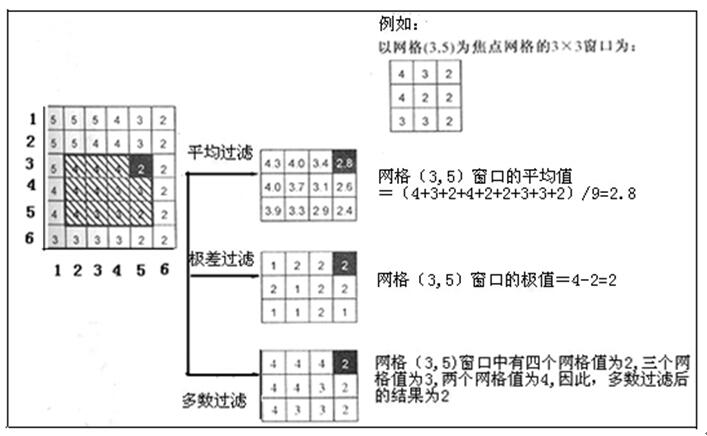
图5.43 栅格数据的过滤运算案例

（1）在平均（Mean）过滤运算中，当移动窗口从一个焦点网格移到另一个焦点网格时，计算窗口内网格值的平均值，并将它赋给窗口包含的焦点网格。平均过滤运算是对输入数据的简化，即缩减了输入网格值之间的差异，从而达到了图形的“平滑”效果，常用于影像处理中噪音的消除。

（2）极差（Range）过滤运算是指计算移动窗口中网格值的极差，并将其赋予相应的焦点网格，大的极差值意味着窗口中存在着一个类型或级别边界，因此，极差过滤运算在影像数据处理中常用于边缘增强（Edge Enhancement）。

（3）多数（Majority）过滤指的是在焦点网格内，计算占有网格值的数，以最多者为选取目标。

总之，过滤运算对于突出栅格影像中的线状实体特别有用，常用于分析水系、增强道路网影响、突出水域、植被、土壤和土地利用类型边界等。

3．坡度和坡向分析

根据基于栅格数据结构的数字高程模型(Digital ElevationModel，简称DEM)或栅格高程数据（Grid）来提取坡度和坡向，既是基本地形要素提取分析，又是属于邻域运算。数字高程模型不仅包含高程属性，还包含其它的地表形态属性，如坡度、坡向等。DEM通常用于地表规则网格单元构成的高程矩阵表示，广义的DEM还包括等高线、三角网等所有表达地面高程的数字表示。

利用规则格网模型(是最主要的形式, 如 GRID)、等高线模型、不规则三角网模型(TIN)、层次模型（如金字塔（Pyramids)）等可以构建DEM，这些模型各有优缺点，可根据实际应用加以选择，比较见表5.3。

表5.3  几种生成DEM的模型比较                             

模型	优点	缺点
规则格网模型	l  规则格网的高程矩阵，可以很容易地用计算机进行处理，特别是栅格数据结构的地理信息系统；   l  还可以很容易地计算等高线、坡度坡向、山坡阴影和自动提取流域地形；   l  为DEM最广泛使用的格式	l  不能准确表示地形的结构和细部格网；   l  数据量过大，给数据管理带来了不方便；   l  通常要进行压缩存储
等高线模型	直观，便于理解	l  只表示离散的数据，不能表示连续的数值或面状色彩填充地物特征；   l  不便于坡度计算、地貌晕渲等
不规则三角网模型(TIN)	l  减少规则格网方法带来的数据冗余   l  在计算（如坡度）效率方面有优于纯粹基于等高线的方法   l  利用复杂地形的表达	l  在地形平坦的地方，存在大量的数据冗余；   l  在不改变格网大小的情况下，难以表达复杂地形的突变现象；   l  某些计算，如通视问题，过分强调网格的轴方向
层次模型	l  数据简单；   l  顺序查询	l  因层次的数据导致数据冗余；   l  自动搜索的效率低, 例如搜索一个点可能先在最粗的层次上搜索，再在更细的层次上搜索，直到找到该点

 

在地理信息系统中，DEM是建立数字地形模型的基础数据，其它的地形要素可由DEM直接或间接导出，这种数据，称为“派生数据”，如坡度、坡向等。

在使用栅格高程数据时，每个网格的坡度和坡向是运用3×3的移动窗口来计算的。根据窗口内所使用的邻域网格数目以及分配给邻域网格高程值权重的不同，坡度和坡向的计算方法也有所不同，主要有如下三种：

（1）四网格邻域计算法

假设四个邻域网格的高程分别为E₁，E₂，E₃，E₄，网格边长为a，焦点网格为C，则C的坡度S可（5.20）式计算。

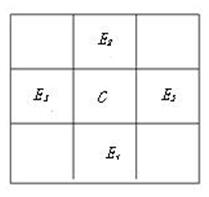
                                                             图5.44 四网格邻域算法

根据如下规则，可计算C坡向A。

当S等于0时，令A= －1，即C为平缓坡，坡向无定义；

当S不等0时，

①如果d_x=0，且d_y小于0，那么A=180°(南)；

②如果d_x=0，且d_y大于0，那么A=360°(北)；

③如果d_x大于0，那么A=90°－D；

④如果d_x小于0，那么A=270°－Ｄ。

例如：图5.45给出了一个栅格高程数据的3×3窗口，每个网格高程值以m为单位，网格边长为50m。

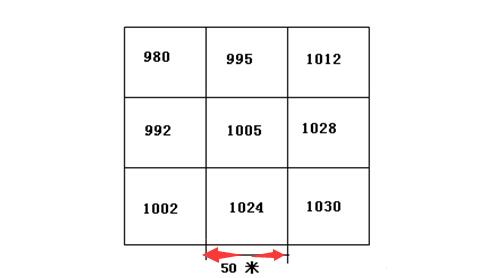
图5.45 格网高程数据的窗口

根据四网格邻域计算法可计算出该窗口中心网格（即焦点网格）的坡度、坡向如下：

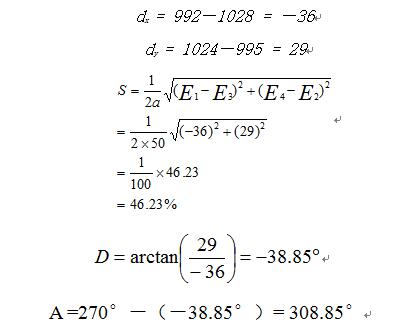
（2）八网格邻域计算法：

该方法采用八网格邻域（Sharpnack and Atkins,1969）。如图5.46所示。

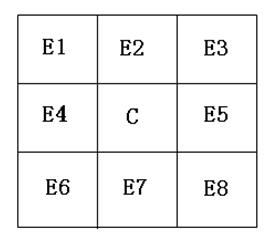
图5.46八网格邻域及其高程

假设八个邻域网格的高程分别为E₁，E₂，E₃，E₄，E₅，E₆，E₇，E₈，网格边长为a，则焦点网格C的坡度S为：

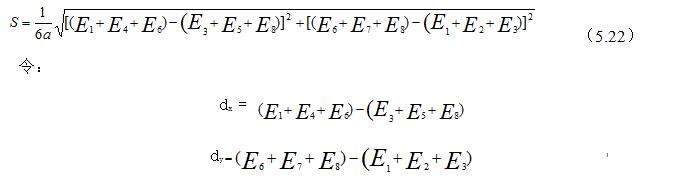
根据图5.45所给的数据，利用八网格领域（5.22）式计算，也可计算出D和A。

计算过程如下：

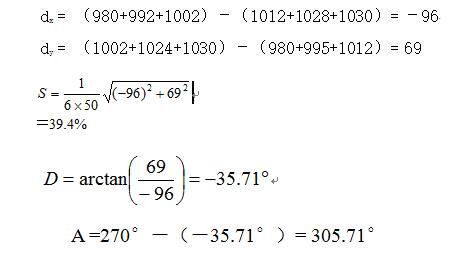
（3）八网格邻域加权计算法

八网格邻域加权方法与八网格邻域方法类似，它们采用相同的邻域定义,如图5.46所示，但加权计算法赋予四个角落邻域网格的权重值为1，其他邻域网格的权重值为2，并以(5.22)式计算焦点网格C的坡度（Horn,1981）S为：

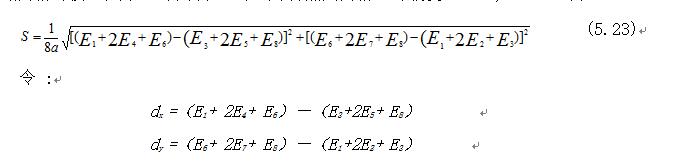
比较基于栅格数据的三种方法，可以看出坡度和坡向计算结果有一定的差值。用户在具体应用时可根据其精度要求，选择不同的方法。

基于ArcView 和ArcGIS的地形坡度和坡向提取分析都是使用八网格邻域加权计算法根据栅格数据计算坡度和坡向的。图5.47显示了闽西根溪河流域的坡度和坡向分级图。

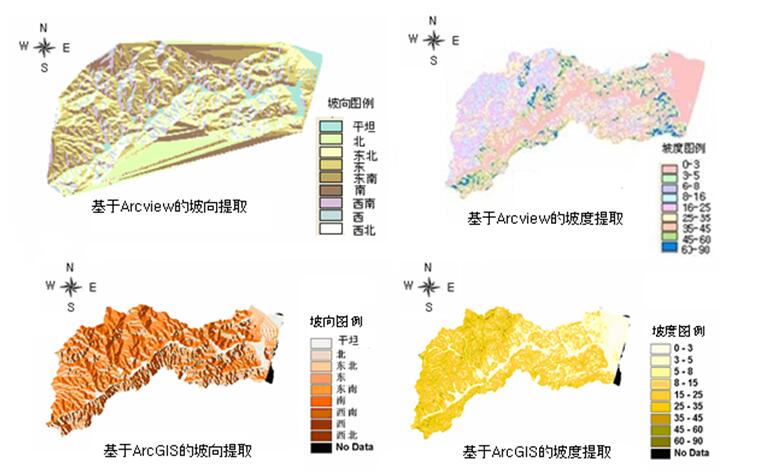
图5.47由栅格高程数据计算的坡度和坡向

坡度和坡向是描述地形特征的两个重要要素。尤其是坡度的应用非常广泛，例如：①根据坡度起伏变化，确定崩塌、泥石流区域或严重的土壤侵蚀区，作为灾害防治与水土保持工作的基础；②对于缓坡或平坦区域，通过提取，可为大型商业中心或房屋建筑选址。

（二）广域邻域分析

栅格邻域分析原理除了应用直接邻域运算外，还可应用广域运算。广域运算超出四或八邻域范围，有时甚至是全幅所有的输入网格值来计算输出网格值，主要涉及到与距离有关的分析（如接近程度（Proximity）、连接状况（Connectivity、通视情况分析(Intervisibility)等）。

距离是许多分析应用中最基本的要素之一。例如:在人文地理学中，常将空间相互作用模型（Spatial Interaction Model）应用于选址、人口迁移分析和零售商品市场分析等，距离是空间相互作用模型的一个关键参数。在自然资源和环境研究中，自然火灾蔓延、病虫害传播、环境污染物扩散等的模拟，以及野生动物栖息地分析都需要建立与距离有关的空间模型（详见第6章）。栅格数据分析中的距离运算为这些应用提供了基本的工具。

在栅格数据分析中，距离的计算有两种，一种是简单距离（Simple Distance）即平面直线距离；另一种为有效距离（Effective Distance），即将在某段距离上某些或某种影响通行的障碍考虑进去，如地形障碍、道路条件等。

1、简单距离

两个网格之间的简单距离以它们之间的直线距离计算。如果两个网格位于同一行，它们的距离等于它们列数之差的绝对值乘以一个网格的边长；如果两个网格位于同一列，它们的距离等于它们行数之差的绝对值乘以一个网格的边长；如果两个网格既不在同一行，又不在同一列，它们之间的距离则由勾股定理（Pythagorean Theorem）计算。

栅格GIS中简单距离运算主要有两种。第一种运算是计算一组表示某一类型地理实体的网格，称为起始网格，与其他所有网格之间的距离，其输出的栅格图层上的每个网格值为距起始网格的距离值，将这些网格值以一定的分级方法划分成若干等级，输出的地图可表示为环绕起始网格的等距离带。这样的图通常称为接近程度图（Proximity Map），它反映了区域中每一点到某一类地理实体的接近程度。如图5.48是福州居民点距离医疗机构的接近程度图。若将接近程度图重新分类，将距起始网格的距离小于或等于某一距离值d的网格值置1，而大于d的网格值置0，输出的地图将表示出环绕起始网格、宽度为d的缓冲带（Buffer）。形成缓冲带是GIS的一个重要功能，具有很多方面的应用。例如，在河流两岸建立一定宽度的缓冲带，禁止缓冲带内植被的砍伐，以防止土壤的侵蚀、保护河堤；在高速公路两旁建立一定宽度的缓冲带，以显示交通噪声高于一定程度的区域；在危险设施周围建立一定宽度的缓冲带，作为安全警戒线。

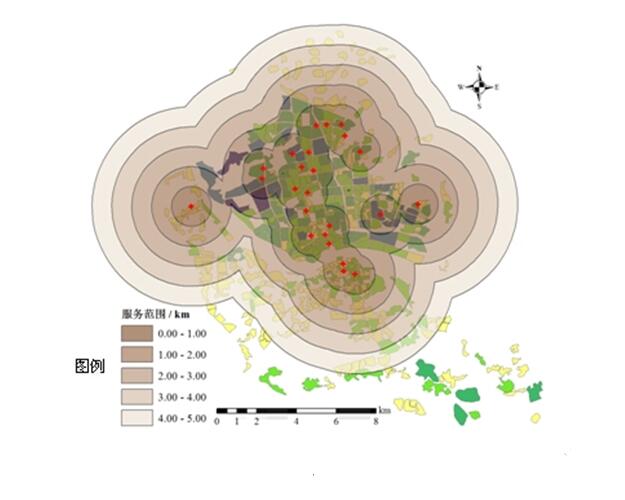
图5.48 福州市区居民点到医院机构接近程度图

栅格GIS中的第二种运算是根据距离将每一个网格分配给一组指定的地理实体中最接近的一个。

2、有效距离

有效距离运算是根据影响和限制不同地点之间运动的障碍来计算距离的。例如，从山脚一点步行到山顶的距离并不是这两点之间的水平直线距离，它受到坡度变化或地形起伏的影响，也可能因为湖泊或悬崖的存在，需绕道而行，从而增加了行走的距离。又如，一个送货员开车送货，他所关心的不是整个送货路线的长度，而是所花的时间。开车送货的时间不仅取决于路线的长短，也取决于道路的状况、交通条件和开车的时速限制等。有效距离可以长度为单位计算，也可以时间、费用等为单位计算。再如，在一个森林管理区，估算消防人员从某一消防站到达区内任何一点所需的时间，以应付森林火灾发生的可能事件，这不仅要计算消防车在公路上行驶的时间，还要估算消防车越野行驶的时间，因此，消防人员到达某一地点所需的时间必须考虑到土地覆盖的类型和地形条件。消防车穿过平缓草地的速度很快，通过坡度较陡的森林地段将会很慢，深水河流和悬崖则不能通过。将在一段距离上影响、减缓运动速度或增加运行费用的因素称为相对障碍（Relative Barrier），如不同类型的土地覆盖、地形坡度、道路条件等等；将完全阻挡运动的因素称为绝对障碍（Absolute Barrier），如悬崖、湖泊、河流等。从一点到另一点的有效距离是这两点之间存在的障碍影响的函数。如图5.49所示为有效距离运算的示例。

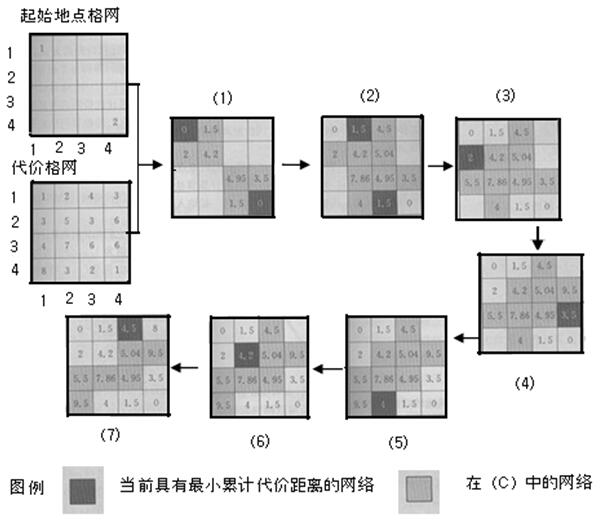
图5.49 有效距离计算示例

在栅格GIS中，有效距离的计算需要两个栅格图层，一个表示距离计算的起始地点（表示为一组或几组网格），另一个表示相同区域内通过每个网格的障碍的影响（如通过每个网格所需的时间）。后者常称为代价格网（Cost Grid），障碍的影响又称为代价（Cost），表示通过一个网格时，由某种或某些障碍所带来的费用、附加的时间、能量的消耗或通行的难易程度等。由一个网格到同行或同列的另一组邻网格的有效距离为这两个网格代价的平均值；由一个网格到对角的另一组邻网格的有效距离为它们代价的平均值乘以1.41421。如使用如图5.49所示中的代价格网，可以计算格网（1，1）到格网（1，2）的有效距离：

（1+2）/ 2 =1.5

格网（1，1）到格网（2，2）的有效距离为：

[ (1+5 ) / 2 ] × 1.41421=4.2426

如果一段路径由一组若干个相邻网格连接而成，那么它的有效距离为每个相邻网格之间的有效距离累加起来的总和，称为累计代价距离。任意两点之间可由不同的路径相连，它们之间的有效距离为所有可能路径中的最短有效距离，称为最小累计代价距离（Least Accumulative Cost Distance）。栅格GIS中的有效距离运算计算从起始地点到区域内其他每个网格的最小累计代价距离，将它们以一个新的栅格图层输出，其算法可描述如下：

（1）将起始地点所在网格的有效距离置0，逐一计算起始网格到其每个相邻网格的有效距离，这些有效距离即为起始网格到这些相邻网格的累计代价距离。然后，将这些相邻网格组成一个集合{C}。

(2)从{C}中取出累计代价距离最小的网格，设这一最小累计代价距离为d_min，逐一计算这些网格到其所有相邻网格的有效距离，将这些有效距离加上d_min，即得每个相邻网格沿某一路径自起始地点的累计代价距离。如果其中某相邻网格已存入于{C}中，这就说明该网格可从另一个不同的路径到达起始网格，比较当前计算的该网格的累计代价距离与其先前计算获得的累计代价距离，将较小的累计代价距离赋给此网格。待所有上述相邻网格的累计代价距离计算完毕，将它们加入{C}；

（3）重复第二步，直到获取所有网格到起始地点的最小累计代价距离。

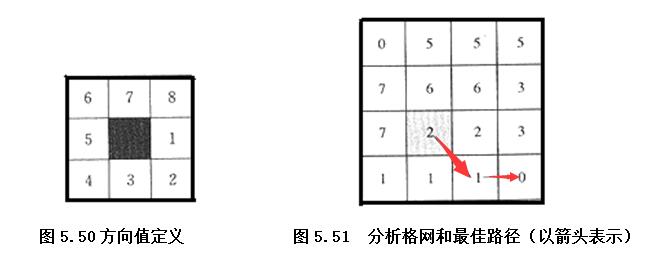
在某些GIS软件中，有效距离运算还可同时输出一幅方向格网（Direction grid），每个网格的方向值指明它应当走向哪一个相邻网格，以便以最小累计代价距离返回到起始点。方向格网上的方向值以1到8的数字表明相邻网格的位置,如图5.50所示，1表示右边的相邻网格，2表示右下方的相邻网格，3表示正下方的相邻网格，4表示左下方的相邻网格，5表示左边的相邻网格，6表示左上方的相邻网格，7表示正上方的相邻网格，8表示右上方的相邻网格，0表示起始网格。在方向格网上，自一网格出发，通过跟踪相应的相邻网格直至起始地点，可以寻找出该网格与起始地点之间的最小累计代价距离路径，即最佳路径。图5.51显示了使用图5.49中的数据产生的方向格网，并据此寻找出一个网格到其中一起始地点的最佳路径。最佳路径是GIS中刻画两点之间连接状况的主要手段。

3、通视分析

通视分析是根据地形高程数据判断任意两点之间是否相互通视（Intervisibility）。GIS中主要有两种通视情况分析运算，一种是视线分析（Line of Sight），另一种是视域分析（Viewshed）。

（1）视线分析

视线分析是判断从一个观察点能否看到一个给定目标，并判断在观察方向线上有无遮蔽视线的山体或其他障碍物。从观察点到目标点作一条视线，如果视线高出地形剖面线，这两点就是相互通视的（见图5.52）。由于通视情况受到观察点高度和目标高度的影响，视线分析通常考虑观察点和目标的平均高度。根据这一原理，还可以在观察点和目标点之间的地形剖面线上划分出可见区和不可见区（见图5.52），从而识别出那些地形部分可以观察得到，那些观察不到。在GIS中，视线分析使用数字高程模型（DEM），它允许用户在DEM上确定观察点和目标点的位置，当用户由观察点向目标点画出视线以后，GIS即可判断这两点是否通视，并在视线上标出可见区和不可见区部分。

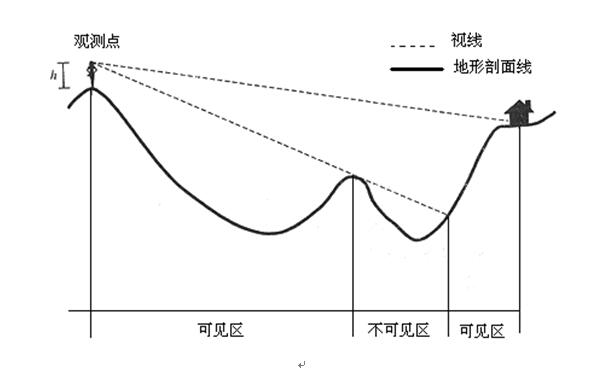
图5.52  视线分析

（2）视域分析

视域分析以视线分析为基础，以研究区域内的每个网格为目标点，从若干个指定的观察点判断每个网格是否与它们通视，根据判断的结果将网格划分成两大类：可见区和不可见区。有些GIS系统还根据可通视的观察点数目，将可见区划分为一观察点可见区、两观察点可见区等。该运算以两个图层为输入，一个表示观察点位置，另一个为DEM。

计算基于规则格网DEM的可视域的简单方法：就是沿着视线方向，从视点开始到目标网点计算与视线相交的网格单元（边或面），判断相交的网格单元是否可视，从而确定视点与目标点之间是否可视。

通视情况分析有着广泛的应用。例如，在野外工作中选择观察点的位置时，可帮助了解观察目标的通视情况；在地形分析中，能帮助确定从某一地点、某一角度可以看到哪些地形景观，这类信息可用于土地开发项目的景观影响评价、房地产估价、电讯传输线路的设计、沿河或沿路风景好坏质量的评价等。