-
1.1作者简介
-
1.2本书翻译团队与主译人简介
-
1.3内容提要
-
1.4译者序
-
1.5前言
-
1.6经济学与互联网
-
1.7第一编 基本概念
-
1.7.1第1章 经济学基础知识
-
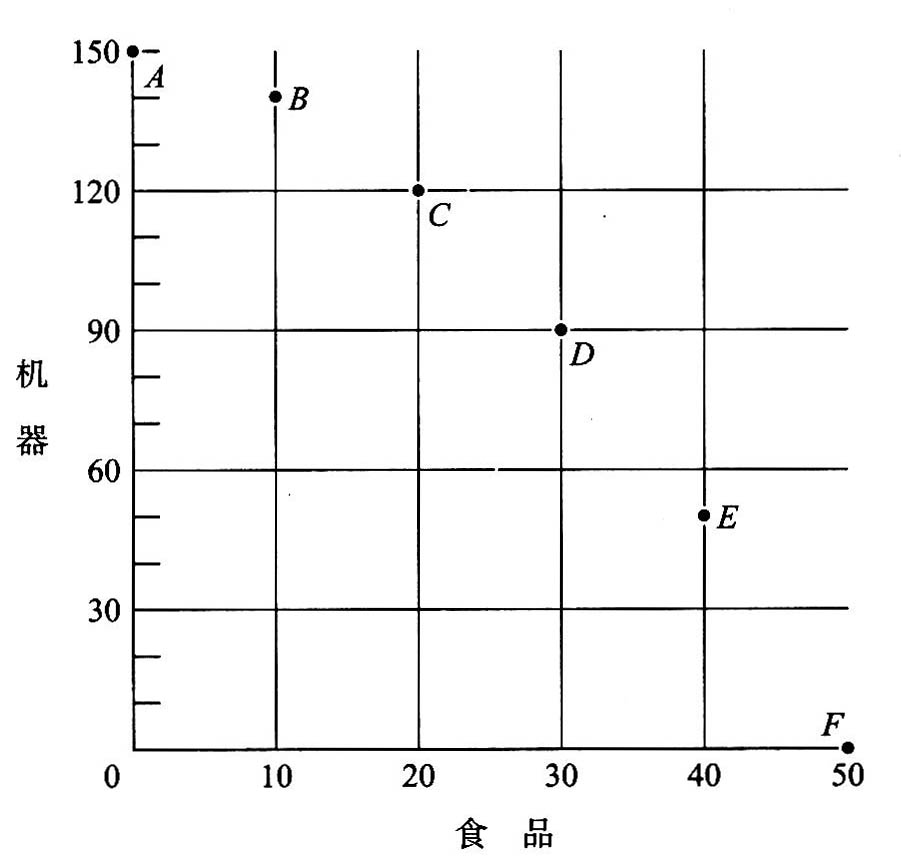
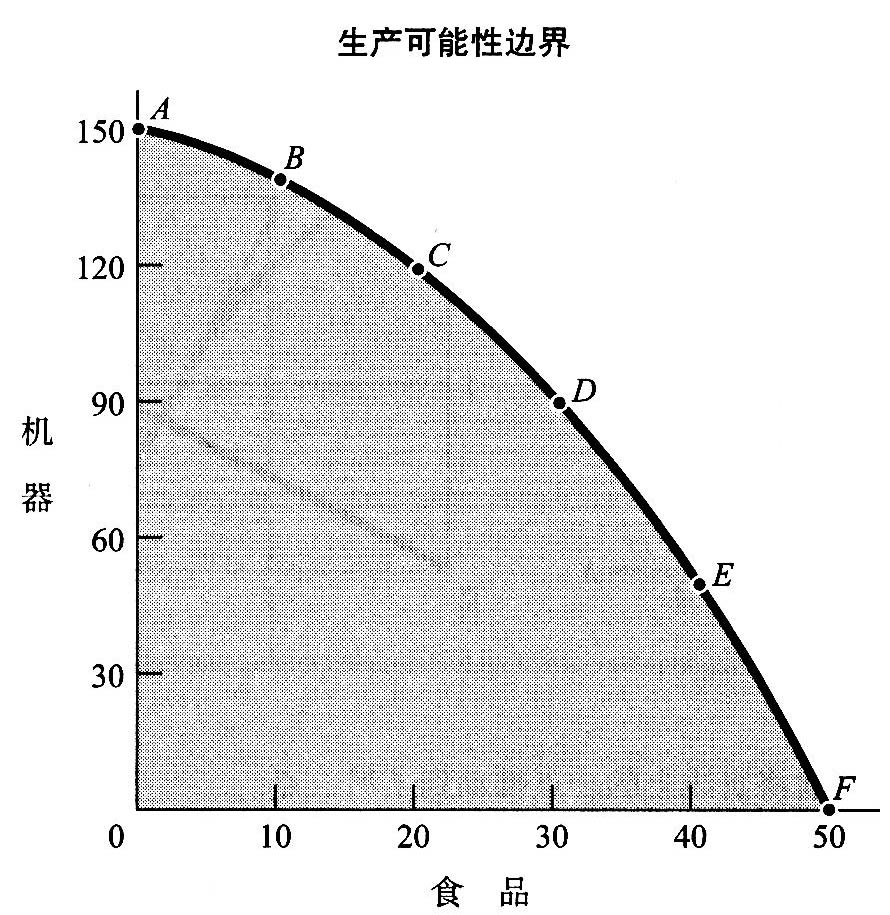
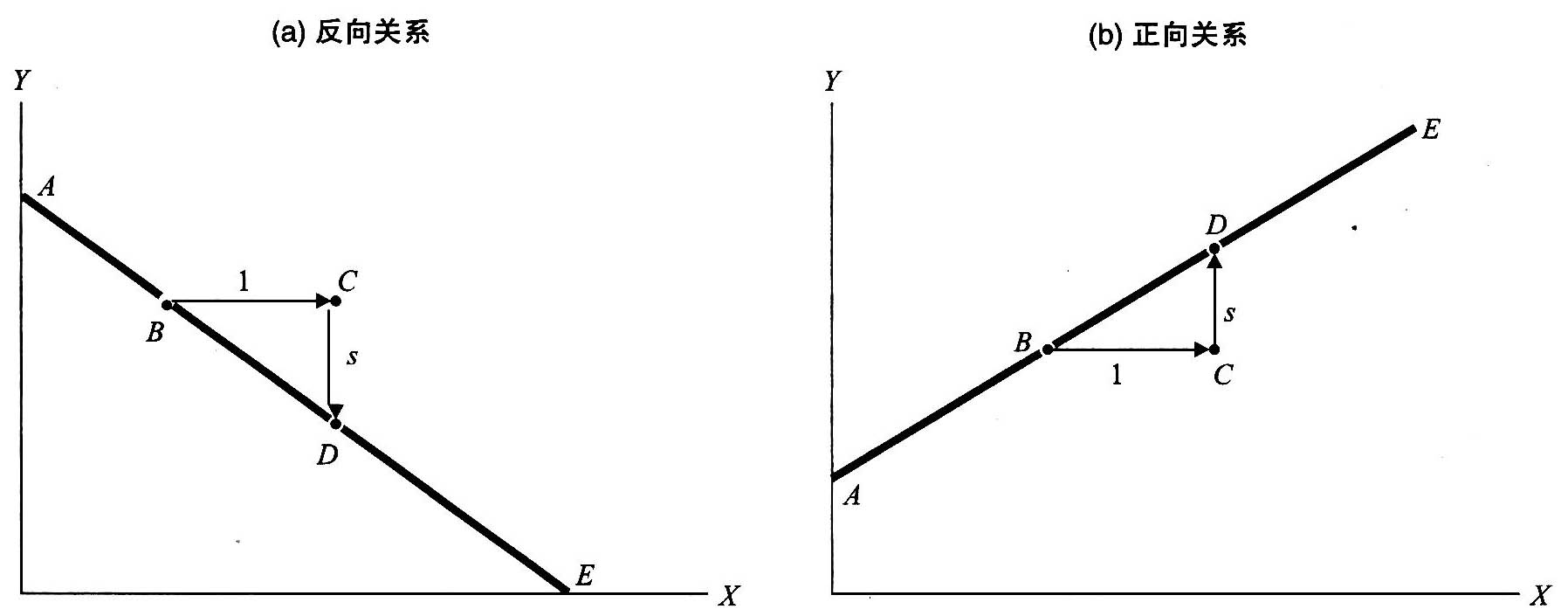
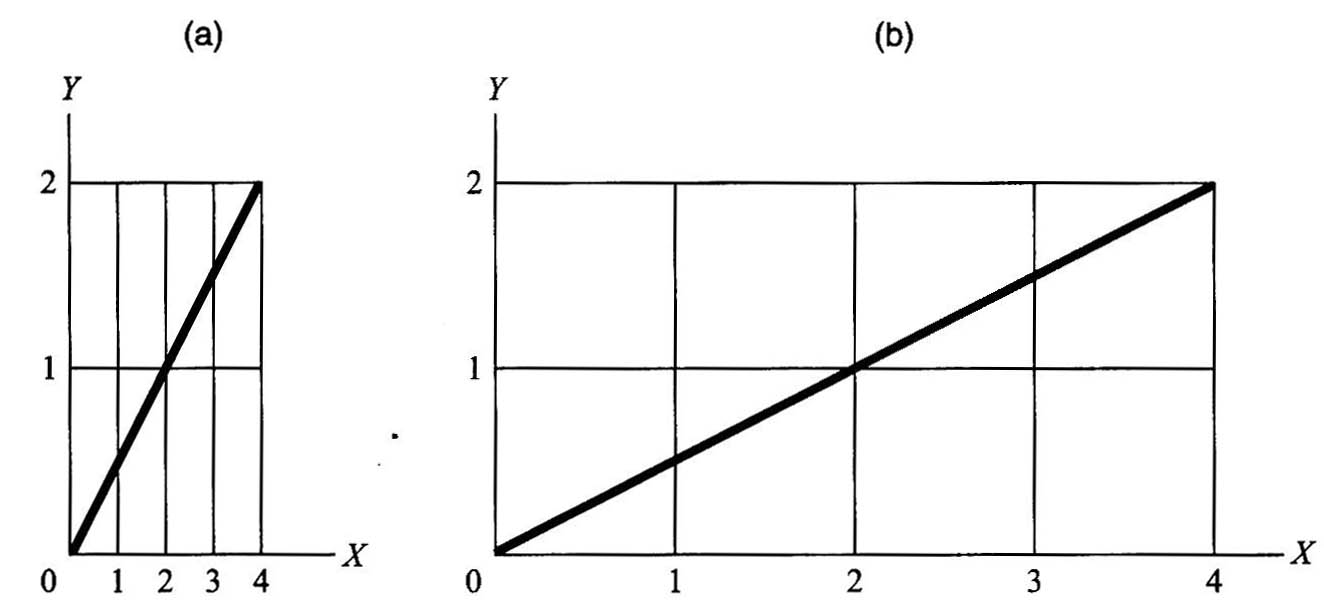
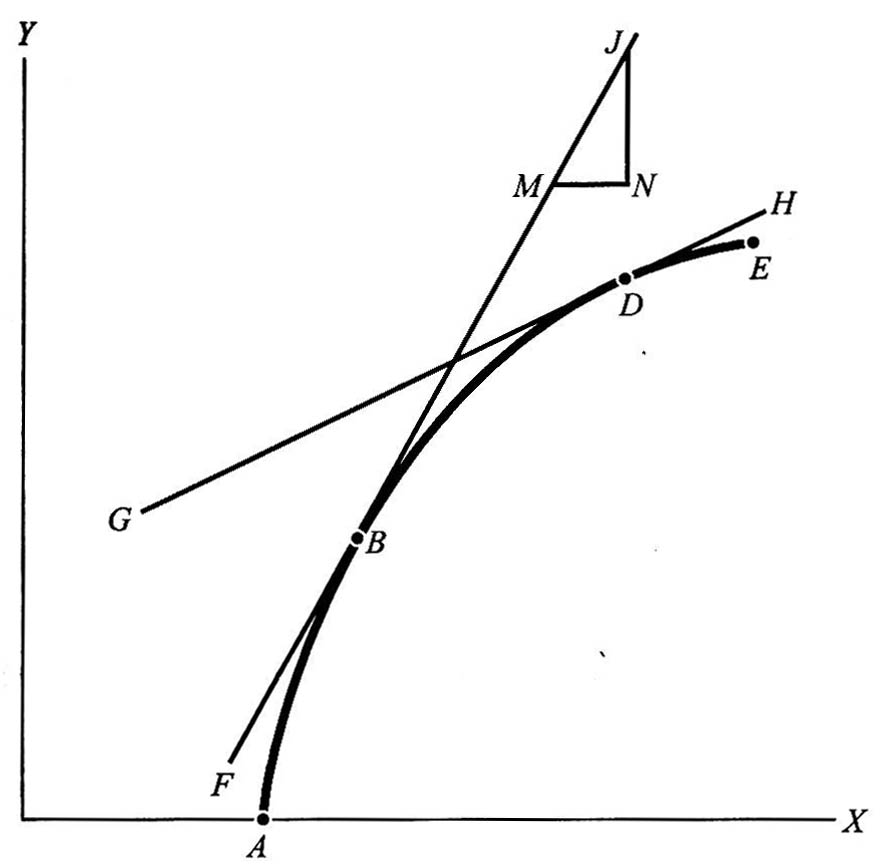
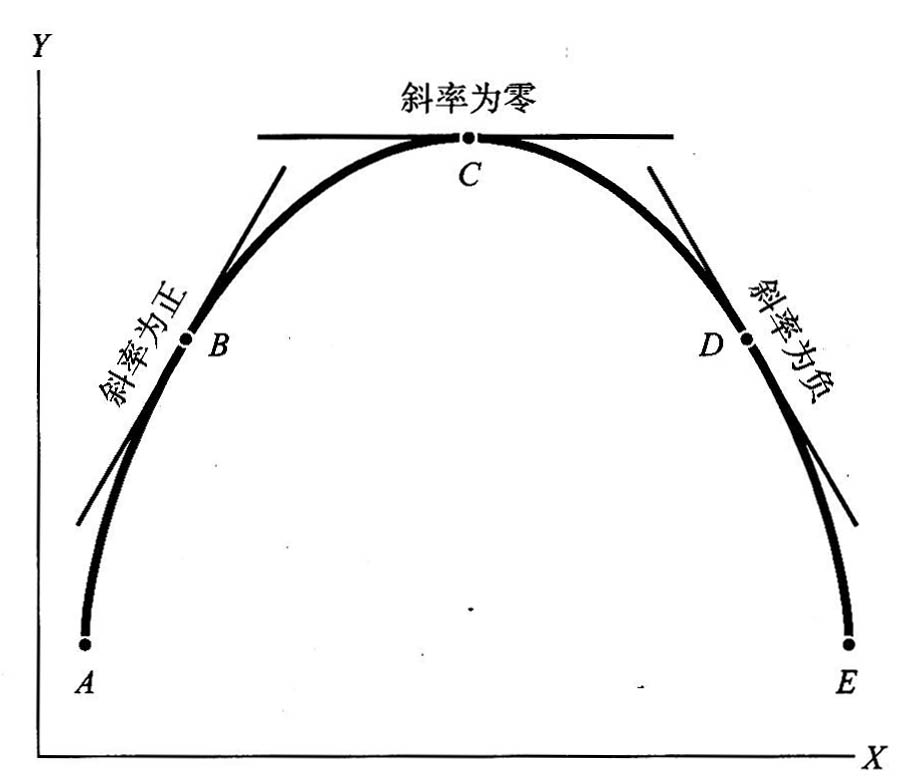
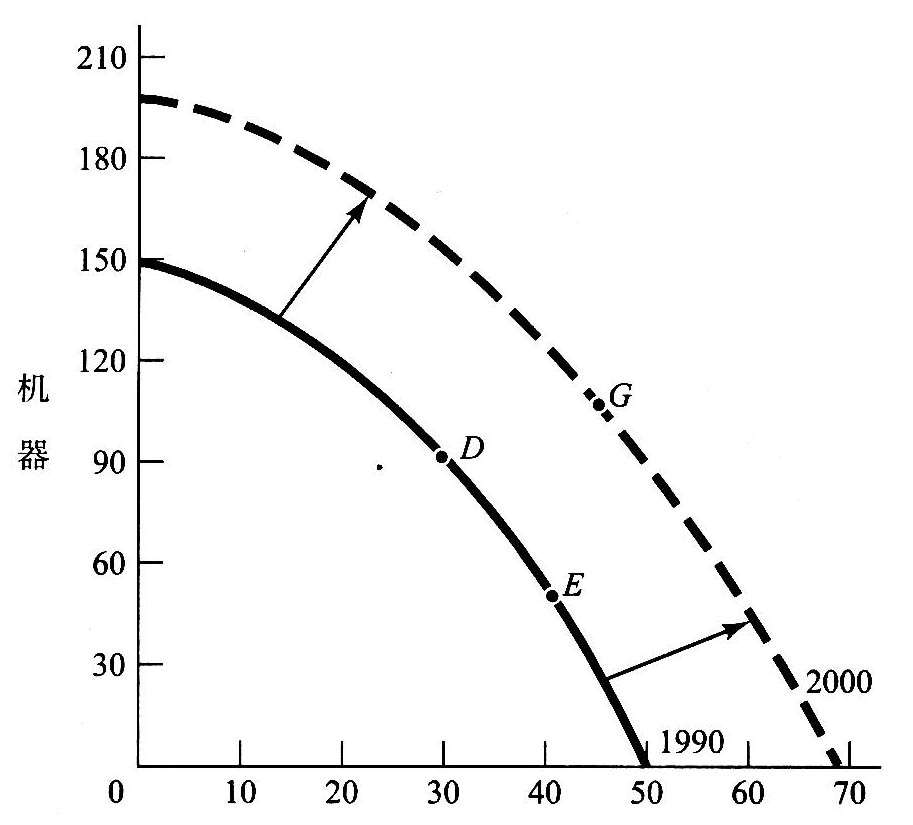
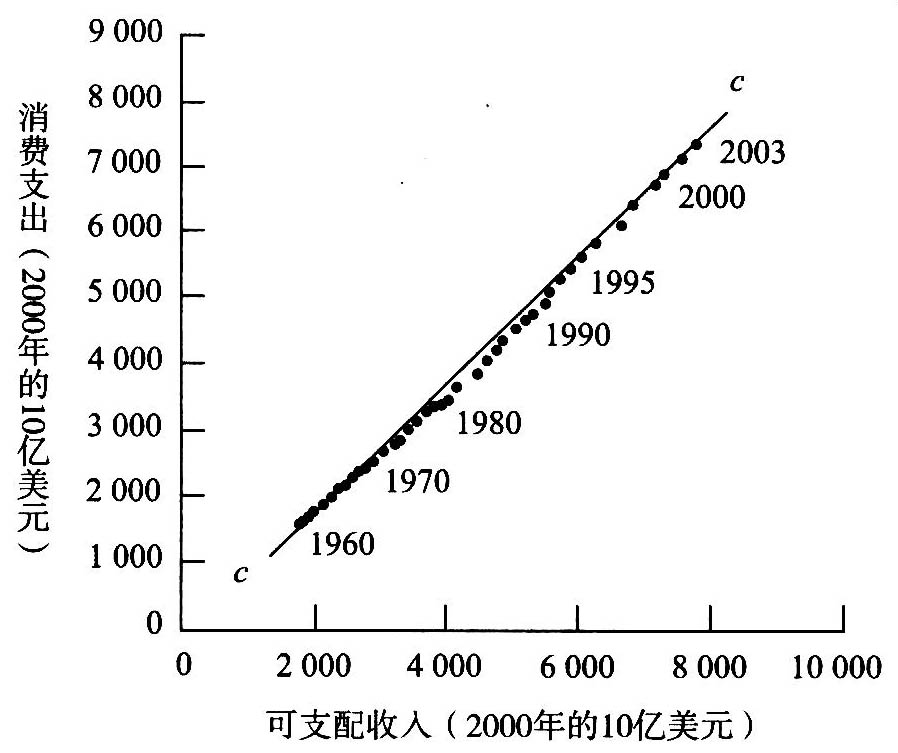
1.7.2第1章附录 如何看图
-
1.7.3第2章 现代经济中的市场与政府
-
1.7.4第3章 供给与需求的基本原理
-
1.8第二编 微观经济学:供给、需求和产品市场
-
1.8.1第4章 供给和需求的应用
-
1.8.2第5章 需求和消费者行动
-
1.8.3第5章附录 消费均衡的几何分析
-
1.8.4第6章 生产和企业组织
-
1.8.5第7章 成本分析
-
1.8.6第7章附录 生产、成本理论和企业决策
-
1.8.7第8章 完全竞争市场分析
-
1.8.8第9章 不完全竞争及其极端形式——垄断
-
1.8.9第10章 寡头和垄断竞争
-
1.8.10第11章 不确定性和博弈论
-
1.9第三编 要素市场:劳动、土地和资本
-
1.9.1第12章 市场如何决定收入
-
1.9.2第13章 劳动市场
-
1.9.3第14章 土地和资本
-
1.9.4第14章附录 市场和经济效益
-
1.10第四编 应用微观经济学:国际贸易、政府和环境
-
1.10.1第15章 比较优势和贸易保护主义
-
1.10.2第16章 政府税收和支出
-
1.10.3第17章 促进市场更富效率
-
1.10.4第18章 环境保护
-
1.10.5第19章 效率与公平:重大权衡
-
1.10.6第五编 宏观经济学:经济增长与商业周期
-
1.10.7第20章 宏观经济学概述
-
1.10.8第20章附录 宏观经济数据
-
1.10.9第21章 经济活动的均衡
-
1.10.10第22章 消费与投资
-
1.10.11第23章 商业周期波动和总需求理论
-
1.10.12第24章 乘数模型
-
1.10.13第25章 经融市场和货币的特殊形态
-
1.10.14第26章 中央银行与货币政策
-
1.11第六编 经济发展、经济增长与全球经济
-
1.11.1第27章 经济增长的进程
-
1.11.2第28章 经济发展的挑战
-
1.11.3第29章 汇率与国际经融体系
-
1.11.4第30章 开放经济的宏观经济学
-
1.12第七编 失业、通货膨胀与经济政策
-
1.12.1第31章 失业与总供给的基础
-
1.12.2第32章 保持价格稳定
-
1.12.3第33章 宏观经济学流派及其论战
-
1.12.4第34章 经济增长与经济稳定的政策
-
1.13专业术语表
-
1.14索引
-
1.15译后记
-
1.16版权信息
1
经济学