我们赖以生存的经济社会

之所以会存在突出的问题，

一方面是由于不能提供

充分就业，另一方面则是

因为武断而又不公平的财富

和收入的分配。

——凯恩斯

《就业、利息与货币通论》

（1936年）

美国和其他以市场为导向的经济社会一样，在产出、价格以及失业方面都面临着频繁而又无法预测的波动。过去这种波动被称为商业周期的波动，往往被认为是由于投资、消费、耐用品或国防方面的支出的波动所导致的。作为经济学者，我们有必要揭示和了解在支出的变动和产量就业的变动之间，存有什么样的传导机制？本章我们将介绍一种最简单的方法来理解商业周期，这个方法就是凯恩斯的乘数模型。

我们将在本章的第一部分中看到，在投资方面的支出增加是如何提髙消费者收人的，从而导致一种在未来支出上的逐渐递减但又总体放大的连锁反应。投资的变动由此可以视为一种对于产出的乘数化增长。在本章第二部分我们将会看到这种乘数机制其实可以应用到投资以外的领域中去。事实上，政府的采购、出口或其他外生的支出流的变化，都会被放大并加入到一个更大的产出变动中去。下面我们就来说明政府采购怎样像投资一样对产出产生乘数效应的。正是这一点使得许多宏观经济学家主张将财政政策作为稳定经济的工具。

乘数模型是第一个发展出来的完整的短期产出决定模型。但是它对经济的描述却过于简单化，这主要是由于它忽略了金融市场、货币政策，与世界的互动，以及价格和工资等重要的因素。这些因素我们将在以后必要的时候给予详尽的解释。现在我们将重点讨论：在决定国民产出的变动时投资和政府支出等因素的主导作用。

A.基本乘数模型

当经济学家们试图理解为什么战时大量军事开支会导致GDP的快速增长；为什么20世纪60年*（或80年代的减税曾经引发了一场时间较长的经济扩张；或为什么90年代末的投资繁荣会带来美国历史上时间最长的经济扩张的时候，常常可以在乘数模塾中找到最简明的解释。

究竟什么是乘数模型（multiplier model）?它是一个用来解释短期产出水平如何被决定的宏观经济学的理论范畴。“乘数”名称来自这样一个发现，即某些支出（如投资）的1美元变动会引起GDP的1美元以上的（或多倍的）变动。乘数模型能说明在一个存在资源闲置的经济中，对于投资、外贸、政府税收和开支政策等各种冲击会怎样影响产出和就业水平。乘数模型是建立在一个关键的假设上，即工资和价格都是固定的，同时社会资源是未被充分利用的。此外，我们还要暂时忽略货币政策的作用和金融市场对经济变化的反应。

储蓄与投资对产出的决定作用

不妨就一个高度简化的经济为例，先讨论为什么投资和储蓄在乘数模型中的作用是等价的。请回忆一下第22章中社会的消费函数和储蓄函数的图形。图24-1重现了这个图形。[ 1 ] 消费曲线上的每一点表示的是：在某个可支配收人水平上社会所意愿或计划的消费量。储蓄曲线上每一点所表示的是：在某个收人水平上社会所意愿或计划的储蓄量。这两条曲线密切相关，由于C+S永远等于可支配收人，所以消费曲线和储蓄曲线是一对镜像，它们加起来总是等于45°线。我们还可以将SS转制成图24-2。

我们知道，储蓄和投资取决于完全不同的因素：储蓄主要取决于可支配收人，而投资则取决于产出、利率、税收政策和企业信心。为了简化起见，我们将投资视为一种外生变量，即它的规模由模型以外的因素决定。

例如，有这样一个投资机会，即不论GDP水平如何，每年的投资均为2000亿美元。这就意味着，如果我们要画一条与GDP相对应的投资曲线，那么它必然是一条水平线。图24-2给出了这个外生性投资的例子。投资曲线标为II，以便与储蓄曲线SS区别（注意II，不是罗马数字的2）。

图24-2中储蓄曲线与投资曲线相交于E点。E点对应的GDP为M，代表了乘数模型中产出的均衡水平。

储蓄曲线和投资曲线的这个交点是国民产出在达到均衡时的GDP水平。

均衡含义的提醒

分析商业周期或者经济增长。的时候我们经常会考虑宏观经济“均衡”。这个术语到底是什么意思鬼？均衡（equilibrium）。就是不同的力在做功时达到平衡的一种状态。例如，如果你看到一个球正在滚下山坡，那么这个球就不是处在一种均衡的状态中，因为在这个过程中存有一个力在推动球向山下滚动，因此可以称之为非均衡（disequilibrium）。而当这个球滚到山下的某一洞中静止下来的时候，作用在球上的若干力就达到了平衡，那么这个球也就达到了均衡”。

简单地说，在宏观经济中，一个均衡水平的产出就是当支出和储蓄中的各种力达到了平衡，在均衡状态下，产出的水平总是趋向稳定，直到当支出与储蓄中的力有所改变，均衡才会被打破。

现在来看图24-2，其中E点是一种均衡。为什么我们说图24-2中的E点是一种均衡呢？原因在于在这个产出水平下，储蓄、投资和产出水平只有在E点，居民的意愿储蓄才能等于厂商的意愿投资。而只要意愿储蓄与意愿投资还不相等，产出就会进一步地上下调整。

图24-2中的储蓄曲线和投资曲线表示的是意愿的（或计划的）水平。这样，在产出水平为M时，所有企业想要投资的数量等于垂直距离ME。同样，在这一收人水平下，居民意愿储蓄的数量也为ME。但是，并不存在实际储蓄等于计划储蓄（或实际投资等于计划投资）的逻辑必然性。人难免会出错，或可能对将来预测不准。当发生这些错误时，实际的储蓄或投资数量就会偏离计划的水平。

为了解产出怎样调整到同意愿的储蓄量和投资量相对应的水平，我们这里考虑三种情况。第一种：经济处于E点。在该点，企业意愿投资曲线与居民意愿储蓄曲线相交。当每个人的计划都得到满足时，所有的人都将满足于继续以过去的方式去进行活动。

在均衡状态下，企业不会再有存货堆积，也不再会感到销售特别兴旺而不得不提高产量。因此，产出、就业、收人及支出都将保持不变。在这样的情况下，GDP会停留于S点，因而我们可以恰当地将该点称为一种均衡。

第二种情况是GDP—开始高于E点。比如说在4点，GDP处于M点的右方，处于储蓄曲线高于投资曲线的某个收人水平。这不是一种均衡，因为在该收人水平上，居民储蓄量多于企业意愿进行的投资。因此，企业将会找不到足够的顾客，从而使商品存货多于企业的理想水平。在这种情况下企业怎么办呢？它们会减少产量并解雇工人。这就会使GDP逐渐下降，在图24-2中表现为产出向左移动。只有到E点，经济才能回到均衡状态。而且在该点，继续变动的倾向也就会消失。

论述到此，你应能自己分析第三种情况。如果GDP低于其均衡水平，强大的力量会使它向右移动，直至回到E点。

上述三种情况可得出同一结论：

GDP惟一的均衡水平是处于计划的储蓄与投资相等的E点。在其他的任何产出水平上，居民意愿储蓄的数量都不等于企业意愿投资的数量。这种不一致会导致企业改变其产量和就业水平，从而使经济体系回复到均衡的GDP水平。

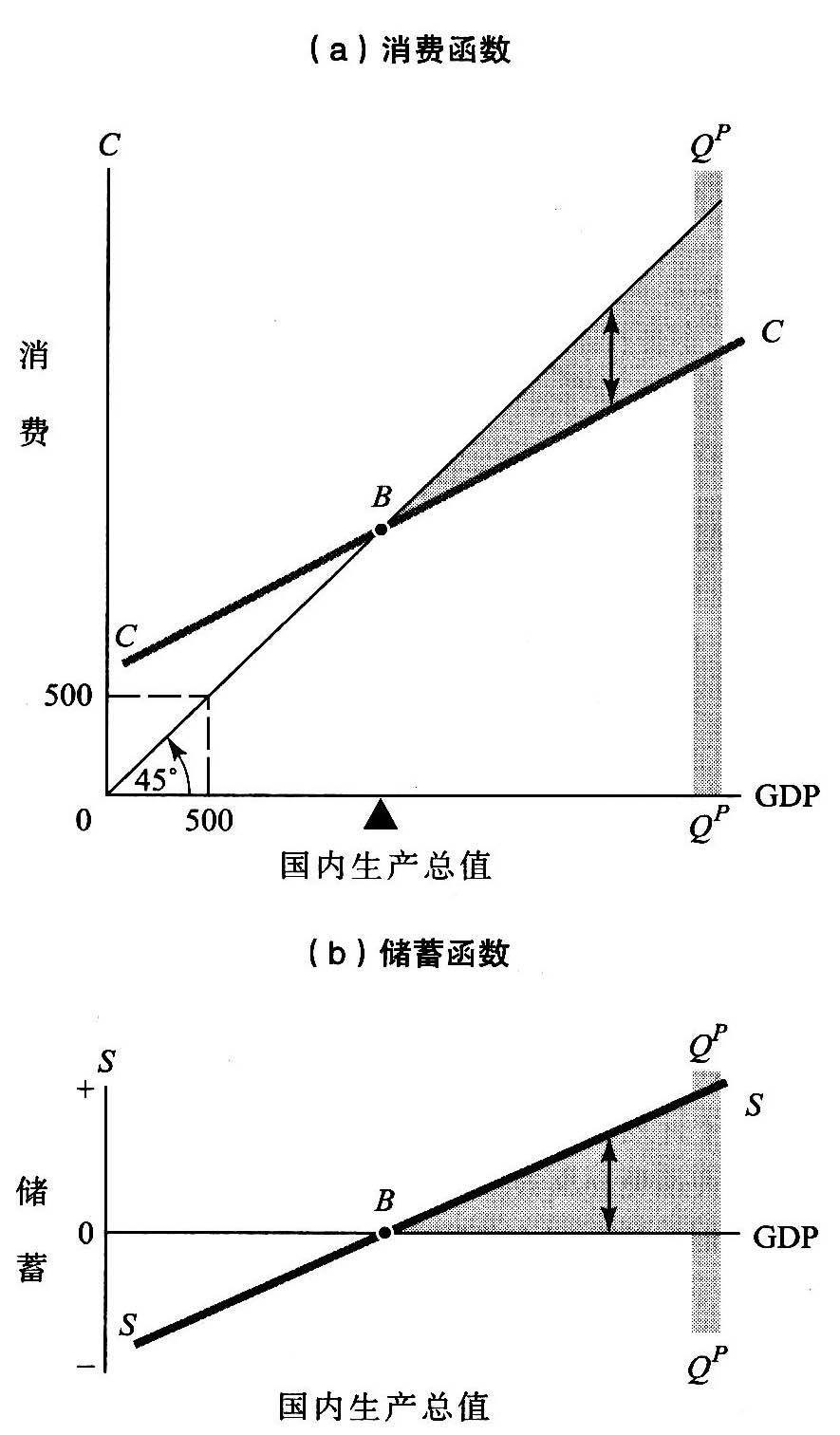
图24-1  国民产出决定消费和储蓄的水平

回忆第22章中的消费函数和储蓄函数，CC和SS，它们是一对镜像曲线。上面图中的收支均衡点位于B，它对应着下面图形中的零储蓄点，即SS曲线与横轴的交点。(a)图中标有“500”的点强调了45°线的重要性质：在该线上的任意一点到纵横两轴的距离都刚好相等。标着#的阴影部分所表示的是潜在的GDP水平。

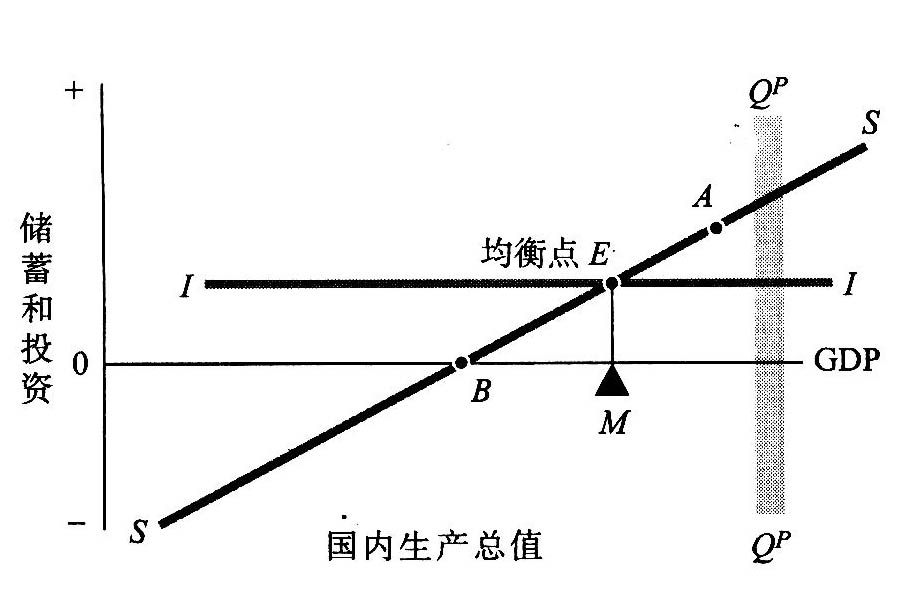
图24-2  国民产出的均衡水平由储蓄和投资曲线的交点决定

水平的//线说明投资数量保持不变。E是投资曲线与储蓄曲线的交点。均衡GDP位于SS曲线和II曲线的交点，因为只有在这一GDP水平上，居民意愿储蓄的数量才正好等于企业意愿投资的数量。

总支出对产出的决定

第二种方法是用总支出法来决定一国家的产出，对于学生可能更直观。图24-3描述了这一方法。它显示了相应于总产出或总收人的一条总支出曲线。CC曲线代表的是消费函数，它体现与每一个收入水平相对应的意愿的消费数量。然后，我们将意愿投资（即固定的数量I）加到消费函数上，这样意愿的支出总量，或者称为TE，就为C+，如图24-3中上面的C+I曲线所示。

接下来我们画一条45°线，以帮助我们确定均衡。在45°线上的任何一点，总意愿支出（以纵轴衡量）都正好等于产出总量（用横轴衡量）。

现在我们很容易地就能计算出图24-3中的均衡产出水平。只有在意愿的支出总量（由叹曲线代表）等于总产出量的那一点上，经济才处于均衡状态。

总支出（或TE）曲线表示对应于每一个产量水平，消费者和企业意愿支出的数量。在图24-3中TE=C+I曲线与45°线的相交E点，经济处于均衡状态。这是因为，在这一点上，对消费和投资的意愿支出数量正好等于总产出量。

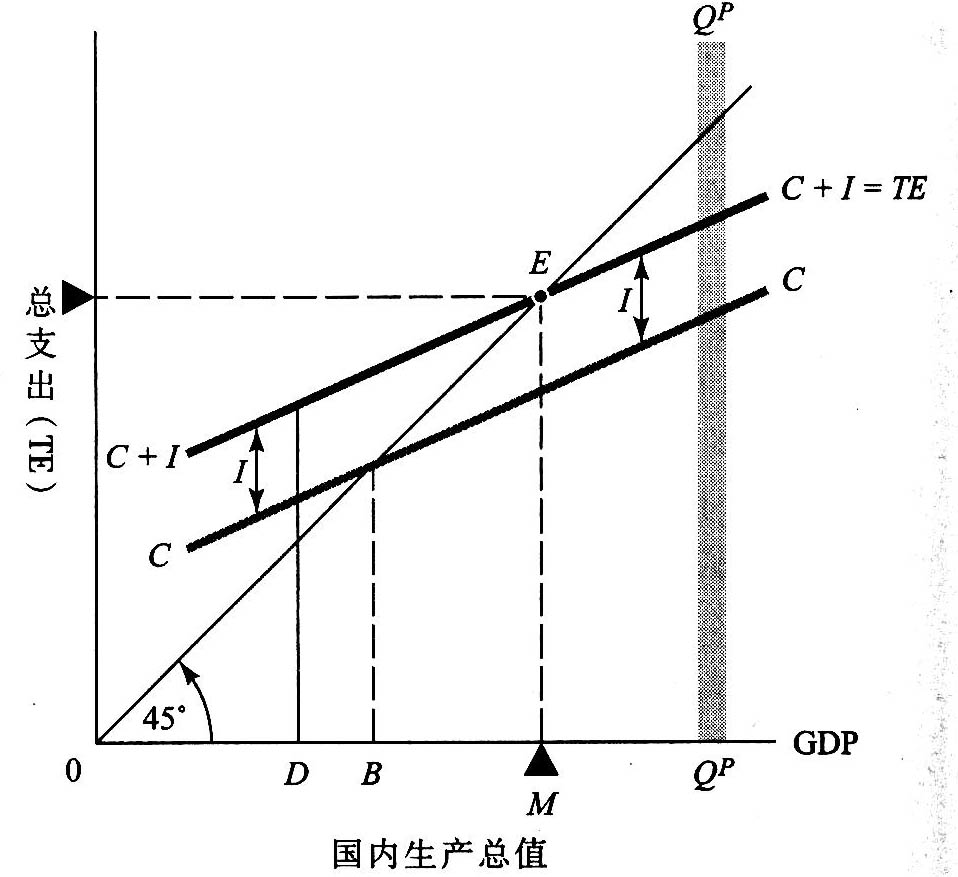
图24-3  按照总支出法，均衡GDP水平还可以用C+I=TE曲线与45°线的交点表示

把II加到CC,就可以得到总意愿支出曲线C+I。在E点，即C+I曲线与45°线的交点，我们得到了与储蓄一投资所示的相同的均衡水平。(注意本图与图24-2的相似之处：加到CC曲线上的投资和图24-2的是相同的；交点E：也必然处于相同的位置。)

调节机制

我们可以先来分析为什么E点是一个均衡水平。一个均衡的经济就意味着计划的（C和）支出量等于计划产出量。如果经济偏离均衡状态，比如说在图24-3中产出水平处于Z）点，那么将会怎样呢？在这一产出水平，支出线C+处于45°线上方，因而计划的C+J将大于计划的产出量。这意味着消费者愿意购买的货物的数量大于企业生产的数量。这时汽车销售商将会发现他们的存货逐渐消失，电脑厂商向分销商配货的周期也会越来越长。

在这种非均衡状态，汽车经销商和电脑经销商将会增加它们的订货。汽车厂将会重新雇佣被解雇的工人并加快生产线运转，电脑厂商也会加快组装和配送。这样，总计划产出与总计划支出之间的差异就导致产出数量的变动。

由此可以推知，只有当厂商生产的数量等于居民和厂商计划开支的C加时，即在E点，经济才能达到均衡。（你应该也可以推知，当产出高于均衡水平时将会发生什么情况。）

计划数置与实际数置

本章，我们一再提到“计划好”或者是“意愿的”支出和产出9这些词提醒人们注意以下两者的区别：（1）计划的或意愿的消费或投资的数量是由消费函数或投资需求曲线所决定的；（2）实际的消费和投资数量是事后衡量的。

下面的对话可能有助于你记住这种区别：

糊涂者：我记得你说过储蓄永远等于投资。

清醒者：很正确。正如国民核算的统计人员所衡量到的那样，不论是繁荣还是衰退的时期，储蓄和投资都总是正好相等。

糊涂者：要是储蓄永远等于投资的话，那我为什么还必须区分计划的和意愿的？

清醒者i这是由于只有当厂商和消费者都处于他们的意愿的支出曲线和投资曲线上时，GDP才有可能达到均衡水平。

糊涂者：当计划的和实际的有差别时又会怎样呢？清醒者：事实上，实际投资经常会与计划投资不同。例如，通用汽车也许会无法完成它的销售计划。这时它就会发现它的存货增加。这种在存货投资上的非自愿性增加就不是一个均衡，。那么通用汽车将不可避。免地削减生产。

糊涂者：啊哈！我明白了，只有当产出水平处于计划支出（C+I）等于计划产出的时候，产出、收入或支出才不存在继续变动的趋势。清醒者。完全正确。

数据分析

举个数据例子也许有助于说明为什么在计划支出等于计划产出量时，产出会达到均衡。

表24-1给出了关于消费函数和储蓄函数的一个简单的数据例子。收支相抵的收人水平（国家非常穷以至于在资产负债表上没有净储蓄）假设为3万亿美元。假设收人每变动3000亿美元会导致储蓄变动1000亿美元和消费变动2000亿美元。换句话说，为了使问题简单化，假设边际消费倾向MPC为一个常数，其数值为23，则边际储蓄倾向MPS为13。

假设投资是外生的，投资规模将总是2000亿美元，如表24-1第（4）栏所示。这就是说，不论GDP如何变动，企业所意愿购买的投资品都将是2000亿美元，不会多也不会少。

第（5）栏和第（6）栏是关键。第（5）栏显示的是GDP总量，不过是将第（1）栏简单地复制到第（5）栏。第6）栏表示厂商每年的实际可销售量，等于计划消费量与计划投资量之和，实际上即为数字表示的图24-3中的C+I曲线。

当所有企业作为一个整体，生产的总产品过多（多于消费者和企业想要购买的数量之和）时，企业就会非自愿地积压商品存货。

从表24-1的第一行可见，如果企业临时生产的GDP为4.2万亿美元，而计划的或意愿的支出数量[第（6）栏1只有4万亿美元，在这种情况下，则过多的存货就会累积起来。企业将减缩产量，GDP就会下降。表24-1中最下边一行所表示的情况相反，总支出数量为3万亿美元，而产出数量为2.7万亿美元。于是存货会逐渐耗尽，企业会扩大生产从而增加总产出。

我们还可以看见，一旦其生产量大于它们能够以有利的价格销售的数量时，作为一个整体的厂商就会减缩作业量，从而GDP趋于下降。当销售的数量大于目前产量时，它们就会增加产量，GDP就会上升。

只有当第（5）栏的产出水平正好等于第（6）栏的计划支出量（7五）时，经济才会处于均衡状态。只有在均衡状态时，它们的销售量正好继续维持总产出的现有水平。GDP既不扩大也不缩小。

表24-1  用算术方法，可将均衡产出视为计划支出置等于GDP的水平

表中灰度较深的一行表示均衡的GDP水平。在这个水平上，正在被生产出来的3.6万亿美元正好等于居民计划消费和厂商计划投资的总和。在该行以上的两行，企业将被迫进行非意愿的存货投资，并将缩减产量，直至于达到均衡的GDP。请你解释在该行以下各行趋于均衡GDP的扩张趋势。

乘数

乘数究竟在哪里呢？为回答这一问题，我们需要考查外生的投资变化如何影响GDP。投资的增加会提高产出和就业水平，这在逻辑上是必然的。但是会提高多少呢?乘数模型说明，投资的增加将会引起更大的乃至数倍的GDP的增加，也即投资所引起的GDP的增加量会大于投资本身的增加量。

乘数（multiplier）是指外生支出变化1美元对于总产出的影响。在简单的C+I模型中，乘数是投资变化率和总产出变化率的比率。

请注意，乘数的定义是指每单位外生支出的变动所导致的总产出的变动。这表明支出的某些组成部分是在模型外给定的。在上面提到的例子中，外生的变量是投资。稍后我们会看到同样的方法也可被用于讨论政府支出、出口以及其他总产出项目等变量对于总产出的效应。

例如，假设投资增加1000亿美元，如果这个增加导致产出增加3000亿美元，则乘数就是3。而若所引起的产出增量为4000亿美元，则乘数就为4。木屋和木匠乘数为什么大于1?假设我利用闲置资源建造了一幢价值1000美元的木屋。我的木匠和木材生产者会因此增加1000美元的收人。但事情并未到此为止。如果他们的边际消费倾向（MPC）均为23，则他们会支出666.67美元购买新的消费品。因而这些商品的生产者又会增加666.67美元。如果他们的MPC也是23，则他们又会支出444.44美元，或者说是666.67美元的23（或是1000美元的23的23）。这个过程会一直继续下去，每一轮新支出都是上一轮收人的23。

这样，我最初的1000美元的投资就导致了一系列次一轮的再消费支出。尽管这一系列的再支出永无止境，但其数值却是一次比一次减少。最终的总和是一个有限的量。

应用简单算术，我们可计算出总的支出增量：

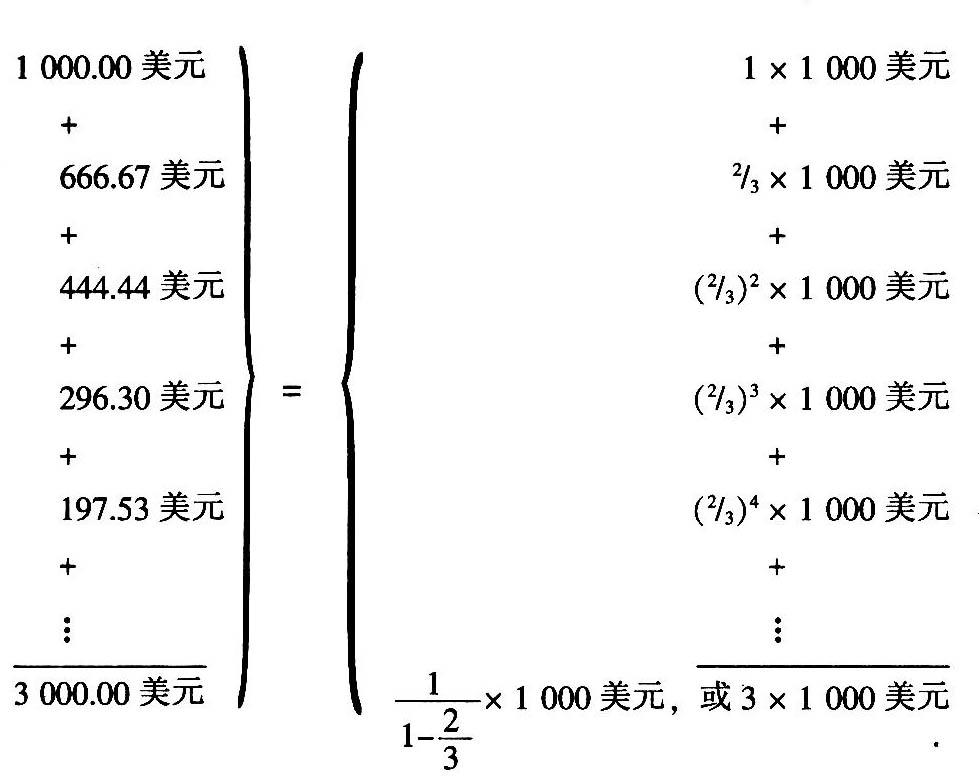
这就说明，如果MPC等于23，则乘数为3；它包括最初的投资（倍数）1和所引发的一系列次轮消费（倍数）2。

如果MPC是3/4，相同的演算会得出乘数是4，因为，1+3/4+（3/4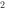）+（3/4）+…的总和为4。如果一个说是1/2的MPC的话，则乘数为2。[ 2 ]

因此，乘数的大小取决于MPC的大小。或者，我们也可以用MPC的相关概念，即边际储蓄倾向如果MPS等于1/4，则MPC为3/4，而乘数为4。如果MPS为1/3，则乘数为3。如果MPS为1/x，则乘数为x。

现在可以明确地看到，简单的乘数总是边际储蓄倾向的“倒数”，因此，等于1/（1-MPC）。简单的乘数公式是：

产出的变动=1/MPSx投资的变动

                              =1/（1-MPC）x投资的变动

乘数的图形

迄今为止，我们的乘数讨论很大程度上还依赖于常识和数学计算。能否通过分析储蓄和投资的图形而得出相同结果呢？答案是肯定的。

假设，如表24-1中，MPS为1/3，并假设因发明涌现而增加了1000亿美元的投资。那么新的均衡GDP水平应该是多少呢？如果乘数定为3，则GDP应该增到39000亿美元。

图24-4可证实这一结果。我们原有的投资曲线向上移动了1000亿美元，达到了新的水平I'I'。新的交点为E'；收人的增加正好是投资增加的3倍。正如图中箭头所示，横轴上代表产量增加的距离是投资曲线向上移动距离的3倍。我们知道，意愿的储蓄数量必然会上升到与新的更高的投资水平相等为止。储蓄增长的惟一途径是国民收人增加。如果MPS为1/3，投资增加额为1000亿美元，那么收人必然增加3000亿美元，才能拿出1000亿美元的储蓄来满足新的投资需要。这样，在均衡水平上，1000亿美元的投资增量才能引致3000亿美元的收入增量，从而证实了我们关于乘数的算术推导。[ 3 ]

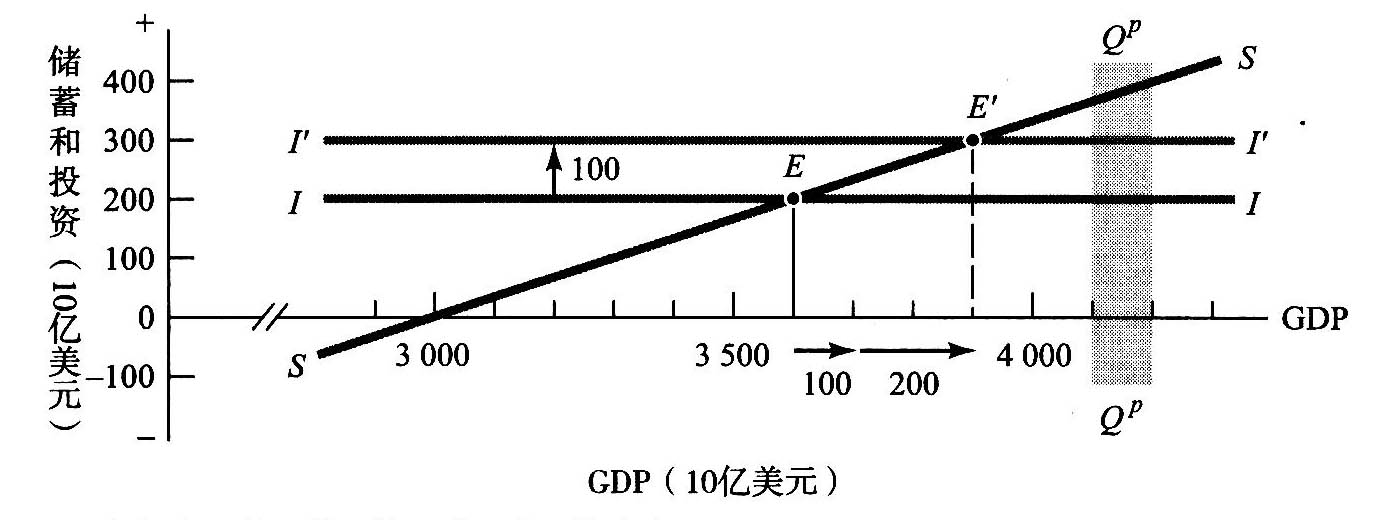
图24-4  每投资1美元能“倍”增3美元的产出

新投资把II向上移到I'I'。E'给出了新的均衡产出，其中投资每增加1，产出就会增加3。(注意：分为两段的水平箭头是投资移动的垂直箭头长度的3倍。之所以将水平的箭头分为两段，是表示每1美元的最初投资具有2美元的一系列次轮再消费支出。)

展望乘数模型

在过去的半个世纪中，最简单的乘数模型一直对于商业周期理论产生着巨大的影响。但是它给出的却是一个过于简单的经济图景。它所忽略的一个最重要的问题是金融市场和货币政策对经济的影响。产出的改变会影响利率，而利率又反过来影响经济。此外，最简单的乘数模型也忽略了国内经济和世界其也经济体的相互影响。最后，该模型还忽略了经济的供给方，经由与总供给相联系的支出与价格的相互作用而表示出来。所有这些缺点我们都会在以后的章节中予以补充，但我们一定要记住，这个人类发展出来的第一个宏观经济学模型，绝对是我们探索和理解经济社会那神奇的复杂性的一块不可或缺的基石。

不妨将以上所论综合起来讨论乘数模型如何更普遍地被应用于宏观经济分析。这种讨论将会很有助益。我们试着理解是什么因素在决定一国的国民产出水平。从长期看，一国的产出水平和生活标准是由它的潜在生产能力来决定的。但在短期内，商业环境使得经济高于或低于其长期趋势。而产出和就业对于各自趋势的偏离可以由简单的乘数模型或者是与其相似但却更为复杂和全面的模型来解释。

尽管这里所展示的种种关系都是被简化了的，但其主旨还是有效的，甚至在扩展到包括政府财政政策、货币政策和对外贸易等情况的时候，其原则也依然适用。需要提请注意的一点是：乘数分析只适用于有闲置资源存在的情况。只有在存在过剩的生产能力的条件下总需求的增长才可能引起产出的增长。相反，如果一种经济正处于其潜在的产出水平，那么就没有产出随着总需求扩张而扩张的空间。在充分就业条件下，需求的增长不会引致的产出增加而只会引致价格的上升。

当经济中存在过剩的生产能力和失业人口时，增加投资或其他支出，所增加的这些支出最终会更多地导致实际产出的增长，而较少地会导致价格水平的上涨。然而，当经济达到并超过其潜在产出时，在现有价格水平上要想引出更多的产出就是不可能的。因此，在充分就业情况下，增加支出只会导致价格水平上升，而很少或完全不会引起实际产出或就业的增加。

乘数模型与AS-AD模型的比较

了解了乘数模型，你也许会自问，是否能用我们在第20章中所学到的AS-AD（总需求一总供给）模型来解释乘数模型呢？事实上，这不是两个不同的方法。乘数模型就是总需求一总供给模型的一个特例。它解释了在特定的精确假设下，AD是如何受消费和投资支出影响的。

乘数模型的核心假设是：在短期内价格和工资都是固定不变的。这个假设过于简单，因为在现实生活中价格是迅速变化的。但是该假设却捕捉到一个要点，即，如果某些工资和价格具有粘性一这是不争的事实，那么一些使得AD发生移动的变化就会导致产出的变化。在以后的章节中我们还会回到这一重要的命题上来。

图24-5说明了乘数分析与方法之间的关系。(b)图展现了一条完全竖直的曲线。当产出等于潜在产出时，曲线就会变成垂线。

而在潜在产出线的左侧，由于存在着闲置资源，产出主要由总需求大小决定。当投资增加时，会引起AD增力口，从而使均衡产出上升。

同样的经济过程也可以用图24-5上面的乘数图形来描述。乘数图形中的均衡给出了与均衡相同的产出水平，二者都得到了实际GDP的数量Q。它们只不过是强调了产出决定的不同侧面。

这一讨论还指出了乘数模型的一个非常重要的特点。对于描述萧条甚至衰退来说，它也许是个十分有用的方法。然M它却不能应用于充分就业时期。一旦当工厂正以其最大生产能力运作，同时所有的劳工都已经被雇佣时，那么，对于这样一种经济来说，就不可能再增加产出了。

对于简单乘数模型的说明我们不妨到此结束，接下去将会进一步拓展关于总需求的讨论，分析图形中将会增加政府财政政策等变量。

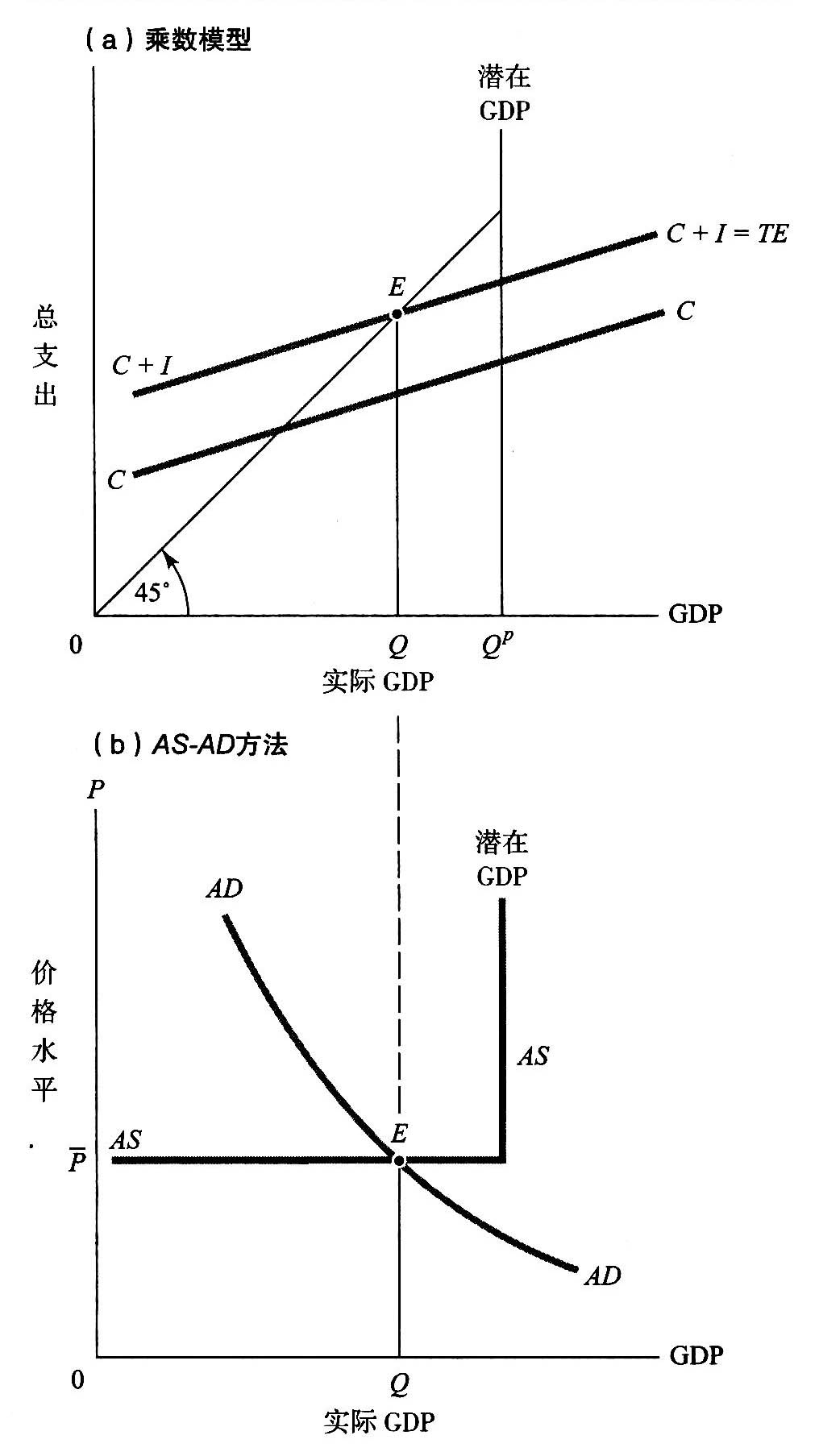
图24-5  乘数模型如何适用于AS-AD方法

乘数模型是一种理解均衡如何运作的方法。

(a)上图表示乘数模型中的产出一支出均衡。在E点，支出线正好与45°线相交，导致了均衡产出Q。

(b)这一均衡也可以在下图中看到，这时AD曲线与AS曲线相交于E点。在简单乘数模型中，假设工资和价格固定，所以AS曲线是水平的，直到达到充分就业为止。两种方法都引出了完全相同的均衡产出，即Q。

B.乘数模型中的财政政策

几个世纪以来，经济学家们已经认识到财政政策（政府的税收和支出计划）的分配作用。人们也早已知道，财政计划有助于决定国民产出应当如何在集体消费和私人消费之间分配，以及如何在人口中分担公共支出的负担。

随着现代宏观经济学理论的进一步发展，一个十分令人惊奇的事实已经被揭示出来：政府财政对产出、就业和价格的短期变动也有着重要的宏观的影响。财政政策对经济活动有重大影响，这一点促使了凯恩斯主义的宏观经济政策理论的出台。该理论认为：为缓和商业周期，政府行为具有积极的作用。这一点被著名的宏观经济学家诺贝尔经济学得主詹姆斯托宾阐述如下：

凯恩斯主义的政策，首先体现为宏观经济政策对实际经济目标所做出的显著贡献，尤其对实现充分就业和国民收入实际增长这样的目标；其次，凯恩斯主义者要求积极主动的管理；第三，凯恩斯主义者希望将财政政策和货币政策紧密结合起来，共同促进宏观经济目标的实现。

在这一部分，我们将用乘数模型说明政府采购如何影响产出。

财政政策怎样影响产出

为了理解政府在经济活动中的作用，我们需要考査政府的支出和税收，以及这些活动对私人部门支出所产生的影响。现在我们通过在C+I中加人G来修改前面的分析，从而可以得到一条新的总支出曲线TE=C+I+G。当政府及其支出和税收被考虑进来时，我们就可以在图形中用这条曲线来描绘宏观经济的均衡状态。

为了使问题简化，我们在分析政府采购的影响之前，先假设税收总量是固定不变的（这种不随着收人和其他经济变量变动的税收称为一次性总付税收）。但是，即使假定税收的货币价值不变，我们也不能再忽视可支配收入与国内生产总值的差别。在简化（不考虑外贸、转移支付或折旧）条件下，第21章曾告诉我们，GDP等于可支配收人加税收。进而，在假定税收保持不变时，GDP和可支配收入）之间永远相差一个相同的数量；这样，将税收考虑进来以后，我们仍能用CC曲线来对应GDP而不是DI。

图24-6显示的是：存在税收时消费函数是如何改变的。我们用黑色的CC线画出初始无税收的消费函数。此时，GDP等于可支配收入。我们使用和表24-1中一样的消费函数，所以，当GDP（和DI）为3000时，消费量也是3000，等等。

现在引人为数300的税收。在）为3000时，GDP必须等于3300=3000+300。当GDP为3300时，消费仍为3000，因为DI为3000。由此，可将消费曲线向右移到C'C'就能将消费写成GDP的函数；向右移动的数量正好等于税收的数量，即300。

同样，我们还可以将新的消费曲线画成向下移动了200的一条平行线。如图24-6所示，200是将收人的下降量300乘以边际消费倾向的数值2/3的结果。

现在再看总需求的构成，第21章曾告诉我们，GDP由4个部分组成：

GDP=消费支出

                         +国内私人总投资

                                        +政府对产品和服务的采购

           +净出口

          =C+I+G+X

现在假定经济是封闭的、不存在对外贸易，则GDP由前3项组成，即等于C+I+G。（等我们讨论开放条件下的宏观经济学时再将最后一项净出口加上。）

图24-7可显示政府采购的影响。这个图与本章前一部分中所用的图（见图24-3）几乎完全相同。在这里，我们在消费和投资量上加人了新的支出流G。如图所示，我们在消费曲线和固定投资量之上，又加人了一个新变量G（政府在商品和服务上的支出）。也就是说，曲线C+I与新曲线现TE=C+I+G之间的垂直距离就是G的数额。

为什么我们简单地将G加在消费和投资之上呢？因为政府建筑一座房子的支出（G）与私人建筑一座房子的支出（G）对宏观经济具有相同的影响；同样，包括购买政府办公用车的公共消费开支（G）与私人购买轿车的消费开支（C）对就业也具有相同的作用。

我们最后得到由二者叠加在一起的TE=C++G，可计算出，在每一GDP水平上将会出现的总支出量。现在，我们必须根据它与45°线的交点来找出GDP的均衡水平。在GDP的这个均衡水平，如图24-7中的E点，总的计划支出量正好等于总的计划产出量。因此，将政府采购加人了乘数模型后，E点就是产出量的均衡水平。

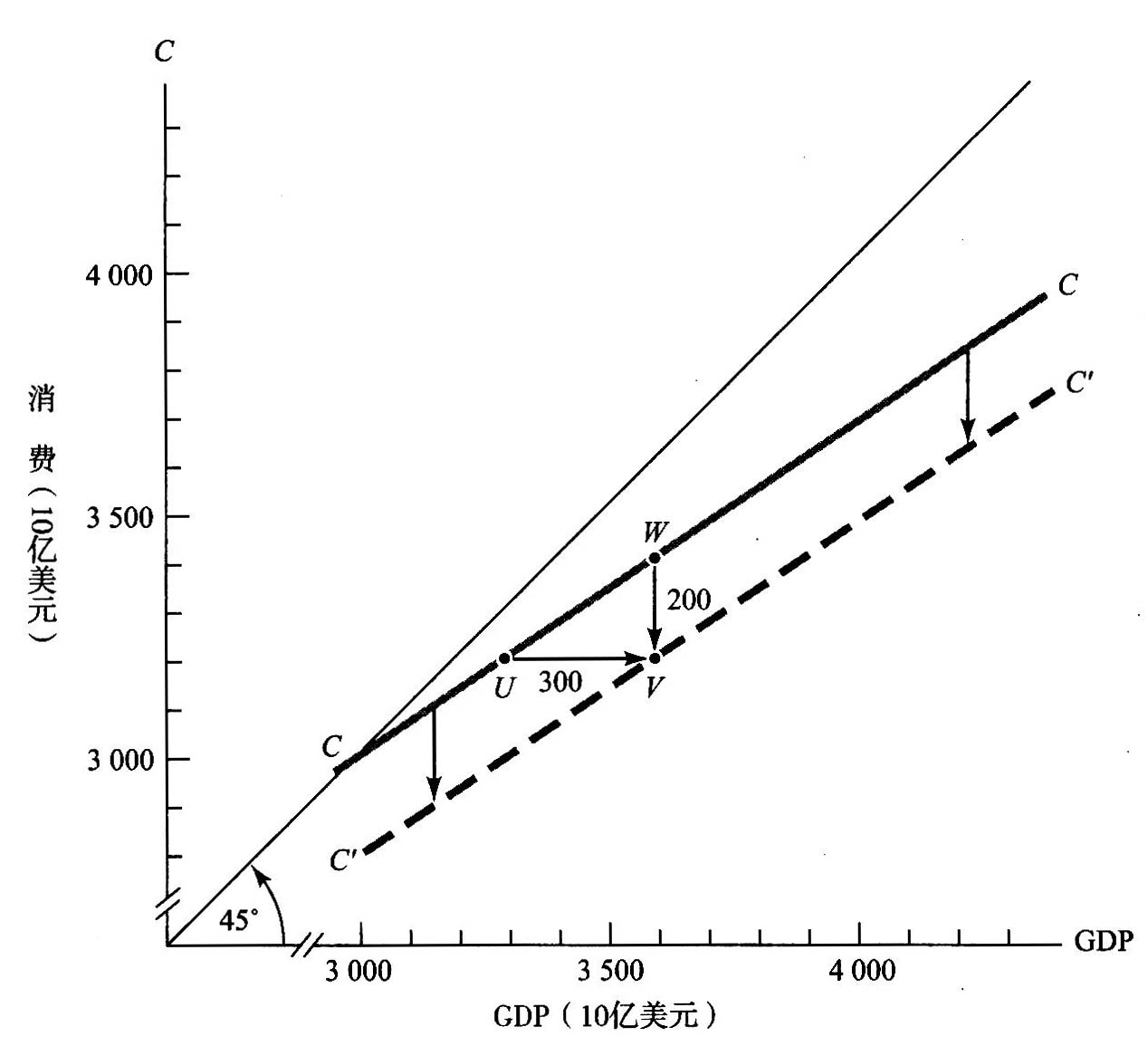
图24-6  税收减少可支配收入，使曲线向右下方移动

每1美元税收会使CC曲线向右移动1美元。CC曲线的右移也意味着CC曲线的下降，但向下移动的幅度小于向右移动的幅度。这是为什么呢？因为向下的移动幅度等于向右的移动幅度乘以MPC。因此，如果MPC为2/3,向下移动的幅度就是2/3x3000亿美元=2000亿美元。请你证明=2/3UV。

征税对总需求的影响

为什么政府征税会降低总需求和GDP的水平？增加税收会减少我们的可支配收人，而可支配收人的降低又会使我们减少消费。很明显，如果投资和政府支出保持不变，那么消费支出的减少将会降低GDP和就业水平。因此，在乘数模型中，增加税收而不增加政府支出，将会降低实际GDP。[ 4 ]

回过去看看图24-6就能知道这其中的原因。该图中，上方的CC曲线代表不存在税收时消费函数的水平。但这一曲线还不是消费函数，因为消费者的收人必须纳税。假定不沦在何种收人水平上，消费者所交纳的税收都是3000亿美元；这样，在每个产出水平，）都正好比GDP少3000亿美元。如图24-6所示，这一税收数量可以用消费曲线向右移动3000亿美兀来表亦。这一向右的移动还可以表现为向下的移动；如果为2/3，那么向右移动3000亿美元就可以视为向下移动2000亿美元。

在我们的乘数模型中，税收无疑会降低产出。图24-7说明了这一点。当税收增加时，I+G保持不变，但税收的增加将会降低可支配收人，从而使消费曲线CC向下移动。因此，C+I+G曲线也会向下移动。你可以用铅笔在图24-7中画一条新的较低的C'+I+G线。证实该线与45°线的新交点，必然是一个较低的GDP均衡水平。

请注意，G是政府在商品和服务上的支出。它不包括转移支付，如失业保险或社会保障等项。这些转移支付被视为负税收。因此，最好将这里所考虑的税收（T）看成是税收减去转移支付。这样，如果直接税和间接税总额为4000亿美元，而所有的转移支付为1000亿美元，那么净税收r就等于4000亿美元-1000亿美元=3000亿美元。（你能否看出：为什么社会保障增加会降低T而增加DI），从而使C+I+G曲线向上移动并且使GDP的均衡水平增加吗?）

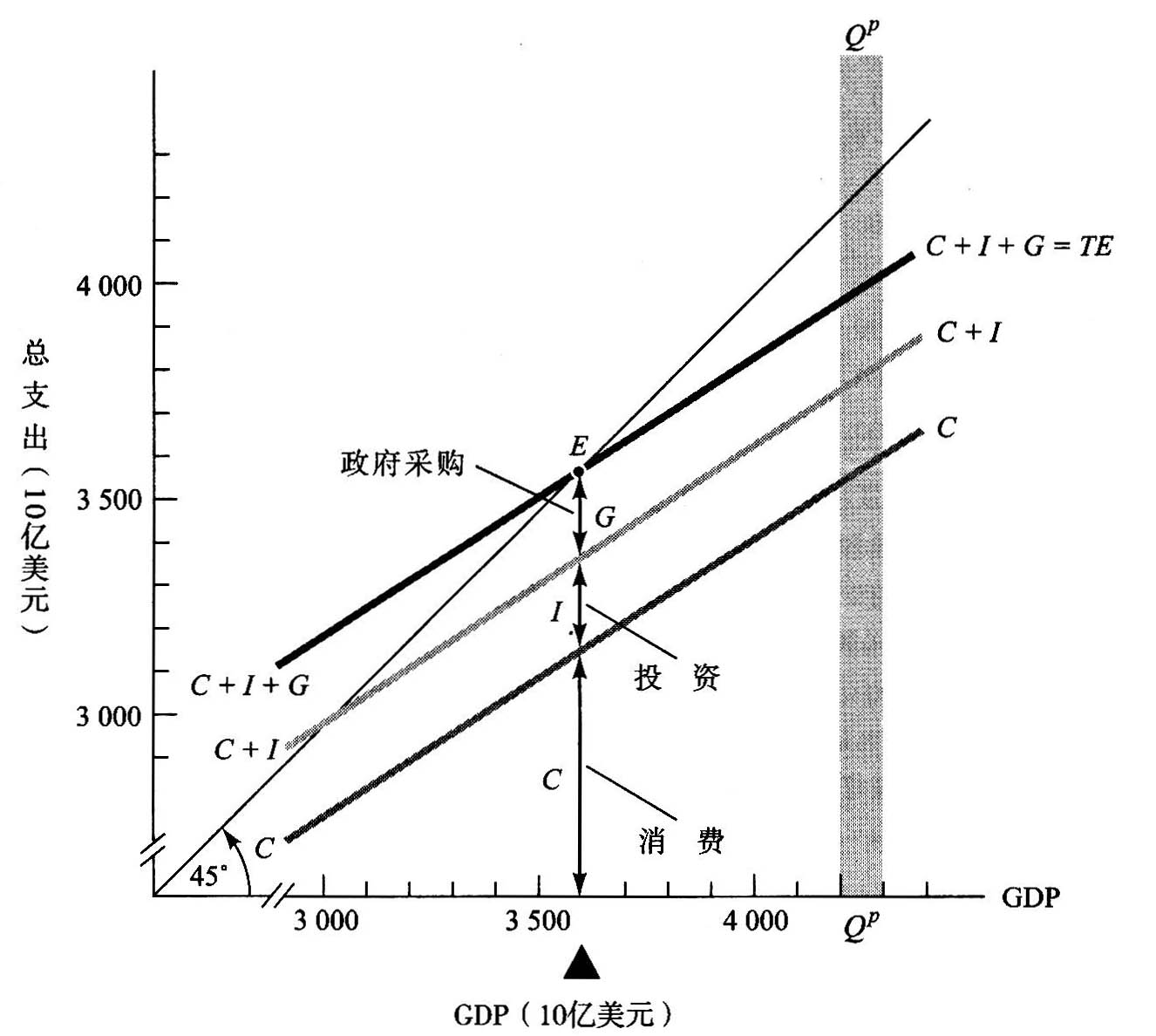
图24-7  把政府采购像投资那样加上去以决定均衡GDP

现在在消费支出与投资支出之上，我们加上政府在商品和服务上的支出。这使我们得到新的总计划支出曲线，汉=C+I+G。在该曲线与45°线的交点E上，我们得到了GDP的均衡水平。

数值例子

以上论点在表24-2中都能得到说明。该表非常类似于说明在最简单乘数模型中的产出决定的表24-1。表24-2的第U）栏表示GDP初始水平，第（2）栏表示固定税收3000亿美元；第（3）栏的可支配收入等于GDP减去税收；第（4）栏为计划消费量，它是）的函数；第（5）栏是固定计划投资数量；第（6）栏为政府支出水平；第（7）栏为计划支出总量，7E，等于第（4）栏至第（6）栏之和，即C+J+G。

最后，我们对比第（7）栏的总意愿支出量跟与第（1）栏的GDP初始水平。如果意愿支出量高于GDP，厂商为适应支出水平将增加产量，于是产出增长；如果意愿支出量低于GDP，则产出下降。这种趋势，如最后一栏所示，会使我们确信，产出一定会在36000亿美元的水平上达到均衡。

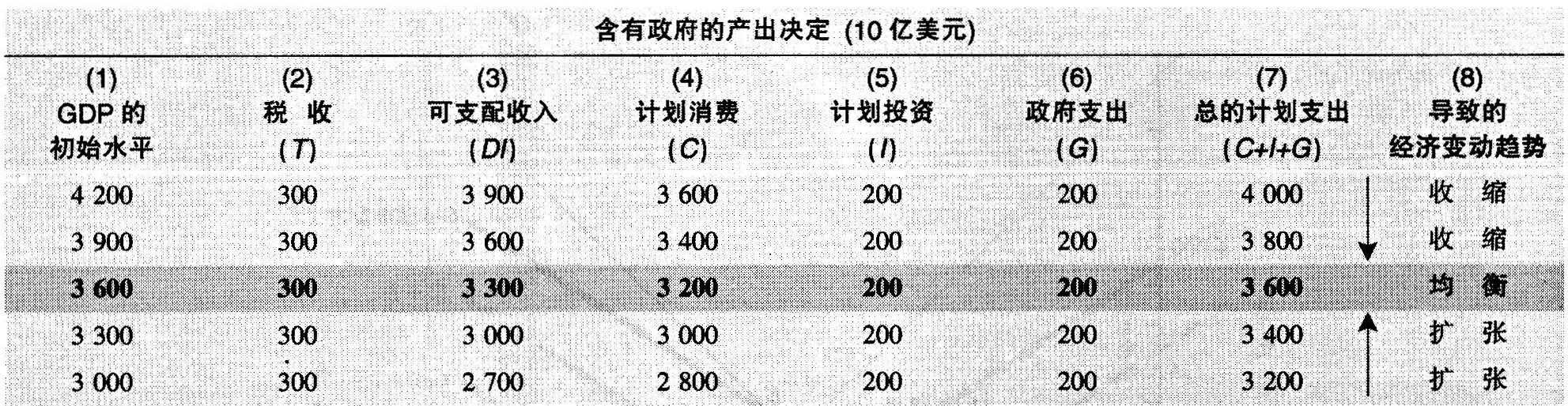
表24-2  政府支出、税收及投资决定均衡GDP

由表可见，当把政府在商品和服务上的支出加人到乘数模型中的时候，产出将如何决定。在这个例子中，税收是“一次总付”的或不受收入水平影响的。因此可支配收人等于GDP减3000亿美元。总支出等于I+C+C(由消费函数所决定的消费)。

在产出水平小于36000亿美元的两行中，计划支出量大于产出量，因而产出会扩张。而产出水平大于36000亿美元的两行也是难以持久的，并会导致收缩。只有在产出水平为36000亿美元时才达到均衡产量，即计划支出量等于产出量。

财政政策乘数

乘数分析说明：政府财政政策是一种作用与投资十分相似的高能支出。投资与财政政策之间的相似性说明，财政政策对于产出量也应具有乘数效应。这一点无疑非常正确。

政府支出乘数（government expenditure multiplier）是指政府在产品和服务上每增加1美元开支所能引起的GDP的更多增长的程度。政府在商品或服务上的一项采购，会引致一系列的再支出：如果政府修一条公路，修路工将会用其收人的一部分购买消费品；这又会接着引起出售消费品的人收人的增加，而增加的收入的一部分又会被花掉。在所考查的简单模型中，G每增加1美元对GDP的最终效果与每增加1美元的效果是一样的：即乘数为1/（1-MPC）。图24-8说明G的变动如何导致GDP的更髙水平，而且GDP增长额会数倍于政府购买量的增加额。

为说明政府每多花1000亿美元所产生的影响，图24-8中的C+I+G曲线向上移动了1000亿美元。GDP的最终增加量则等于最初支出的1000亿美元乘以支出乘数。在这个例子中，由于MPC为2/3，乘数是3，所以均衡的GDP水平增加3000亿美元。

这个例子及常识告诉我们，政府支出乘数和投资乘数是完全相同的，它们被统称为支出乘数（expenditure mul-tiplier）。

请注意，乘数具有双向作用。如果政府开支下降，而税收和其他因素保持不变，GDP的下降幅度将等于C的变化量乘以乘数。

G对产出的影响也可以从表24-2中的数据例子说明，你可以用铅笔填入一个不同的G，比如说3000亿美元，并找出GDP的均衡水平。它会给出与图24-8相同的答案。

小结

政府在产品和服务上的支出（G）是决定产出和就业的一个重要因素。在乘数模型中，如果G增加，那么产出的增加幅度就是G的增加量乘以支出乘数。因此，政府开支就具有了一种通过抑制或刺激产出而影响商业周期波动的潜能。

战争对于充分就业是必需的吗

历史上，经济的扩张始终伴随着战争。从表24-3中可以看出，过去主要的战争通常都伴随着军事开支的大量增长。例如，在二战期间，在1941年12月日本轰炸珍珠港之前，。国防支出费用占GDP；

的比重增加近10%。实际上，很多学者都认为，美国经济从大箫条中崛起主要是因为二战所带来的军备扩张。同样的但规模较小的朝鲜战争和越南战争中，类似的经济扩。张也存在着。

不过，上世纪90年代#的海湾战争却曾经导致了—场经济衰退。出现这种反常的原因在于当时的军事开支的增加非常有限，而战争所导致的心理因素的负作用选选超过if玫府文出增长的作用。

这些心理因素是什么呢？1990年8月伊拉克入侵科威特之后，消费者和投资者变得恐慌起来，进而减少了他们的支出。此外，国际油价飚升也降低了八们的实际收入。直到1991年2月美国迅速取胜之后，这些心理因素才得以矫正。

那么2003年初伊拉克战争的影响又是怎样的呢？这场战争不像历史上的大多数大战，而是更类似于海湾战争。战争时期美国在国防上的开支几乎没有什么增长，而同期却一直伴随着高涨的国际原油价格，消费者和企业投资者的谨小慎微共同到起了一场阻挡经济前进的顶头风。

战时支出对经济扩张的作用是关于乘数模型功能的最为直接和最有说服力的案例^一。确保你已经理解了这个潜在的机制，即为什么经济扩张的规模如表24-3所示的那样有所不同。

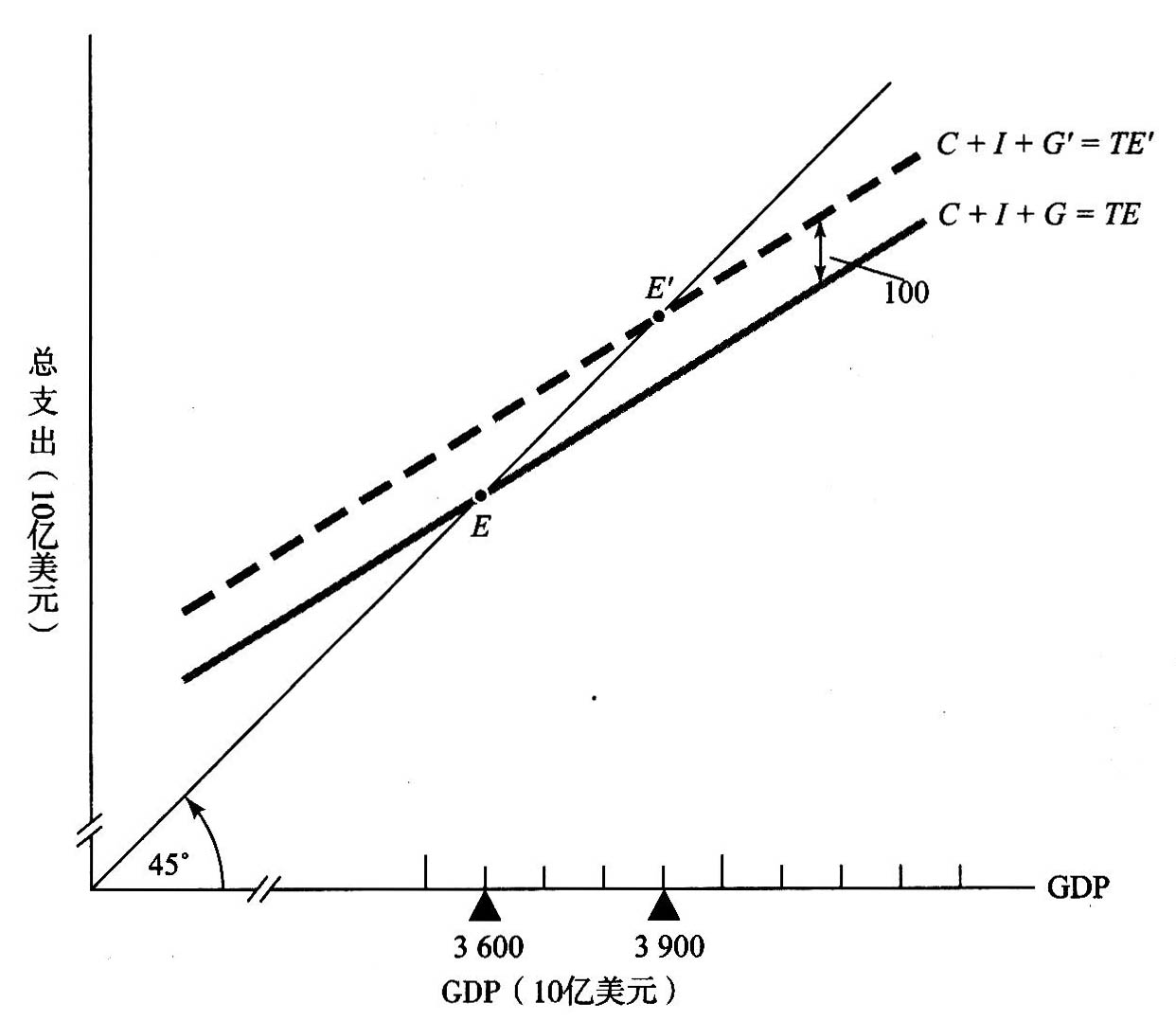
图24-8  增加G对产出的影响

假设政府增加了1000亿美元的国防开支，以对付中东油田所面临的威胁。这使得C+I+G曲线向上移动了1000亿美元，成为C+I+G'。

这时新的均衡GDP水平处于45°线上的f点，而不是E点。由于MPC为2/3,新的产出水平增加了3000亿美元。这就是说，政府支出乘数为：

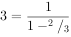
(如果MPC为3/4或9/10,那么政府支出乘数将会是多少呢?)

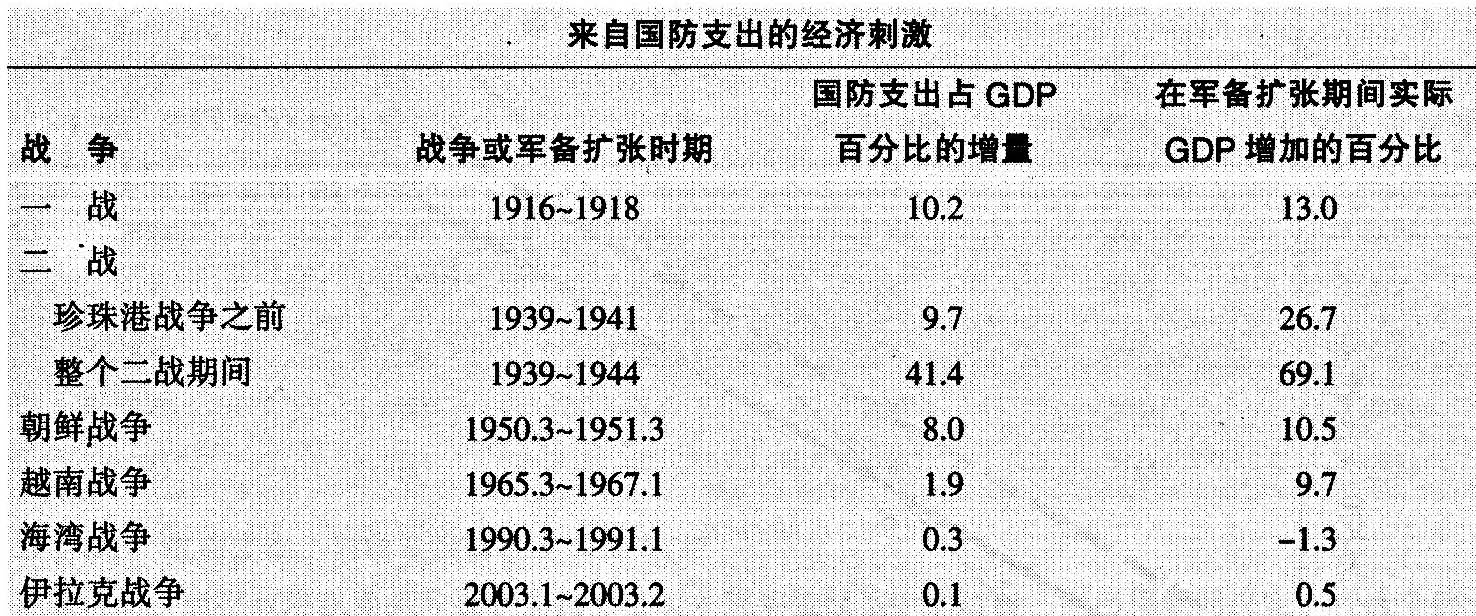
表24-3  经济繁荣伴随着军事开支的大规模增长

由表可见，战争或军备扩张时期，军备扩张的规模及由此产生的实际GDP的增长。那些主要的战争都曾产生了持续的经济繁荣，但是由于其他部门的反作用，近20年来的小规模战争都导致了经济增长的减速。

资料来源：Department of Commerce,National Income and Product Accounts,available at www.bea.gov,and  estimates by authors.

税收的影响

税收也会影响GDP均衡水平，尽管与支出乘数相比税收乘数要小一些。考虑这样一个例子：假设经济正处于其潜在GDP水平，这时国家增加了2000亿美元的国防开支。这种突然增加国防开支的情况在美国历史上可谓屡见不鲜：20世纪40年代早期是因为第二次世界大战，1951年是因为朝鲜战争，60年代中期是因为越南战争，而80年代早期里根执政期间是由于美苏军备竞赛。再假设经济规划者希望通过增加税收，来抵消增加2000亿美元的政府开支（G）对GDP所产生的影响。那么税收应该增加多少呢？

我们肯定要大吃一惊。为了抵消G增加2000亿美元的影响，我们需要增加的税收将大于2000亿美元。在以下数字例子中，我们可以从图24-6中找出税收（或T）增加的准确数量。该图说明r增加3000亿美元会使可支配收人减少，并且MPC在为2/3时导致消费量正好下降2000亿美元。换句话说，增加3000亿美元税收将会使CC曲线向下移动2000亿美元。这就是说，虽然国防开支增加10亿美元可以使C++G线向上移动10亿美元，但税收增加10亿美元却只能使C++G曲线向下移动10亿美元的2/3（当MPC为2/3时）。因此，要抵消国防开支增加所产生的影响，就需要T比G有更大幅度的增加。

在影响产出方面，变动税收是个有力的工具。但是税收乘数小于支出乘数，小的幅度为一个MPC因子，即：

税收乘数=MPCx支出乘数

府在G上支出1美元时，这1美元会直接花费在GDP上。而另一方面，当政府减少1美元税收时，这1美元只有一部分花费在C上，另一部分则会被储蓄起来。这种对1美元的G和1美元的T所做出的不同反应，就足以使税收乘数低于支出乘数。[ 5 ]

实践中的财政政策

肯尼迪总统在1961年采用了凯恩斯主义经济学的观点，使财政政策成为美国对付衰退和通货膨胀的一个主要的武器。肯尼迪总统提出大幅度削减税收来帮助经济走出低谷。这些措施实施后，美国经济开始迅速增长。但是，减税再加上1965~1966年越战中财政扩张的影响，又使得产出增长过快，超过了潜在的GDP水平，于是通货膨胀开始升温。为了对付不断上升的通货膨胀，并抵消越战所增开支的影响，1968年国会批准了开征一项临时性的收人附加税。

20世纪80年代的美国是另一个反映财政政策如何运行的戏剧化的例子。1981年国会通过了里根总统提出的“供应方减税”（supply-side tax cuts）等经济复兴计划，其中也包括大量增长国防开支。这些措施将美国经济从1981~1982年的严重衰退中拯救出来。

20世纪80年代中期的新财政政策开启了一个崭新的纪元。里根的财政政策导致政府预算赤字（财政的收人和支出之差）急剧增大，在整个80年代政府赤字和债务都在以极快的速度攀升。在这个预算赤字的时期，由于国会挣扎于削减赤字的斗争中，致使新的政府措施迟迟不能出台。

克林顿总统1993年一上台，就面临着一个痛苦的财政两难困境：一方面高赤字依然顽固地存在着；另一方面经济不景气且失业率高得令人难以接受。总统是应该先处理赤字，通过增加税收、降低支出来增加公共储蓄，进而靠储蓄水平提高来带动国民储蓄和投资的增长呢？还是应该关注财政紧缩会减少C+I+G并“挤出”投资，而税收增加和G的减少又会降低产出？

在两难困境中争斗之后，克林顿总统还是决定优先考虑削减财政赤字。1993年预算法案决定，在今后5年中减少联邦赤字1500亿美元（或GDP的2%）。这些举措使得开支收缩，税收增加，一个空前繁荣的经济和高水平的股票价格同时出现，随之而来的是始自1998年的预算盈余，着实令所有的专家都深感惊讶。

然而，财政盈余所维持年份是很有限的。不尽人意的股市下跌、经济衰退、战争和恐怖主义等一系列冲击，共同导致了美国政府财政状况迅速恶化。在这种情况下，乔治·W·布什总统在2001年劝说国会通过大规模全面减税的法案，并废除了遗产税（尽管只是临时而非永久性的）。另一项关于减税的规定于2003年制定，即降低对股息的征税，以减轻美国人的资本税负担。

伴随着布什政府的减税计划，美国经济经历了一个比较完整的周期。财政政策不再作为主要的反经济周期的手段。相反，经济学家认识到，税收的变动应当主要集中于影响国民储蓄、投资和创新等经济活动。

稳定政策的另一手段

到目前为止，我们的乘数分析的着重点，还只是将它作为一种稳定经济的财政政策的工具。但凯恩斯主义经济学家强调的财政政策，却仅仅是对付商业周期的可行性的方法之一。政府还有另外一个具有同样威力的武器：货币政策。尽管货币政策的作用方式与财政政策大不相同，但如同我们在下面两章中将要看到的那样，它作为一种政策在解决失业和通货膨胀方面的确同样具有许多优点。

正如火车的两个车头（有时朝这个方向开，有时又朝另一个方向开），在短期内，货币政策和财政政策都是带动产出、就业和价格的强有力的引擎。

现实中的乘数

现实地把握乘数的数值是诊断经济和制定对策的关键。医生用止痛药必须知道不同剂量的效果，同理，经济学家也必须知道支出乘数和税收乘数的数值的大小。当经济增长过快而必须开出财政政策的猛药时，经济的诊治者在决定使用多大剂量的“增加税收”或“减少开支”时，需知道实际的乘数究竟有多大。

教科书上的模型所给出的是关于宏观经济结构的高度简化的图形。为获得更符合现实的、反映产出随政府开支的变动而变动，的模型，经济学家需要建立大型的经济计量模型（见第23章有关讨论），并通过计算政府开支变动对经济的影响在模型中进行数值检验。这样，模型就可以作为提出政策建议的理论根据。这些大型模型不但包括我们已经介绍的显而易见的因素，而且还应包括我们此后将会考虑到的因素，诸如，一种更现实的税收处理方法，一个健全的货币政策部门，还有工资和价格的变动，等等。这些因素的加入会减小乘数的数值。

美国最近有一项综合性的经济计量研究，提供了一个有代表性的乘数估算方法。该模型包含了一套预测所有各主要部门经济行为（包括货币金融部门以及投资需求函数和消费函数）的方程式，并与其他涉外部门形成一套完整的体系。在一系列的参数中，假定政府的商品和服务采购的实际水平的增加额始终为10亿美元。模型就会据此计算政府支出这个增加量对实际GDP的影响。由政府支出增加所引起的实际GDP的变动，可以提供一个政府支出乘数的估计值。

图24-9显示了这一研究结果。最粗的线代表由8个模型所估算出的政府支出乘数的平均数，而其余的细线则表示每个模型的估算结果。第一、第二年乘数的平均值约为1.4；但此后，随着货币因素和国际因素开始起作用，乘数趋向于缓慢下降。（货币因素是指GDP的增加对利率所产生的影响，正如我们在以后将要说明的，这种影响会对投资产生挤出效应。）

这些估算的一个有趣之处是，不同的模型（图24-9中的8条细线表示）所估算出的乘数具有相当大的差异。为什么估计值会不同呢？首先，经济关系本身存在着固有的不确定性。当然，自然或社会结构的不确定性恰恰是科学引人人胜和令人激动的源泉；如果每一件事都确凿无疑，那么科学家们就要失业了。但由于经济学家不可能在实验室中进行那种可以控制的实验，因此，对经济体系的研究就更加地具有挑战性。更令人迷惑的问题是，经济本身会随着时间的推移而发生变化。因此，对1965年来说是“正确”的模型，对2005年来说就可能与“正确”相去甚远。

此外，经济学家对宏观经济的基本属性的认识也存在着完全不同的观点。一些经济学家相信凯恩斯主义的方法最适合于解释宏观经济行为，而另一些经济学家则认为古典理论或真实商业周期理论更具有洞察力。由于所有这些不确定性和不同观点的存在，经济学家们对于乘数有不同的估计也就不足为奇了。

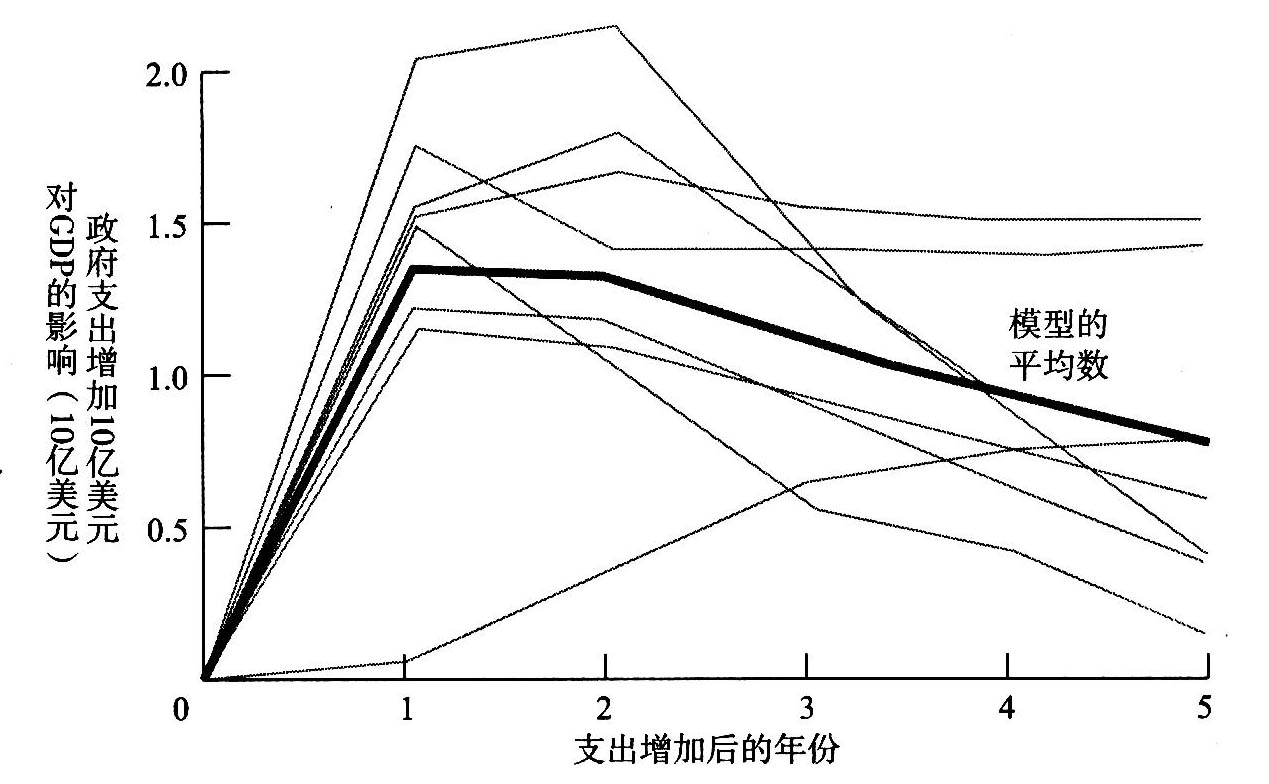
图24-9  宏观经济模型中的支出乘数

一项详细的研究显示了运用不同的宏观经济模型所估算的政府支出乘数。这些实验说明：政府用于购买商品和服务的实际支出增加10亿美元，可能会给不同时期的实际GDP造成多大的影响。这就是说，所说明的是：G的10亿美元的变动对Q产生的影响。粗线表示不同模型的平均乘数，而细线则表示每一个模型的乘数。

资料来源：Ralph C.Bryant，Gerald Holtham，and Peter Hooper," Consensus and Diversity in Model Simulations" in Empirical Macroeconomics for Interdependent Economies (Brookings Institution,Washing-ton,D.C.,1988).

乘数模型的背后

我们已经研究了凯恩斯主义乘数模型的最基本的应用。对于理解商业周期、政府财政政策与国民产出之间的联系，这种分析提供了必不可少的帮助。

但是不要错误地认为，只要简单地教会鹦鹉学会说“C+I+G”或者“某某乘数”鹦鹉就会变为一个宏观经济学家，那样可就大错特错了。理解宏观经济要求不仅要理解各种模型，而且要理解各模型的优势和劣势。现将最简单乘数模型小结如下：

●乘数模型忽略了货币和信用对消费和投资的影响。

●最简单的乘数模型忽略了对外贸易对国内国外产出的影响。

●总供给也未在考虑之列，所以我们无法分析支出的扩大如何分布在价格和产量之上。

这些问题并非无关紧要，相反，它们是理解现代宏观经济学的关键之所在。在接下来的几章中，我们将引人更加现实的要素。一旦将货币和利率的影响、工资和价格变动纳人分析，我们就会看到财政政策对经济的影响可能会与最简单的乘数模型的表现大不相同。

我们接下来要转向分析经济学中最有趣的内容之一：对货币的研究。一旦理解了中央银行如何决定货币供给，那么，我们就会更完整地看到，政府怎样才能驯服那些在资本主义大部分历史时期中一直是狂暴不羁的商业周期。

总结提要

A.基本乘数模型

1.乘数模型提供了一种理解总需求对产出影响的简明的方法。在这个最简单的方法中，居民户消费是可支配收人的一个函数，而投资则是一个固定不变的量。人们的消费愿望和企业的投资意愿通过产出的变动而得到平衡。国民产出的均衡水平必然处于储蓄曲线SS和投资曲线II的交点。用投人一产出的分析方法我们也可以得到这一结论，均衡产量出现于总支出（TE），即消费加投资曲线（TE=C+I）与45°线的交点处。

2.如果产出暂时地高于均衡水平，则企业将会发现其产出量大于销售量，而产品存货将会非自愿地堆积起来，利润也会骤减。因此，厂商势必要削减生产、解雇工人，使产量回到均衡水平。惟一能够维持的产量水平，是当买方自愿的购买量正好等于企业所愿意生产的数量时才能达到。

3.因此，在简化了的凯恩斯乘数模型中，乐曲的基调是由投资来决定，而消费则按这个音乐起舞。投资决定产出，而储蓄则被动地对收人的变化做出反应。产出会上升或下降，直至计划储蓄已经调整到与计划投资相等的水平为止。

4.投资对产出有乘数效应。当投资增加时，产量将首先增长相同的数量。但是，当资本品产业的收人获得者得到更多的收人时，他们便会启动一系列由此引致的一系列次轮消费支出和就业。

如果人们总是把所增加的每1美元收人中的r用来购买消费品的话，那么乘数链条的总和将是：

1+r+r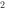+…=1（1-r）=1/（1-MPC）=1/MPS

从数字上看，最简单的乘数等于MRS的倒数，或者：1/（1-MPC）。乘数可以向任一方向起作用，它既可以成倍地增加投资，也可以成倍地减少投资。之所以会有这样的结论，是因为要想使储蓄增加1美元，收人的增加必须总是大于1美元。

5.需要着重记住的几点是：（a）基本的乘数模型强调总需求变动对产出和收人影响的重要性。（b）它一般适用于有闲置资源存在的情况。

B.乘数模型中的财政政策

6.对财政政策所做的分析，详细讲解了凯恩斯乘数模型。它说明了政府开支增加并在税收和投资不变的条件下就其本身而论就像投资增加一样对国民产出有扩张效应。总支出TE=（C+I+G曲线会向上移动，与45°线相交于更高的均衡点。

7.在投资和政府开支不变的条件下，税收的减少就其本身而论，会提高国家产出的均衡水平。对照GDP而作出的CC消费曲线，因税收的削减而向上和向左移动。但是，由于新增可支配收人中有一部分被用于储蓄，因此用于消费的新增货币，将没有新增的可支配收人那么多。所以，税收乘数要小于政府支出乘数。

8.运用统计技术和宏观经济学理论，经济学家们发展了估算支出乘数的现实模型。用主流的方法估计，所测定的4年内的乘数值是在1~1.5之间。

概念复习

基本乘数模型

TE=C+I曲线

TE=C+I+G曲线

决定GDP的两种方法：

计划储蓄=jihuatouzi计划C+计划I=计划GDP

投资等于储蓄：计划水平与实际水平

投资的乘数效应

乘数

=1+MPC+（MPC）+…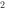

=1/（1-MPC）=1/MPS

政府采购和税收

财政政策：

G对均衡GDP的影响

T对CC和GDP的影响

政府采购（G）和税收（T）的乘数效应

C+I+G曲线

现实总乘数估计

补充读物和互联网站

补充读物

The multiplier model was developed by John Maynard Keynes in The General Theory of Employment,Interest and Money (Harcourt,New York,first published in1935).Advanced treatments can be found in the intermediate text-books listed in the Further Reading section in Chapter 20.

互联网站

Brad DeLong of the University of California at Berkeley has a Web page with many references to Keynes.See www.j-bradford-delong.net/Index.html.One of Keynes’s most influ-ential books,The Economic Consequences of the Peace (1919),predicted with uncanny accuracy that the Treaty of Versailles would lead to disastrous consequences for Europe-it is available at www.socsci.mcmaster.ca/~econ/ugcm/3113/keynes/peace.Writings  on Keynesian economics and many other current subjects can be found on Paul Krugman’s website atwww.wws.princeton.edu/~pkrugman/.

问题讨论

1.简单的乘数模型中，假设投资总是等于零。说明在这种特殊情况下均衡产出将出现于消费函数的收支相抵点。为什么当投资量为正时，均衡产出将高于该消费函数的盈亏平衡点？

2.仔细定义什么是乘数模型中的均衡？在下列情形中分别解释为什么该情况不是一种均衡？同时描绘在每一种情况下，整个经济会如何反应以重新达到均衡？

a.在表24-1中，GDP为33000亿美元。

b.在图24-2中，实际投资为零。

c.汽车销售商发现他们的存货远远大于他们的计划。

d.在A部分最简单的模型中，消费者计划储蓄600美元，同时商人们计划投资700美元。

3.重新设制表24-1，假设计划投资等于（a）3000亿美元，（b）4000亿美元；则GDP的最终差额是多少？这个差额比的变动大还是比它小？为什么？当从2000亿美元下降到1000亿美元时，GDP必然会下降多少？

4.请给出乘数的（a）—般定义，（b）算式，（c）几何图形。当分别等于0.9，0.8，0.5时，或MPS分别等于0.1或0.8时，算出乘数的数值。

5.我们已经知道，投资会经由加速数原理（见第23章）、随着产出的变化而变化。我们可以定义边际投资倾向（MPI），表示每一单位产出变化所引起的投资的变化。假设投资为：I=I+1.2Q（MPI=1.2），当MPC为0.8时，边际支出倾向为什么等于MPC+MPI？算出当边际支出倾向等于2时，支出和再支出的数列。试解释发散的无穷几何级数的经济意义。

6.运用支出的系列“轮”数或曰级数方法，用文字说明为什么税收乘数小于支出乘数。

7.解释为什么政府有可能运用财政政策来稳定经济。为什么财政政策在“凯恩斯区域”对于提高产出是有效的，而在总供给为垂直线的经济中则是无效的？

8.“即使政府花费数十亿美元用于浪费性的军备，这一行为在衰退时期也能够创造就业。”请对这句话加以讨论。

9.储蓄和投资图以及45°线和曲线C+I是用来解释在乘数模型中国家产出是如何被决定的两种方法。请描述，这两种方法，并解释为什么它们的效果是一样的。

10.有难度的问题：国民产出的增长主要依靠储蓄和投资，并且我们从小就受到教育并笃信勤俭节约重要，“省下来的一分钱就是赚到的一分钱”储蓄得越多对经济就越有利吗？在一次饶有兴趣的争论（称为节约悖论）中，凯恩斯指出：当人们想储蓄得更多时，其结果并不意味着整个国家能够储蓄得更多。

根据这个观点，假设人们决定储蓄得更多时的情况。用图24-4中的乘数模型说明它是怎样使SS曲线向上移动的。解释它为什么会降低产出而不是增加了储蓄。直觉上，假如在一个给定的商业环境中，人们试图增加储蓄，降低消费，销售量就会下降，厂商就会减少生产。请解释产量会下降多少。这就是节约的悖论：当集体决定储蓄得更多时，其结果却会导致产出和收人的减少，而储蓄并不增加。

请解释：为什么说这是人们的成见中存有谬误的好例子。进一步解释：为什么悖论只在经济中存在着闲置资源时才能成立，而在典型的完全就业的经济中，储蓄的增长又确实能够带来投资的增加而不是产出的下降。

注：

[ 1 ]我们一开始将图形简化，不包含税收、未分配的公司利润、外贸、折旧和政府财政政策等因素。目前，我们假定收人就是可支配收人，它等于GDP。

[ 2 ] 无穷几何级数的公式是：

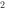1+r+r+r+…+r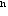+…=1/(1-r)

其中MPC(r)的绝对值小于1。

[ 3 ] 通过改动表24-1中的数字也可以说明这个答案。在第(4)栏中我们现在填人3000亿美元，而不是原有的2000亿。结果表明新的均衡产出水平由原来的均衡水平又向上移动了一行。你能否说明当投资数量减少时乘数如何发生作用？

[ 4 ] 严格地说，本章提到的税收指的是净税额，即税收额减去转移支付。

[ 5 ] 为了简化，我们取税收乘数的绝对值（由于该乘数实际为负值）。我们可以通过前面所列出的“支出的系列轮数”方法来说明不同的乘数。假设MPC为r,那么如果G上升一个单位,支出的总增加额就是各轮再支出的总和：

1+r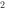+r+r+…=

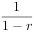
现在，如果税收减少1美元，那么消费者新增加的可支配收入的（1-r)倍会用于储蓄，并在第一次支出中花掉r美元,在以后各次中，总支出便是：

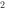r+r+r+…=

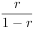
因此，税收乘数是r倍的支出乘数，而这里的r是MPC。