阿基米德(古希腊文：Yˉㄐㄧˉㄇㄧˇㄉㄜˊ)（公元前287年—公元前212年），古希腊哲学家、数学家、物理学家。出生于西西里岛的叙拉古。

阿基米德到过亚历山大里亚，据说他就在亚历山大里亚时期发明了阿基米德式螺旋抽水机。

后来阿基米德成为兼数学家与力学家的伟大学者，并且享有“力学之父”的美称。

阿基米德流传于世的数学著作有10余种，多为希腊文手稿。

Ἀρχιμήδης

Archimedes of Syracuse

阿基米德

 c. 287 BC – c. 212 BC

力学和流体静力学的起源应该到实用技术中去寻找，而不应到早期希腊哲学家的著作中去寻找，但是当观察同在几何学中学到的演绎方法结合起来的时候，这两门科学就有了坚实的基础。把这两门科学放在坚实基础上的第一人正是阿基米德。他的工作比任何别的希腊人的工作都更具有把数学和实验研究结合起来的真正现代精神。在结合的时候，只解决一定的有限的问题，提出假说只是为了求得它们的逻辑推论，这种推论最初是用演绎方法求得的，然后又用观察或实验方法加以检验。

杠杆的实际应用一定是太古时代的事情了，在阿基米德的时代以前两千年，亚述和埃及的雕塑中已经有这方面的例证。今天，我们把杠杆定律看做是一件要由实验决定的问题，而且还从这个定律中推出更为复杂的结果来。阿基米德得却是凭着希腊人对于抽象推理的热爱，从他所谓的不证自明的公理或用简单实验可以证明的命题中得出杠杆原理的。这两个公理和命题就是：

（1）同重的物体放在和支点距离相等的地方，就保持平衡；

（2）同重的物体放在和支点距离不等的地方，就不相平衡，其离支点较远的一端必定下坠。

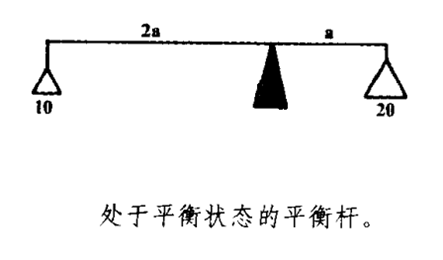
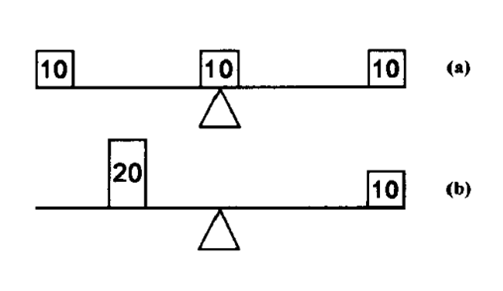
这两条作为“不证自明”的初始前提的“公理”是借助几何的对称和直观建立起来的，就其涵义来说，已经包含有杠杆原则，或与杠杆原理是一回事的重心原理。但是，把杠杆定律和当时人认为比较简单的道理统一起来，却是前进了一步。事实上，这就是最科学的解释的典型。因为科学解释按其本质来说，一般也就是用我们的心灵比较熟悉的现象来说明新的现象。   

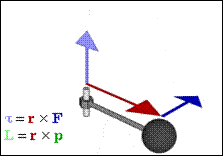
现代科学与工程技术中所使用的力矩（torque）的概念，起源于阿基米德对杠杆（lever）的研究。

大概在他九岁时，父亲送他到埃及的亚历山大城念书，亚历山大城是当时西方世界的知识、文化中心，学者云集，举凡文学、数学、天文学、医学的研究都很发达，阿基米德在这里跟随许多的数学家学习，包括几何学大师欧几里得，因此奠定了他日后从事科学研究的基础。阿基米德是第一位讲科学的工程师，在他的研究中，使用欧几里得的方法，先假设，再以严谨的逻辑推论得到结果，他不断地寻求一般性的原则而用于特殊的工程上。他的作品始终融合数学和物理，因此阿基米德也被称为物理学之父。

阿基米德是古代世界的第一位也是最伟大的近代型物理学家。他所发明的作战机械把罗马人阻于叙拉古城外达三年之久，公元前212年城破后，他被一个士兵杀死。到公元前75年，他的坟墓才被当时担任西西里的财政官的西塞罗（Cicero）发现，并加以虔诚的修缮。对于阿基米德来说，机械和物理的研究发明还只是次要的，他比较有兴趣而且投注更多时间的是纯理论上的研究，尤其是在数学和天文方面。在数学方面，他利用“逼近法”算出球面积、球体积、抛物线、椭圆面积，后世的数学家依据这样的“逼近法”加以发展成近代的“微积分”。他更研究出螺旋形曲线的性质，现今的“阿基米德螺线”曲线，就是为纪念他而命名。

阿基米德将欧几里得提出的“穷竭”法作了有效的运用，他提出圆内接多边形和相似圆外切多边形，当边数足够大时，两多边形的周长便一个由上，一个由下的趋近于圆周长。他先用六边形，以后逐次加倍边数，到了九十六边形，求出π的估计值介于3又10/71介于3又1/7之间。

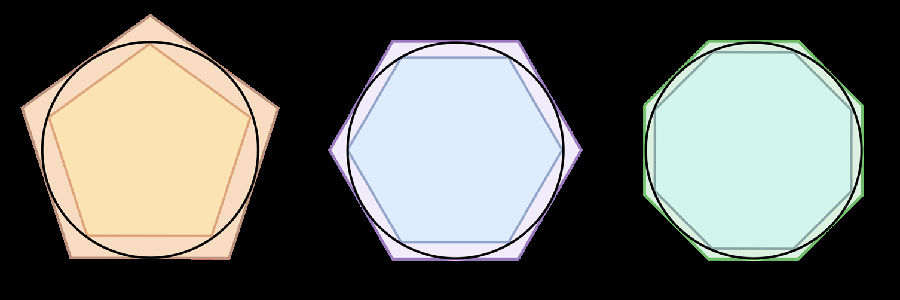
“穷竭”(exhaustion)法测量圆的面积，计算圆周率。

塞莫斯的阿利斯塔克（Aristarchus of Samos，公元前310- 230年左右）是阿基米德的同代人，但较为年长。据阿基米得说，阿利斯塔克还提出一个假说，认为“恒星与太阳是不动的，地球沿着圆周的周边绕太阳运动，太阳则在轨道的中心”。这是史上有记载的首位提倡日心说的天文学者。阿利斯塔克的观点并未被当时的人们理解，并被掩盖在亚里士多德和托勒密的光芒之下。在流传到阿基米德手中的《太阳和月球的大小与距离》（On the Sizes and Distances of the Sun and Moon）一书中，阿利斯塔克非常巧妙地把一些几何学原理运用到这个问题上来。他首先考虑了月食时可以看到的现象，其次又考虑了月半圆时可以看到的现象，然后得出结论说：太阳直径与地球直径之比一定大于19：3，小于43：6，即约为7：1。这个数字当然太小，但是，他的研究原则是不错的，而且他能认识到太阳比地球大，这本身已经是一个惊人的成就了。

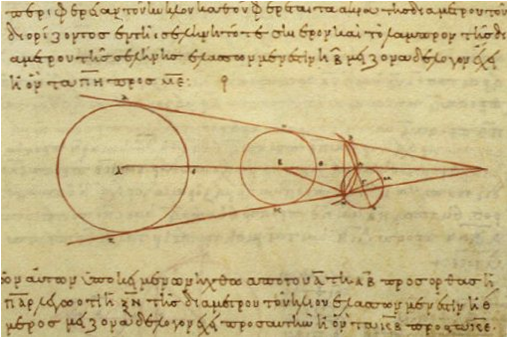
Aristarchus's 3rd century BC calculationson the relative sizes of from left the Sun,Earth and Moon, from a 10th century copy.

奥林匹斯的宗教带有露骨的神人同形同性论色彩，像这样一种宗教与其说是诉诸理智，不如说是诉诸想象力。奥林匹斯正统宗教的这一弱点，加上希腊世界学术观点的基本自由，就促成了一种自然哲学和形而上学的哲学，这种哲学甚至从很早的时代起，就几乎没有受到神学的先入之见的束缚。一千八百年后，经过黑暗时代的混乱局面，在中古时代经院哲学把哲学和神学加以综合、对知识加以改造以后，现代科学的先驱者曾经不得不在一套自圆其说的知识体系的束缚性条件下进行工作。

这套知识体系包括有流行的神学教条和重见天日的亚里斯多德的哲学。这个体系支配着一切人的思想，并且对物理学和生物学问题以及形而上学问题和宗教问题，都给予不容提出异议的解释。