二 逻辑代数基础

一、逻辑电路与运算

1.逻辑代数

在数字逻辑电路中,如果输入变量A、B、C、……的取值确定后，输出变量Ｙ的值也被唯一确定了。称Ｙ是Ａ、Ｂ、Ｃ、……的逻辑函数。逻辑函数的一般表达式可以写作

Y=f(A，B，C，…)

也就是说，如果某逻辑变量Ｙ是由其他逻辑变量Ａ、Ｂ、Ｃ、…经过有限个基本逻辑运算确定的，则Ｙ就是Ａ、Ｂ、Ｃ、…的逻辑函数。

2.基本逻辑运算

1）与逻辑和与运算

通常，我们把结果发生或条件具备用逻辑1表示，结果不发生或条件不具备用逻辑0表示。在此电路中，灯亮和开关接通用逻辑1表示，灯灭和开关断开用逻辑0表示，则可得到表9-3所示的与逻辑真值表。从表中可以看出：当输入A、B都是1时，输出Y才为1，只要输入A或B中有一个为0，输出Y 就为0。可概括为 “有0出0，全1出1”。

2）或逻辑和或运算

当决定某一种结果的所有条件中，只要有一个或一个以上条件得到满足，这个结果就会发生。这种因果关系称为或逻辑关系，简称或逻辑。

3）非逻辑和非运算

A是开关，Y是灯，如果开关闭合，灯就灭，开关断开，灯才亮。当条件不成立时，结果就会发生，条件成立时，结果反而不会发生。这种因果关系称为非逻辑关系，简称非逻辑。

3.复合逻辑运算

1)与非逻辑和与非运算

与非逻辑运算是由与逻辑和非逻辑两种逻辑运算复合而成的一种复合逻辑运算。

2)或非逻辑和或非运算

或非逻辑运算是由或逻辑和非逻辑两种逻辑运算复合而成的一种复合逻辑运算，实现或非逻辑运算的电路称或非门。

3）与或非逻辑和与或非运算

与或非逻辑运算是由与逻辑、或逻辑和非逻辑三种逻辑运算复合而成的一种复合逻辑运算。

4)异或逻辑和异或运算

5)同或逻辑和同或运算

二、逻辑代数的公式化简法

1.逻辑代数基本公式

逻辑代数的基本公式见表9-9。

2．逻辑代数的公式化简法

1）最简与或表达式

对于某一给定的逻辑函数，其真值表是唯一的，但是描述同一个逻辑函数的逻辑表达式却可以是多种多样的。常用的形式有五种：与或表达式、或与表达式、与或非表达式、与非与非表达式、或非或非表达式。

2）公式法化简举例

公式法化简是利用逻辑代数的基本公式、基本规则和常用公式来简化逻辑函数的。常见的方法：并项法，吸收法，消去法，配项法。

三、逻辑代数的卡诺图化简法

1.逻辑变量卡诺图

逻辑变量卡诺图由若干个按一定规律排列起来的最小项方格图组成的。具有n个输入变量的逻辑函数，有2n个最小项，其卡诺图由2n个小方格组成。每个方格和一个最小项相对应，每个方格所代表的最小项的编号，就是其左边和上边二进制码的数值。

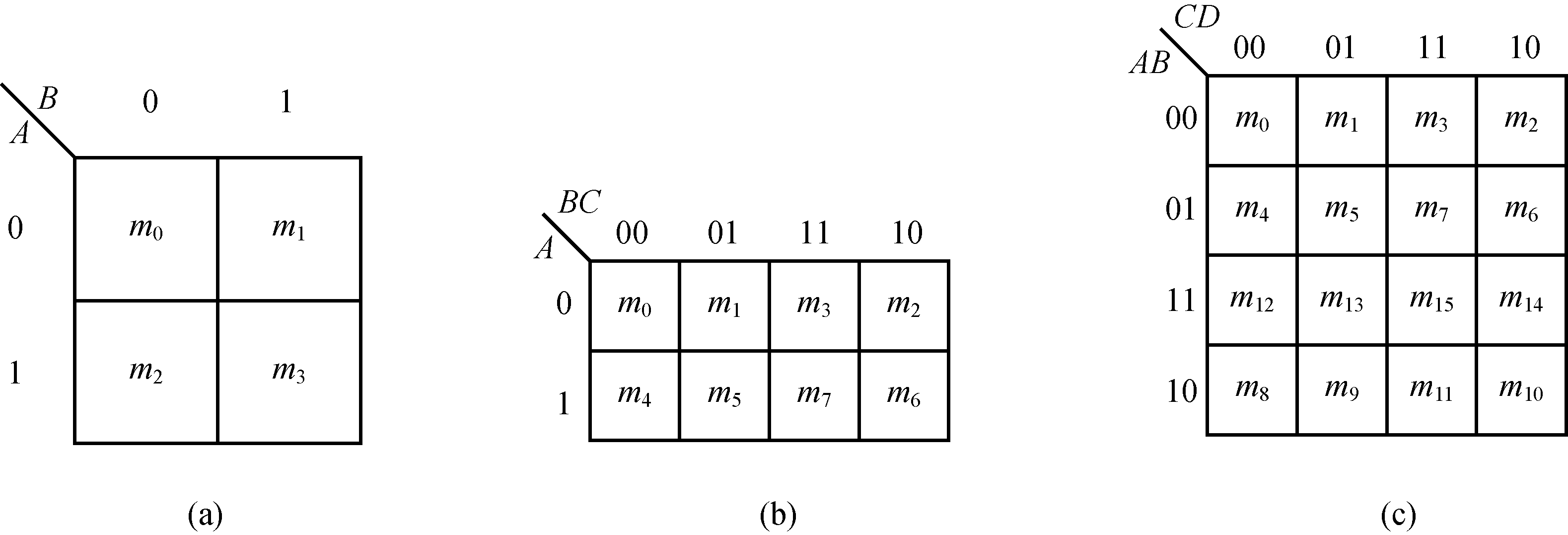
图9-13 二、三、四变量卡诺图

2.逻辑函数卡诺图

逻辑函数卡诺图的具体画法，通常有以下几种。

（1）给出逻辑函数的真值表

，根据真值表画出卡诺图。

（2）已知逻辑函数最小项表达式，由此画出函数的卡诺图。

（3）已知逻辑函数一般表达式，由此画出函数的卡诺图。

〖补充知识〗

逻辑函数的卡诺图化简法

1.最小项合并的规律

 

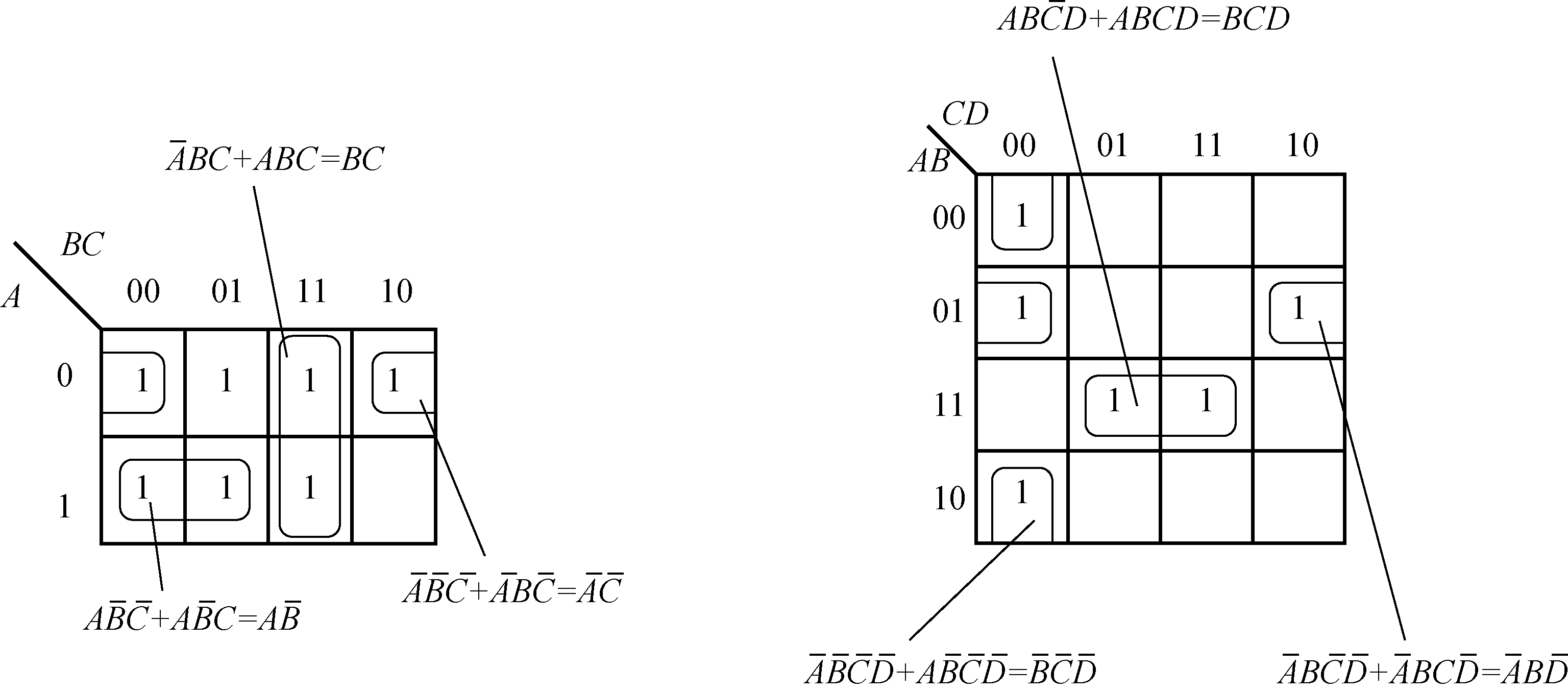
图9-17 两个相邻最小项的合并

2.用卡诺图法化简逻辑函数

卡诺图化简逻辑函数的一般步骤如下。

（1）根据变量数画出变量卡诺图。

（2）根据给出的要化简的逻辑函数，在函数包含的最小项方格中填1，其余的方格填0或不填，作出函数的卡诺图。

（3）合并相邻项，将能合并的最小项方格圈出。