第五节
上一节
下一节





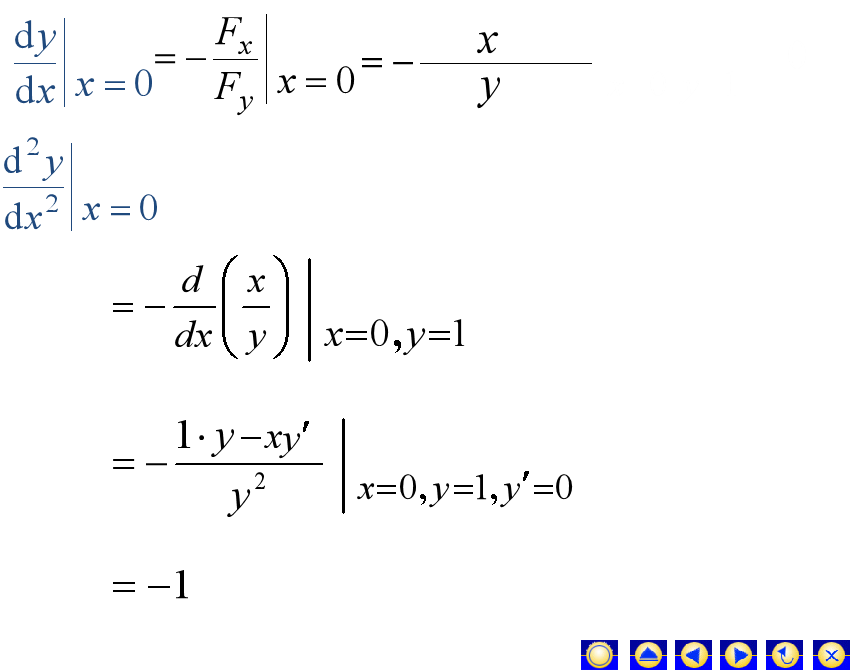

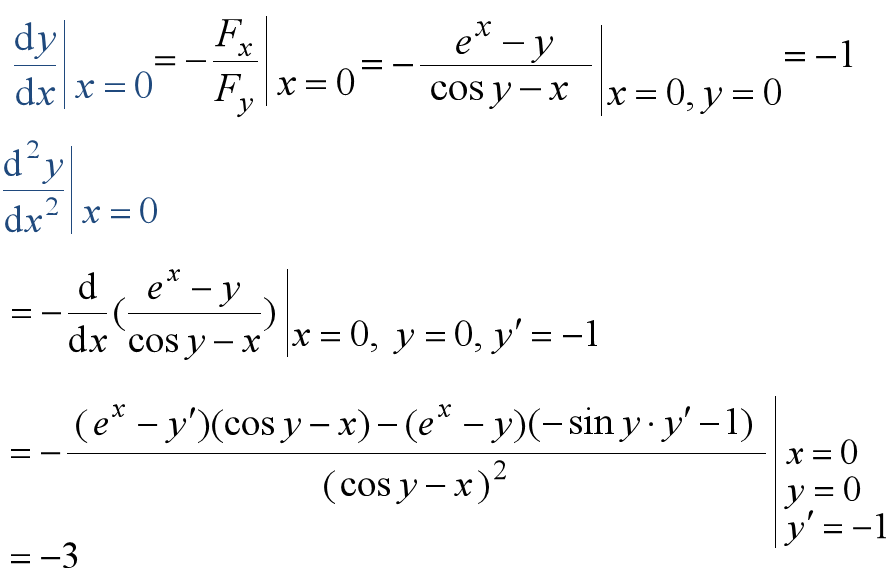







![]()









重点难点:
1.重点:利用全微分形式的不变性计算全微分、隐函数存在定理1、2、3;
2.难点:同上.
外语词汇:
derivative formula for implicit function
If is an implicit function of and defined by the equation ,then differentiation of both sides with respect to ,holding fixed,yields .If we solve for and note that ,we get the fist of the formulas below. A similar calculation holding fixed and differentiating with respect to produces the second formula
, .
复习思考题、课堂测试题、课外作业: 习题 9 --5 :1;2;3;4;5题.
复习思考题、课堂测试题、课外作业 :
习题 9 --5:6;7;8;9题;10(1)、(3);11.
推荐课外优秀教学视频:



