
授课题目:
第十一章 曲线积分与曲面积分
§1 对弧长的曲线积分
授课方式: 主讲+互动
教学目的与要求:
1.理解掌握对弧长的曲线积分的概念与性质;
2.理解掌握对弧长的曲线积分的计算法.






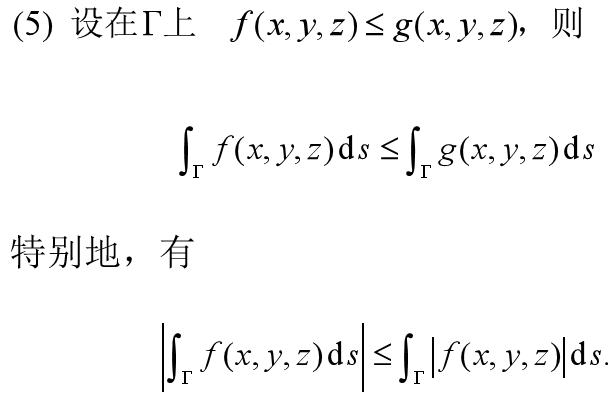















主 要 内 容 ( 按 教 学 大 纲 要 求 ):
§1 对弧长的曲线积分
一、对弧长的曲线积分的概念与性质
1.曲线形构件的质量
2.对弧长的曲线积分的定义
3.说明几点
4.对弧长的曲线积分的性质
二、对弧长的曲线积分的计算法
注意讲练结合
部分习题处理
总结知识要点布置作业
重点难点:
1.重点:对弧长的曲线积分的概念与性质、计算法;
2.难点:同上.
外语词汇:
Let C be a smooth plane curve,that is let C be given parametrically by ,where and are continuous and not simultaneously zero on .We say that C is positively oriented if its direction corresponds to increasing values of .We suppose that C is positively oriented and that C is traced only once as varies from to .Thus, C has initial point and terminal point .Consider the partition P of the parameter interval obtained by inserting the points This partition of results in a division of the curve C into subarcs in which the point corresponds to .Let denote the length of the arc ,and let be the longest length of the subarcs.Finally,choose a sample point on the subarc .Now consider the Riemann sum If this Riemann sum has a limit as .This limit is called the line integral of along C from A to B with respect to arc length; that is
复习思考题、课堂测试题、课外作业:
习题11--1 :1;2;3;4;5


