第三讲
上一节
下一节

授课题目:
第十一章 曲线积分与曲面积分
§2 对坐标的曲线积分 §3格林公式及其应用
授课方式: 主讲+互动
教学目的与要求:
1.理解掌握两类曲线积分之间的联系;
2.理解掌握格林公式.
主 要 内 容 ( 按 教 学 大 纲 要 求 ):
§2 对坐标的曲线积分
二、对坐标的曲线积分的计算法
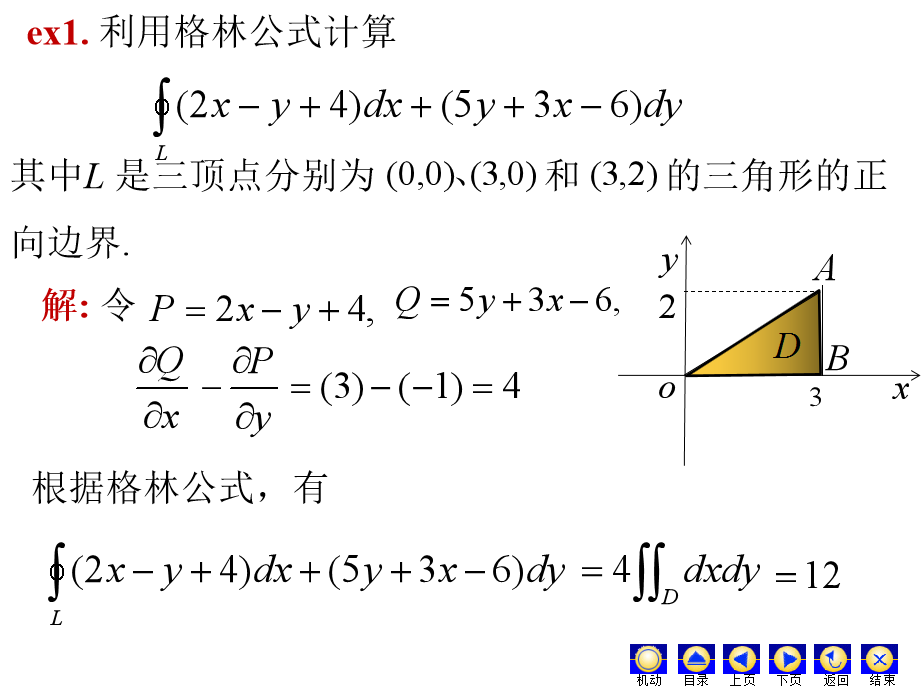
回忆(例题)
三、两类曲线积分之间的联系
§3 格林公式及其应用
(Green’sFormula and Its Applications)
一、格林公式
总结知识要点布置作业







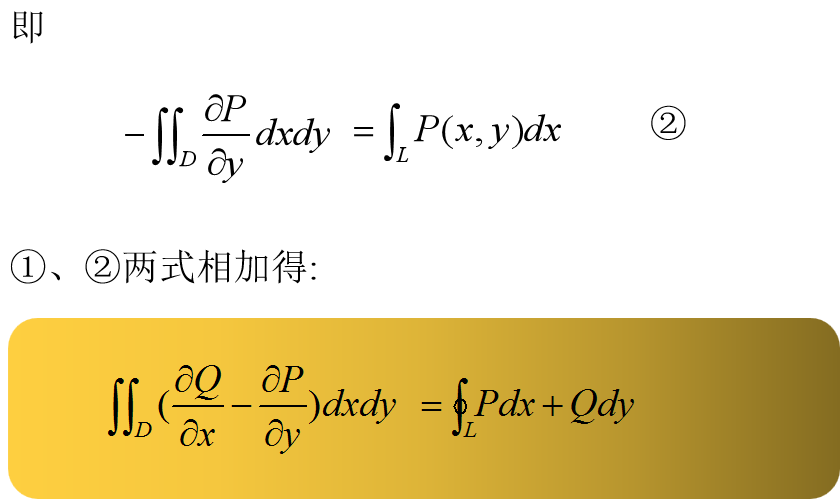







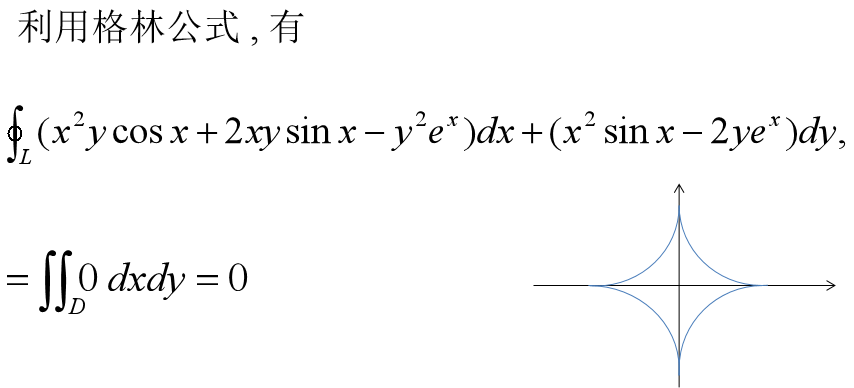




重点难点:
1.重点:格林公式;
2.难点:格林公式.
外语词汇:
Theorem1(Green’s Formula) Suppose C is a piecewise smooth simple closed curve bounding the domain D in the plane.Suppose and have continuous partial derivatives on D.Then
复习思考题、课堂测试题、课外作业:
习题11--:7;8;习题11--3 :1;2


