授课题目：

                第十章 重积分 

§1 二重积分的概念与性质  §2二重积分的计算法

授课方式： 主讲+互动

教学目的与要求：

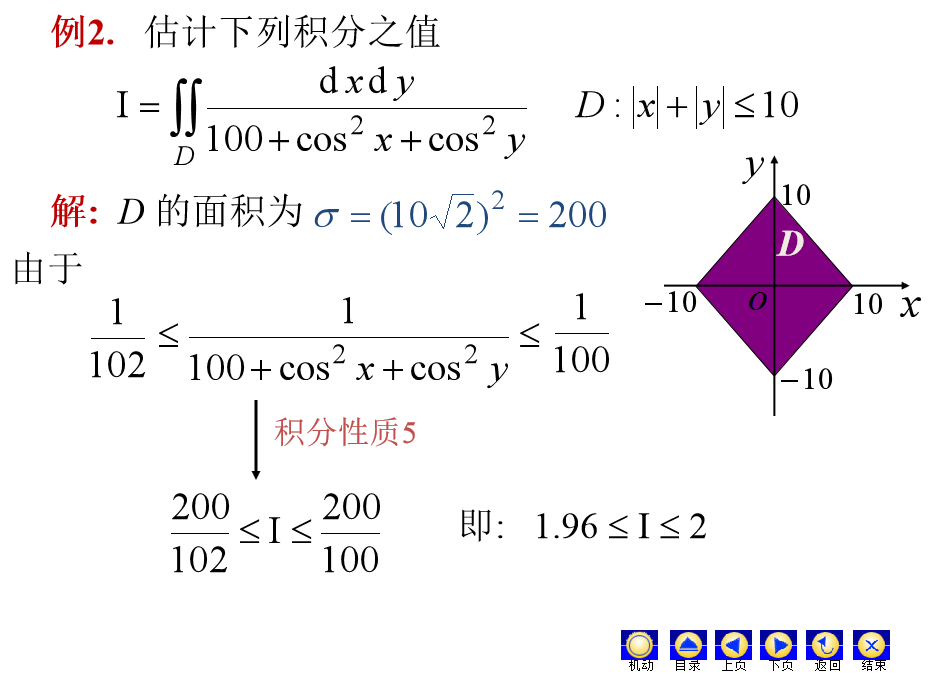
1．理解掌握二重积分的概念、性质；

2．理解掌握二重积分在直角坐标系下的计算.

主 要 内 容 ( 按 教 学 大 纲 要 求 ):

  §1 二重积分的概念与性质

一、二重积分的概念

1．曲顶柱体的体积

2．平面薄片的质量

3．二重积分的定义

4．说明几点

二、二重积分的性质

性质1，2，3，4，5，6

§2二重积分的计算法

一、利用直角坐标计算二重积分

总结知识要点布置作业                           

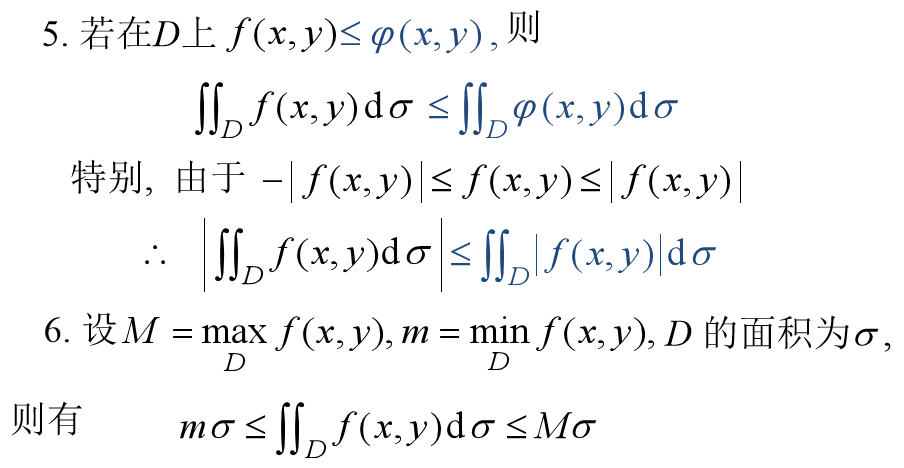
重点难点:

1.重点：二重积分的概念、性质、二重积分在直角坐标系下的计算；

2.难点：同上.

外语词汇:

Definition (The Double Integral) Let  be a bounded closed region in the   plane and   a function defined on  . Partition   arbitrarily into   subregions  ,whose area is denoted by  , Choose arbitrarily a point  in   and then form the sum  .Suppose that there exists a fixed number I such that for any  ,there exists a   such that if  the length  of the longest diameter of those subregions   in a partition of   is less than  ,then  ,no matter how the partition is and how those points   are chosen from  .Then   is said to be integrable over   and  I  is the double integral of over  ,written  , or 

复习思考题、课堂测试题、课外作业:

习题10—1  ：全做