授课题目： 第九章 多元函数微分法及其应用 

            §6 多元函数微分学的几何应用

授课方式： 主讲+互动

教学目的与要求：

1．掌握空间曲线的切线与法平面；

2．掌握空间曲面的切平面与法线的概念及求法.

主 要 内 容 ( 按 教 学 大 纲 要 求 )：

§6 多元函数微分学的几何应用

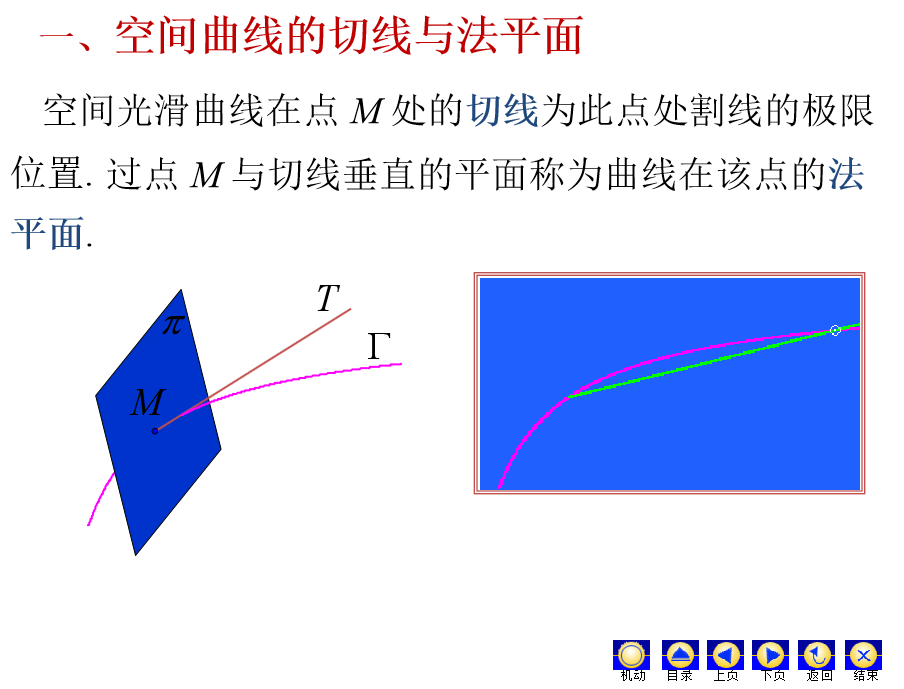
一、空间曲线的切线与法平面                        

  

1．空间曲线方程为参数方程形式  例1

  2．空间曲线方程为 形式

3．空间曲线方程为 形式   例2

二、曲面的切平面与法线                       

  

1．曲面方程为          形式

2．曲面方程为          形式                           

              例3、例4

三、习题练习

总结与布置作业                           

重点难点：

1.重点：空间曲线的切线与法平面；空间曲面的切平面与法线

2.难点：同上.

外语词汇：

Assume that the curve  is given by the parametric equations  , and functions   are differentiable on the interval  .Assume also that point   corresponds the value   of parameter  , then the equation of the tangent line to the curve   at point   is given by 

复习思考题、课堂测试题、课外作业： 习题 9 --6：1～10题.