·图象法的特点

直观形象、简化解题过程

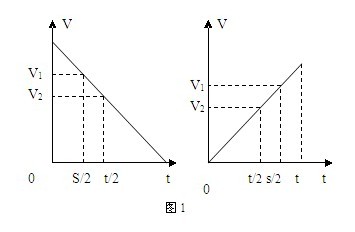
图象解法不仅思路清晰，而且直观、形象，可使解题过程得到简化。例如在比较匀速直线运动中的平均速度与中间位置的速度大小关系时，用图象法解题一目了然。如图1，平均速度即中间时刻速度，中间位置的瞬时速度即面积平分时刻的速度。依据图象能很快地得出结论

演示变化过程，让情景更直观

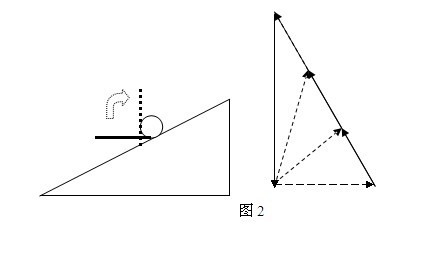
用图象法来描述物理过程则更直观，可以描述出其变化的动态特征，帮助学生理解物理过程。例如在分析用挡板挡住光滑斜面上的小球，分析挡板由水平位置转到竖直位置的过程中，小球对挡板与斜面的作用力如何变化时，可根据小球受三力作用平衡的条件：三力必构成一个封闭的矢量三角形。作动态分析图，如图2，由图示可得出两力的变化是：作用在挡板上的力先减小后增大，作用在斜面上的力一直在增大。

用于实验，简化数据处理

物理学习离不开物理实验，在物理实验中应用图象法进行数据处理，不仅具有简明、直观的特点，而且还可以减小误差、分析误差的成因。

·图象的物理意义

物理图象中“点”的物理意义

“点”是认识图象的基础。物理图象上的“点”代表某一物理状态，它包含着该物理状态的特征和特性。从“点”着手分析时应注意从以下几个特殊“点”入手分析其物理意义 。

⑴截距点。它反映了当一个物理量为零时，另一个物理的值是多少，也就是说明确表明了研究对象的一个状态。如图3中，图象与纵轴的交点反映出当I=0时，U＝E即电源的电动势；而图象与横轴的交点反映出电源的短路电流。

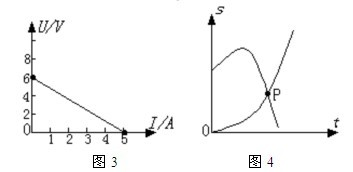
⑵交点。即图线与图线相交的点，它反映了两个不同的研究对象此时有相同的物理量。如图4中的P点表示甲、乙物体运动位移相同的时刻和位移。

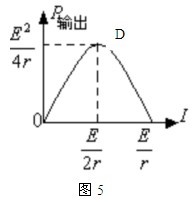
⑶极值点。它可表明该点附近物理量的变化趋势。如图5中的D点表明当电流等于E/(2r)时，电源有最大的输出功率。

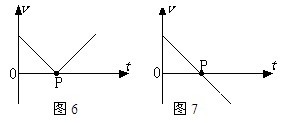
⑷拐点。通常反映出物理过程在该点发生突变，物理量由量变到质变的转折点。拐点分明拐点和暗拐点，对明拐点，学生能一眼看出其物理量发生了突变。如图6中的P点反映了加速度方向发生了变化而不是速度方向发生了变化。而暗拐点，学生往往察觉不到物理量的突变。如图7中P点看起来是一条直线，实际上在该点速度方向发生了变化。

物理图象中“线”的物理意义

主要指图象的直线或曲线的切线，其斜率通常具有明确的物理意义。

物理图象中“面”的物理意义

是指图线与坐标轴所围成的面积。如V-t图象面积表示位移，a-t图象面积表示速度变化量，F-t图象面积表示冲量，F-s图象面积表示功，i-t图象面积表示电量等等。

·图象应用的注意事项

1.必须搞清楚纵轴和横轴所代表的物理量，明确要描述的是哪两个物理量之间的关系。如辨析简谐运动和简谐波的图象，就是根据坐标轴所表示的物理量不同进行区别的。

2.要认识图线并不表示物体实际运动的轨迹。如匀速直线运动的S—ｔ图象是一条斜向上的直线，但物体实际运动的轨迹可能是水平的，并不是向上爬坡。

3.要从物理意义上去认识图象。由图象的形状应能看出物理过程的特征，特别要关注截距、斜率、图线所围面积、两图线交点等。很多情况下，写出物理量的解析式与图象进行对照，将有助于对图象物理意义的理解。