·认识不等式

1.如果a，b为正数，那么有：a+b≥2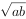，当且仅当a=b，取“=”号。

推论：

     ①两个正数的积一定时，两数相等时，其和最小。

     ②两个正数的和一定时，两数相等时，其积最大。

2.如果a，b，c为正数，则有a+b+c≥3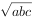，当且仅当a=b=c时，取“=”号。

推论：

     ①三个正数的积一定时，三数相等时，其和最小。

     ②三个正数的和一定时，三数相等时，其积最大。

·例题解析

例1.

一探险队员在探险时遇到一山沟，山沟的一侧竖直，另一侧的坡面呈抛物线形状。此队员从山沟的竖直一侧，以速度v₀沿水平方向跳向另一侧坡面。如图所示，以沟底的O点为原点建立坐标系Oxy。已知，山沟竖直一侧的高度为2h，坡面的抛物线方程为y＝x²；探险队员的质量为m。人视为质点，忽略空气阻力，重力加速度为g。

(1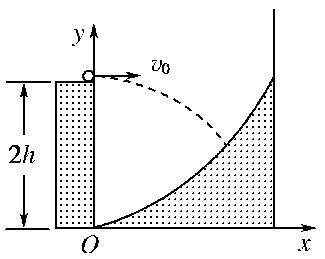)求此人落到坡面时的动能；

(2) 此人水平跳出的速度为多大时，他落在坡面时的动能最小？动能的最小值为多少？

 解析：(1)设该队员在空中运动的时间为t，在坡面上落点的横坐标为x，纵坐标为y.由运动学公式和已知条件得 

x＝v₀t①  

2h－y＝gt²②

根据题意有y＝③

由机械能守恒知落到坡面时的动能为mv²＝＋mg(2h－y)④

联立①②③④式得mv²＝m⑤

(2)⑤式可以改写为v²＝

显然v＋gh与之积为一恒量当，

即v₀＝时，其和最小。将v₀＝代入⑤得：_min＝mgh.

例2.

一轻绳一端固定在O点，另一端拴一小球，拉起小球使轻绳水平，然后无初速度的释放，如图所示，小球在运动至轻绳达到竖直位置的过程中，小球所受重力的瞬时功率在何处取得最大值？

解析：当小球运动到绳与竖直方向成θ角时，重力的功率为：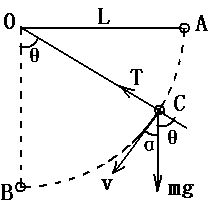                        

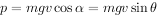
小球从水平位置到图中C点位置时，由机械能守恒：

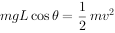
联立以上两式解得：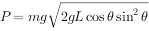

令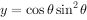,因为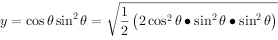

又因为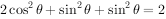 

根据基本不等式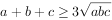定和求积知：

当且仅当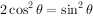即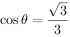时，y瞬时功率有最大值。

例3.

如图所示，一不可伸长的轻质细绳跨过滑轮后，两端分别悬挂质量为m₁和m₂的物体A和B，若滑轮有一定大小，质量为m且分布均匀，滑轮转动时与绳之间无相对滑动，不计滑轮与轴之间的磨擦，设细绳对A和B的拉力大小分别为T₁和T₂，已知下列四个关于T₁的表达式中有一个是正确的，请你根据所学的物理知识，通过一定的分析判断正确的表达式是（      ）

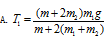
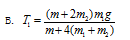
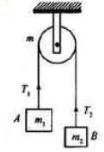
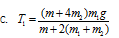
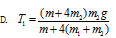
解析：

极值法1

令滑轮的质量m=0，则细绳对A和B的拉力大小T₁和T₂相等为T，假设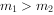，A和B一起运动的加速度为a，根据牛顿第二定律分别对A、B有：

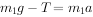
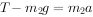
联立解得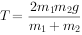：,分析判断可知C正确。

极值法2

令滑轮的质量m=0，且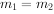，则T₁=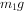，分析以上四个选项知C正确。