·认识二次函数

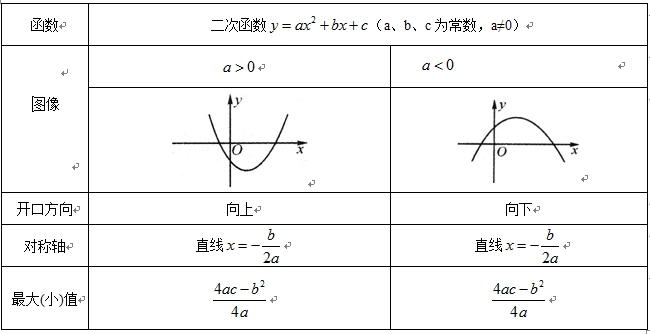
问题：对于二次函数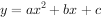(a≠0 )的图象及图象的形状、开口方向、位置又是怎样的？

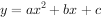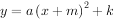          通过变形能将转化为的形式。

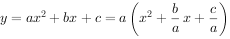
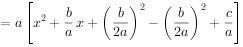
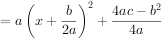
由此可见：当a>0时，则当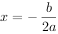时，y有最小值；

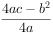           当a<0时，则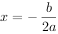时，y当有最大值。

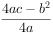二次函数的判别式

对于一元二次方程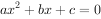，若判别式△≥0，则方程有实数解；△＜0，则方程无实数解。

·例题解析

例1.

一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以a＝3 m/s²的加速度开始行驶，恰在这一时刻一辆自行车以v自＝6 m/s的速度匀速驶来，从旁边超过汽车．试求：汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远？此时距离是多少？

解析：（法1）设汽车在追上自行车之前经t秒两车相距最远，则：

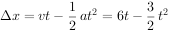
即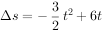

因为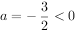，所以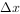应存在最大值；

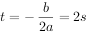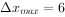当时，m。

即汽车追上自行车之前经过2s两车相距最远，最远距离为6m。

（法2）转化为一元二次方程：3t²-12t+2Δx=0

要使该方程有解，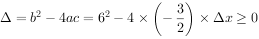

解不等式得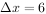m即两车最大相距6m。

将Δx=6m，代入方程，可得t=2s。

（法3）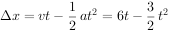

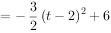
当t=2s时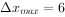，m