本章为一元函数积分学的推广，把定积分的知识推广到重积分，同时，重积分的运算又回到定积分，学生 从数学的角度体会，砥砺前行，不忘初心的情怀，通过本章知识的学习培养学生基本的创新思想和科学探索精 神，为后期部分专业课学习、论文的写作和竞赛等提供了准备平台。

      本章从实际例子的微元法求解出发，引入二重积分和三重积分的概念，不加证明地指出重积分存在的充分条件。对重积分的性质只加以叙述，省略证明。进而，重点介绍了重积分的经典计算方法及其拓展应用。重积分的计算最终都归结为定积分．学习中要抓住它与定积分之间的联系，注意比较它们的共同点与不同点．通过完成本章达标实训练习，可使读者达到以下要求。

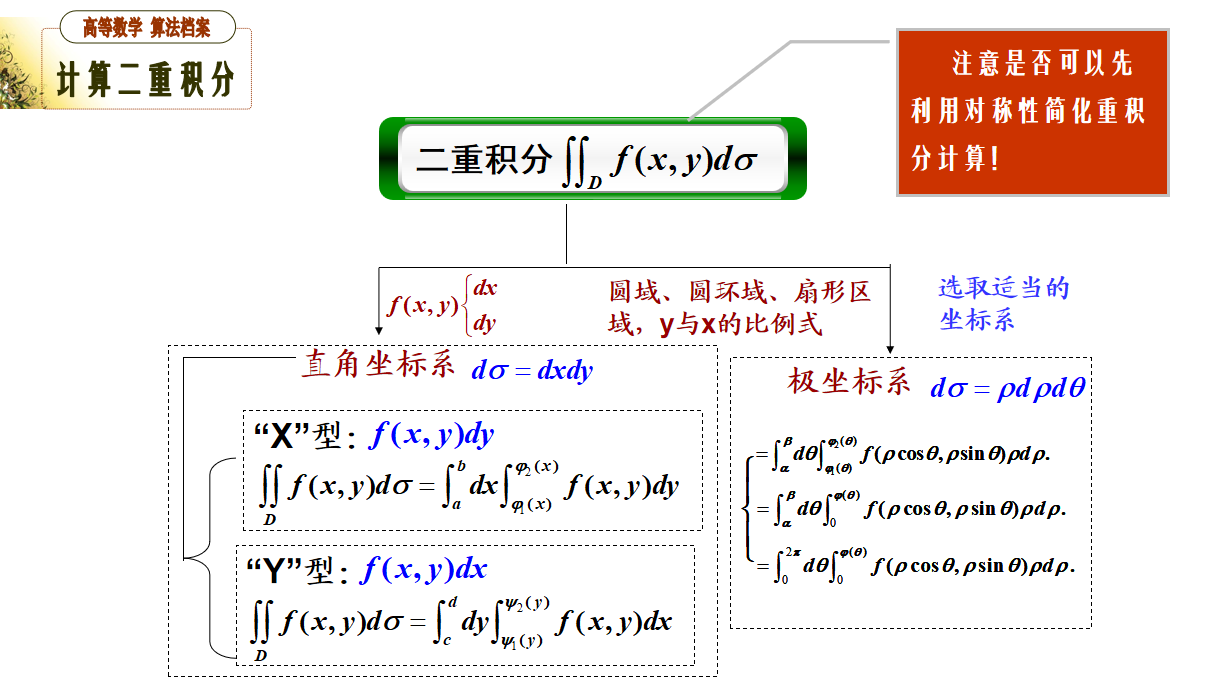
      一级达标要求：必须深刻理解重积分的概念和性质；学会利用对称性简化计算；掌握在不同坐标系下化重积分为累次积分的经典计算方法，包括利用直角坐标和极坐标计算二重积分的方法，利用直角坐标、柱面坐标计算三重积分的方法。

        在此基础之上，实现二级达标要求：会选择合适的坐标系和恰当的积分次序进行积分；掌握分段函数的二重积分方法；会利用极坐标计算一些特殊积分区域下的二重积分；会计算综合型的重积分问题及某些应用问题。

        最后，本章各节加入了达标自测题，同学们可以自我检测一下本阶段的学习成果。

牛顿：微积分的创始

怎么计算物体的运动？

      艾萨克·牛顿，17世纪和18世纪之交的英国数学家、物理学家和天文学家，对科学革命做出了巨大贡献。他发明的微积分是数学史上的一大里程碑，极大地推进了自然科学的发展。通过微积分，牛顿成功描述了自然界中的许多变化规律，包括经典力学的基石——牛顿运动定律和万有引力定律。

      牛顿的时代背景是科学革命的高潮期，这一时期欧洲科学家通过实验和数学推理揭示了自然界的许多基本原理。牛顿出生在英国林肯郡的一个小村庄。他在剑桥大学三一学院学习，在那里他开始对数学、物理和天文学产生浓厚兴趣。牛顿的学术生涯充满了创新，除了微积分的发明，他还在光学领域做出了重大发现，并通过他的著作《自然哲学的数学原理》系统地阐述了他的万有引力定律和三大运动定律。

      自然界的真理总是简单的。——牛顿

      牛顿研究微积分着重于从运动学来考虑，它提供了一种分析和描述变化率和累积量的方法。微积分主要由两个基本概念组成：微分和积分。微分学关注的是变化率，即函数在某一点处的瞬时变化速度；积分学则关注的是累积量，即一个量随另一个量变化的总和或总效应。牛顿的微积分理论使得科学家和工程师能够计算物体的速度和位置，分析光和声音的波动，以及优化各种系统的设计和功能。例如，考虑一个简单的物理问题：一个物体从静止开始自由下落的距离如何随时间变化。通过微分学，我们可以确定物体在任何给定时刻的速度（变化率），即速度是时间的函数。通过积分学，我们可以计算出物体在一段时间内下落的总距离（累积量）。这种分析方法不仅适用于物理学，还适用于经济学、生物学、工程学和许多其他领域的问题。

一、物理学中的应用

1. 质量计算：

• 在物理学中，二重积分常用于计算物体的质量。例如，对于一个密度不均匀分布的平面物体，可以通过二重积分来计算其总质量。

• 案例：计算一个金属板的质量，已知其密度函数ρ(x,y)在板上的分布。通过对密度函数在金属板所占区域D上进行二重积分，可以得到金属板的总质量。

2. 质心计算：

• 质心是物体质量的几何中心。对于密度不均匀分布的物体，质心的位置可以通过二重积分来计算。

• 案例：计算一个不规则形状物体的质心。首先，通过二重积分计算物体的总质量；然后，分别计算物体关于x轴和y轴的静矩，并通过静矩与总质量的比值来确定质心的坐标。

3. 转动惯量计算：

• 转动惯量是描述物体在转动时惯性大小的物理量。对于刚体，其转动惯量可以通过二重积分来计算。

• 案例：计算一个均匀半圆薄片关于其直径的转动惯量。通过设定合适的坐标系，将半圆薄片所占区域表示为x²+y²≤a²，y≥0，并应用二重积分公式来计算转动惯量。

二、工程学中的应用

1. 面积计算：

• 在工程学中，二重积分常用于计算复杂形状的面积。例如，可以通过二重积分来计算房屋内部或建筑物外部墙壁、窗户、屋顶等曲面的表面积。

• 案例：计算一个由复杂曲线围成的平面区域的面积。通过将区域分割成若干小块，并对每个小块上的面积进行二重积分求和，可以得到整个区域的面积。

2. 压力分布与总压力计算：

• 在力学分析中，二重积分可用于计算物体表面上的压力分布和总压力。例如，在流体力学中，可以通过二重积分来计算流体对物体表面的压力分布和总压力。

• 案例：计算一个平板在流体中的总压力。首先，确定流体对平板表面的压力分布函数；然后，通过二重积分计算平板表面的总压力。

3. 电场强度与电势能计算：

• 在电磁学中，二重积分可用于计算电场强度和电势能。例如，可以通过二重积分来计算电荷分布产生的电场强度和电势能。

• 案例：计算一个电荷分布产生的电场强度。首先，确定电荷分布函数；然后，通过二重积分计算电场强度分布。

三、经济学与社会学中的应用

1. 人口分布与密度分析：

• 在经济学和社会学中，二重积分可用于分析人口分布和密度。例如，可以通过二重积分来计算一个区域内的人口密度和总人口数。

• 案例：计算一个城市的人口密度分布和总人口数。首先，确定城市区域内的人口分布函数；然后，通过二重积分计算人口密度和总人口数。

2. 流量分布与概率密度函数：

• 在交通流量分析和概率论中，二重积分可用于计算流量分布和概率密度函数。例如，可以通过二重积分来计算交通流量在某一区域内的分布和总流量；或者计算某一随机变量的概率密度函数。

• 案例：计算一个交通路口的车流量分布。首先，确定车流量分布函数；然后，通过二重积分计算车流量在某一区域内的分布和总流量。

综上所述，二重积分在实验和应用中具有广泛的应用价值，可以用于计算物体的质量、质心、转动惯量等物理量；计算复杂形状的面积；分析压力分布与总压力；计算电场强度和电势能；以及分析人口分布、流量分布等经济学和社会学问题。

以下是二重积分实验应用案例的相关参考文献：

1. 《二重积分的计算与应用》：文章从二重积分相关的定义和定理、计算技巧、应用这三个方面来总结，介绍了二重积分在几何、力学、物理等方面的应用。

2. 《二重积分及其应用》：文章定义了矩形区域上的二重积分，并介绍了二重积分的应用，包括在开集上定义的二元函数的混合偏导数的连续性证明，以及使用二重积分证明级数求和公式等。

3. 《二重积分的应用》：文章摘要介绍了二重积分在工程设计，特别是建筑设计中的容积和表面积计算中的应用，以及如何通过数学建模和数学实践进行有机结合。

4. 《二重积分的应用实例》：文章通过实例详细说明了二重积分在求曲面面积、薄片重心和转动惯量等物理问题中的应用。

5. 《二重积分在数学、物理及实际生活中的应用论文》：文章通过实例说明了二重积分在数学、物理以及实际生活中的应用，包括在计算和证明、概率计算、积分不等式证明、几何和微分方程等方面的应用。

6. 《二重积分的对称性定理及其应用》：孙钦福在《科技信息》中介绍了二重积分的对称性定理，并给出了相关应用。

7. 《二重积分的对称性及其应用》：文章证明了二重积分的变量轮换对称性和奇偶对称性，并讨论了如何利用对称性简化二重积分的解题过程。

8. 《二重积分计算中“分部积分法”的应用》：文章主要讨论了在不交换积分次序的情况下如何利用分部积分法对二重积分进行计算。

9. 《二重数值积分方法及其在绝对节点坐标梁单元中的应用研究》：该文献探讨了二重数值积分方法在特定工程领域（如绝对节点坐标梁单元）中的应用。

10. 《二重积分的解法技巧及应用研究》：该文献可能包含对二重积分解法技巧的总结，以及这些技巧在不同领域中的应用案例研究。

这些参考文献涵盖了二重积分在不同领域的应用案例，包括数学、物理、工程设计和实际生活等，可以为研究和学习提供丰富的资料和参考。