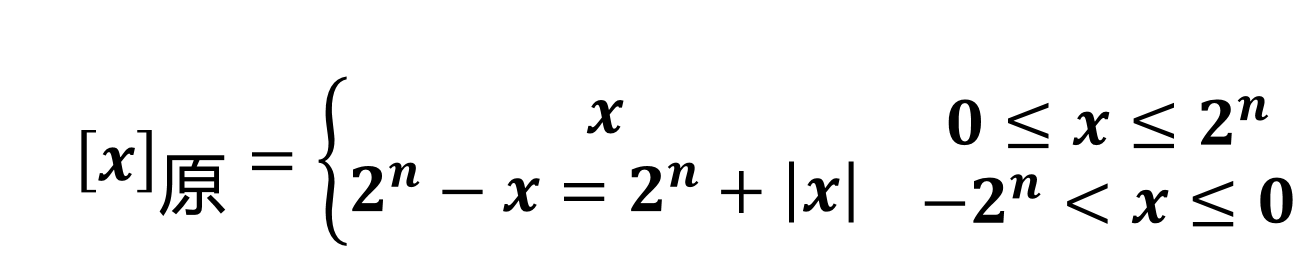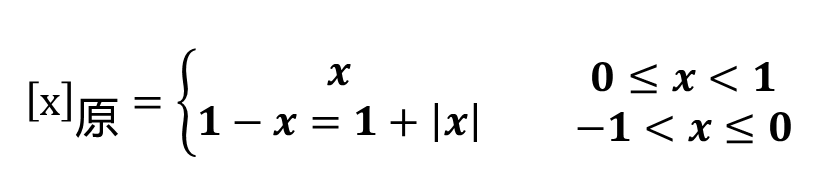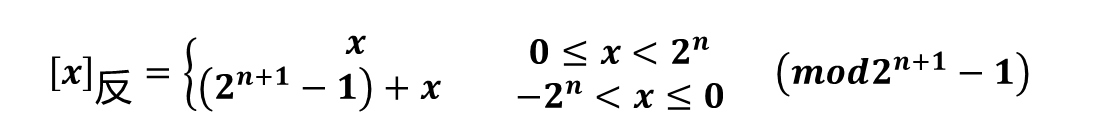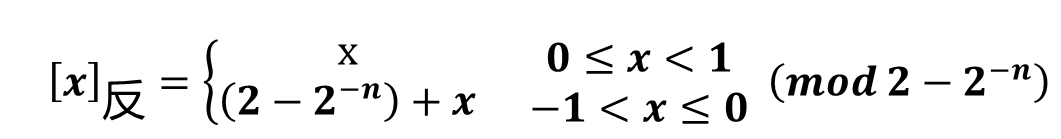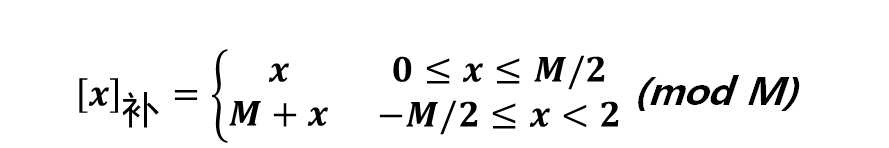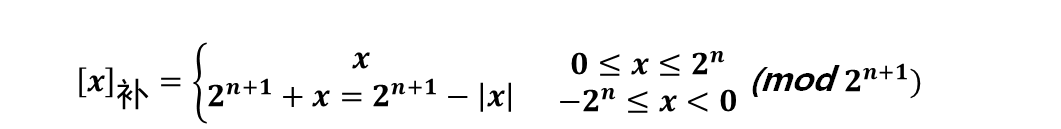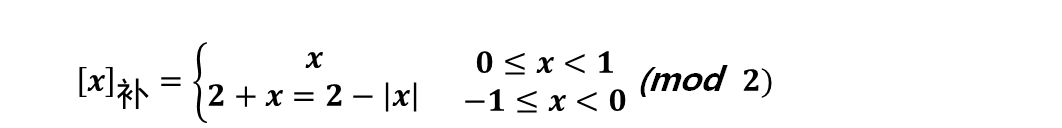数值数据的表示方法
编码
就是用少量简单的基本符号,选用一定的组合规则,以表示出大量复杂多样的信息。在计算机中,所有的数据都用二进制数来表示。任何数据都用二进制数进行编码。
数值数据是含有“量值”的数据,在计算机中分为无符号数和有符号数。按表示方法分为定点数据和浮点数据。 计算机中把符号位和数值位一起编码来表示相应的数,分别有原码、补码、反码和移码。
无符号数
所谓无符号数,顾名思义,就是没有符号的数,整个机器字长的全部二进制位均表示数值位(没有符号位),这种数相当于数的绝对值。(由于符号在页面上不好编辑,关于无符号数,请阅读以下文档)
有符号数
最高位被用来表示符号位,不再表示数值位。常用的表示方法:原码表示法、补码表示法、反码表示法、移码表示法。
对于有符号数来说, 符号的“+”“-”,机器是无法识别的, 但由于“正”“负”恰好是两种截然不同的状态, 如果用“0”表示“正”,用“1”表示“负”, 这样符号也就被数字化了。 如果规定将数字化的符号放在有效数字的前面, 就组成了有符号数。
数据的数值通常以正(+)负(-)号后跟绝对值来表示,称之为“真值”。
约定二进制数的最高位为符号位,0表示正号“+”,1表示符号“-”。这种在计算机中使用的表示数的形式称为机器数。
这种在计算机中使用的表示数的形式称为“机器数”。常见的机器数有“原码”、“反码”、“补码”等不同的表示形式。带符号数的最高位被用来表示符号位,而不再表示数值位。
为了区别一般书写表示的数和机器中这些编码表示的数,通常将前者称为真值,后者成为机器数或者机器码。
一旦符号数字化后, 符号和数值就形成了一种新的编码。
在运算过程中, 符号位能否和数值部分一起参加运算?如果参加运算, 符号位又需要做哪些处理?这些问题都和符号位与数值位所构成的编码有关,这些编码就是原码、补码、反码和移码。
也就是说, 常见的机器数有“原码”、“反码”、“补码”、“移码”等不同的表示形式。
数值数据的表示方法
原码
原码(Sign-Magnitude )是机器数中最简单的一种表示形式,符号位为0表示正数, 符号位为1表示负数, 数值位即真值的绝对值。
整数原码的定义:
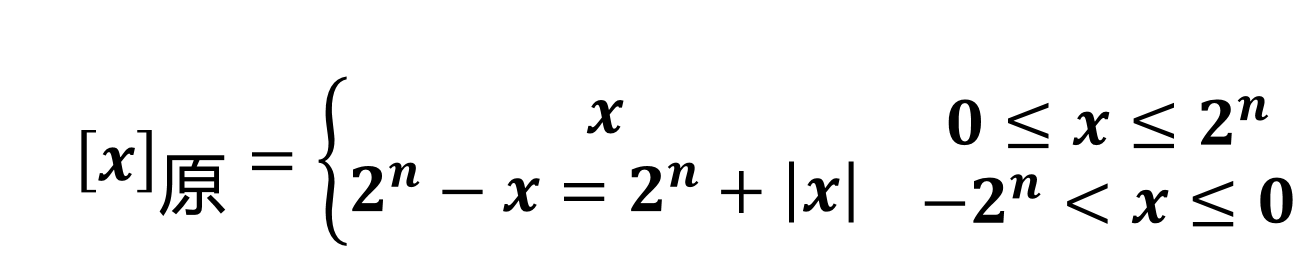
式中, x为真值, n为整数的位数
例如:
当x=+1110时, [x]原=01110
当x=−1110时, [x]原=24− (−1110)=11110
小数原码的定义:
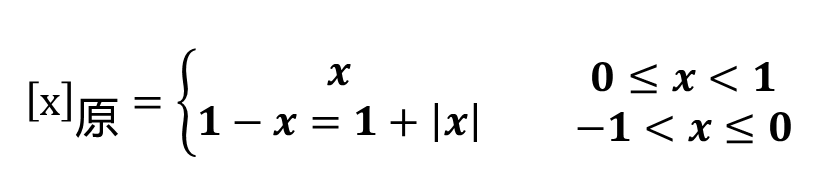
例如:
当x=+0.1101时, [x]原=0.1101
当x=−0.1101时, [x]原=1− (−0.1101)=1.1101
当x=0时,
[+0.0000]原=0.0000
[−0.0000]原=1−(0.0000)=1.0000
可见, [+0]原不等于[−0]原,即原码中的“零”有两种表示形式。
反码
反码通常是用来由原码求补码或者由补码求原码的中间过渡。
反码的编码原则是:由原码求反码,如果X为正数,则[X]反=[X]原;如果X为负数,则将[X]原除符号位以外,每位都变反,可得到[X]反。
整数反码的定义:
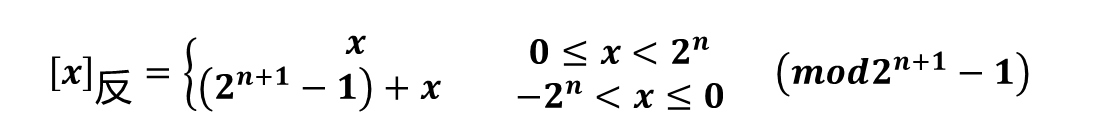
式中, x为真值, n为整数位数
当x=+1101时, [x]反=0 1101
当x=−1101时, [x]反=(x4+1−1)=11111−1101=1 0010
小数反码的定义:
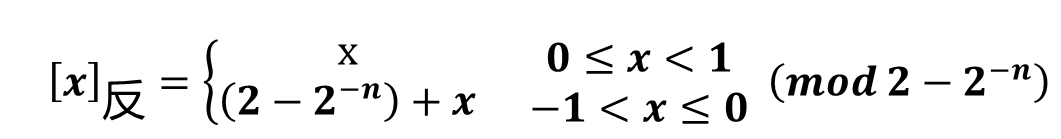
式中,x为真值, n为小数的位数
当x=+0.0110时, [x]反=0. 0110
当x=−0.0110时, [x]反=(2−2-4)+x=1.1111−0.0110=1. 1001
当x=0时,
[+0.0000]反=0.0000
[−0.0000]反=(10.0000−0.0001)−(0.0000)=1.1111
可见, [+0]原不等于[−0]原,即原码中的“零”有两种表示形式。
实际上,反码也可以看做是mod(2−2-n)(对于小数)或者mod(2n+1−1)(对于整数)的补码。
补码
首先,先来介绍两个概念,“模”和“同余”。
模(Module)是指一个计量器的容量。一般用M表示。是产生“溢出”的量值。
同余:用两个整数A和B除以同一个正整数M,如果所得的余数相同,则称A和B对M同余,即A和B在以M为模时是相等的,记作:
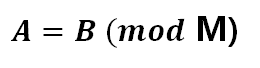
补码的定义:
任意一个X的补码为[X]补,可以用该数加上其模M来表示。
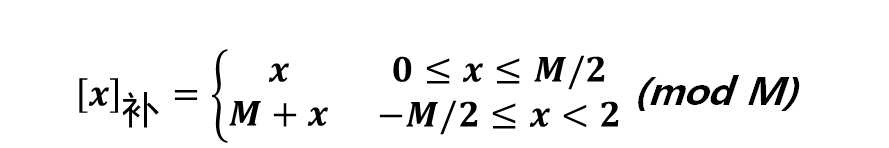
具体看整数补码的定义:
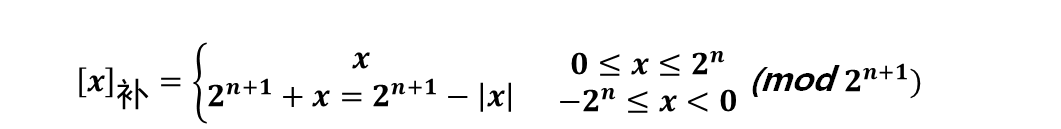
式中,x为真值, n为正数的位数
例如:
当x=+1010时,
[x]补=0 1010
当x=-1101时,
[x]补=2n+1+x=100000-1101=1 0011
再看小数补码的定义:
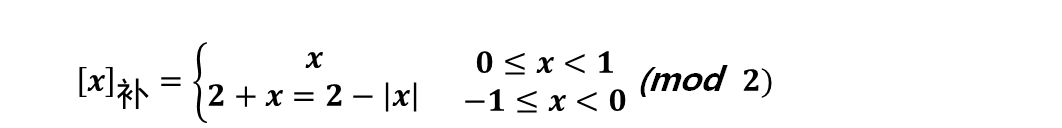
式中,x为真值
例如:
当x=0.1001时, [x]补=0.1001
当x=-0.0110时, [x]补=2+x=10.0000-0.0110=1.1010
当x=0时,
[+0.0000]补=0.0000
[-0.0000]补=2+(-0.0000)=10.0000-0.0000=0.0000
所以[+0]补=[-0]补=0.0000,即补码中的“零”只有一种表示形式。
对于小数,若x=-1, 根据小数补码定义,[x]补 =2+x=10.0000-1.0000=1.0000
由此可见, -1本不属于小数的范围,但是却有[-1]补存在。这是由于补码中的零只有一种表示形式,所以,它比原码能多表示一个-1 。所以补码的表示范围比原码多一个。
求补码的方法:
1. 由定义求补码:由真值求补码,直接利用补码的定义。反过来,由补码求真值,只需将公式左右进行交换就可以了。
2. 由原码求补码:正数的补码和原码相同,负数的补码,将原码除符号位以外的其余各位求反,末位加1。
对于负数,还有一个简便原则,可以将原码除符号位以外,其余各位按位取反,从最低位开始遇到的第一个1以前的各位保持不变。
扩展知识1——无符号数和有符号数的区别
无符号数就是整个机器字长的全部二进制位均表示数值位(没有符号位),相当于数的绝对值。
带符号数在日常生活中用“+”、“-”加绝对值来表示数值的大小,由于计算机无法识别“+”、“-”号,所以在计算机中需要将符号数码化。通常约定二进制数的最高位为符号位,0表示“+”,1表示“-”。带符号数在计算机中使用的表示数的形式为机器数, 常见的带符号机器数有原码、反码、补码等不同的形式。
数据由带符号数转换为同一长度的无符号数时,原来的符号位不再是符号位,而成为数据的一部分,所以负数转换成无符号数时,数值将发生改变。数据由无符号数转换为同一长度的带符号数时,各个二进制位的状态不变,但最高位被当做符号位,这时也会发生数值改变。
扩展知识2——C语言中的有符号数与无符号数
C语言支持所有整型数据类型的有符号和无符号运算。 几乎所有的机器都使用补码。通常,大多数数据都默认为是有符号的。
C语言允许无符号数和有符号数之间的转换。
虽然C标准没有精确规定应如何进行这种转换, 但大多数系统遵循的原则是底层的位保持不变。由于C语言对同时包含有符号和无符号表达式的这种处理方式, 出现了一些奇特的行为 。当执行一个运算时, 如果它的一个运算数是有符号的而另一个是无符号的, 那么C语言会隐式地将有符号数强制转换为无符号数, 并假设这两个数都是非负的, 来执行这个运算。
关键词(key-word)
数值数据:numerical data
编码:code
解码:decode
无符号数:Unsigned Data
有符号数:Signed Data
符号位:sign bit
原码:Sign-Magnitude
补码: Complement code
1的补码(反码)表示法:ones complement representation
移码表示法:biased representation