定点数的表示
定点数:
定点数就是小数点固定在某一个位置上的数。它只是一种隐含的约定,并没有一个器件的用来专门存放小数点。
对于一个n+1位的二进制数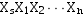 来说,这里Xs是它的符号位,X1是它的最高数值位,Xn是它的最低数值位。那么如果说我们把小数点的位置约定在最符号位和最高数值位之间,我们就把它称为是一个定点的纯小数,如果我们约定小数点在最低数值位之后,就称为定点的纯整数。
来说,这里Xs是它的符号位,X1是它的最高数值位,Xn是它的最低数值位。那么如果说我们把小数点的位置约定在最符号位和最高数值位之间,我们就把它称为是一个定点的纯小数,如果我们约定小数点在最低数值位之后,就称为定点的纯整数。
采用定点数的机器呢,我们把它称为是定点机。
定点数的表示范围
对于n+1位的定点小数机, 所能表示的范围是:
对于正数, 无论是原码还是补码, 所能表示的范围是一样的。
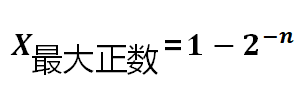

对于负数, 如果是原码:

如果是补码:

对于n+1位定点整数机,所能表示的范围是:
对于正数, 无论是原码还是补码, 所能表示的范围是一样的。
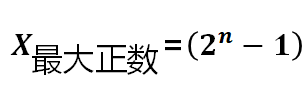

对于负数, 如果是原码:

如果是补码:

溢出
参加运算的数以及运算的结果都必须保证落在该定点机所能表示的数值范围内,如果结果大于最大正数或者小于绝对值最大的负数,称为“溢出”。
浮点数的表示
浮点数
顾名思义就是小数点不固定的数。
对于一个二进制的数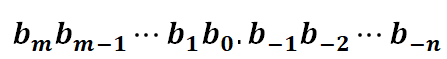 ,其中每个bi的取值范围那只有0和1,可以表示为:
,其中每个bi的取值范围那只有0和1,可以表示为:
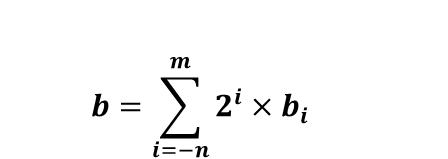
小数点左边的数值的权位是2的正幂,得到的是整数值,而小数点右边的权是2的负幂,得到的是小数值。
一个任意进制的数,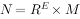
其中,R称为是基数通常可取值2,8,16等;M称为尾数(Mantissa)是一个纯小数,它包含了数N的全部有效数字;E称为阶码(Exponent)是一个纯整数。它指出了小数点在数N中的位置。由于这里的阶码可以取不同的数值,所以说小数点的位置是不固定的。这就是浮点数的由来。
在计算机中由于基数是在系统中隐含约定的不需要专门表示,因此在进行浮点数编码的时只需要用一对定点数分别表示阶码e和尾数M就可以了。浮点数的格式如图所示,其中用定点整数表示阶码,它的大小反映了小数点在数N中的实际位置。尾数M用定点小数表示,它的符号位决定整个数N的正负即为数N的符号位,尾数的大小决定了数N的精度。由此,可以看出浮点数的表示范围主要由阶码的位数来确定,而有效数字的精度主要由尾数的位数决定。
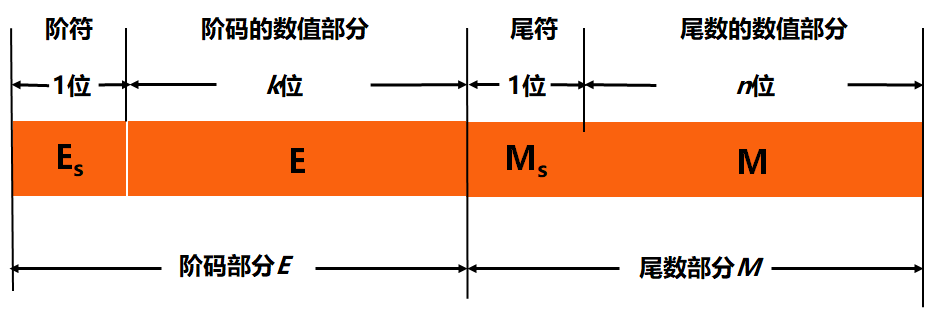
浮点数的表示范围
在给定存储位数的情况下,浮点数的表示范围也是有限的。
假设尾数和阶码均用补码表示,阶码的位数位k位,尾数的位数为n位,
最大的正数:当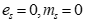 ,阶码和尾数的数值位各位全为1时,该浮点数为最大的正数,即:
,阶码和尾数的数值位各位全为1时,该浮点数为最大的正数,即:
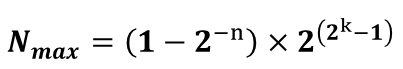
最小的正数:当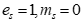 ,尾数的最低位为1,其余各位为0,阶码为绝对值最大的负数,尾数为最小正数时,该浮点数为最小的正数,即:
,尾数的最低位为1,其余各位为0,阶码为绝对值最大的负数,尾数为最小正数时,该浮点数为最小的正数,即:
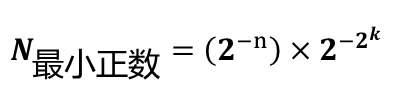
绝对值最小的负数:当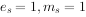 ,尾数的最低位为1,其余各位为1,阶码为绝对值最大的负数,尾数为最小正数时,该浮点数为绝对值最小的负数,即
,尾数的最低位为1,其余各位为1,阶码为绝对值最大的负数,尾数为最小正数时,该浮点数为绝对值最小的负数,即

绝对值最大的负数:当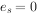 ,阶码的数值为全1,当
,阶码的数值为全1,当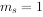 ,尾数的数值位为全0,即阶码为最大正数,尾数为绝对值最大的负数时,该浮点数为绝对值最大负数,即:
,尾数的数值位为全0,即阶码为最大正数,尾数为绝对值最大的负数时,该浮点数为绝对值最大负数,即:

规格化数
由于一个浮点数的表示形式并不是唯一的。为了便于数据的比较和运算,需要像十进制数的科学计数法一样,在二进制数中,用规格化浮点数表示。
规格化浮点数的定义:尾数M的绝对值满足下列条件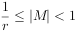 的数称为规格化的浮点数。简单地说,对于二进制数来说,所谓规格化的浮点数数就是尾数M的绝对值应大于或等于0.5。
的数称为规格化的浮点数。简单地说,对于二进制数来说,所谓规格化的浮点数数就是尾数M的绝对值应大于或等于0.5。
规格化数的判别方法:
当尾数用原码表示时,尾数满足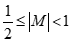 ,0.1****和1.1****,即尾数的最高数值位一定为1.
,0.1****和1.1****,即尾数的最高数值位一定为1.
当尾数用补码表示时,尾数的最高数值位和符号位相反。当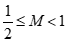 , 应有形式
, 应有形式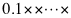 ;当
;当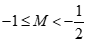 时,应有
时,应有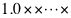 形式。
形式。
特别说明:当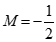 时,对于原码来说是一个规格化数,但是对于补码来说,它不是一个规格化数。当
时,对于原码来说是一个规格化数,但是对于补码来说,它不是一个规格化数。当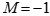 时,对于原码来说,是无法表示的。但对于补码来说,是一个规格化数。
时,对于原码来说,是无法表示的。但对于补码来说,是一个规格化数。
对于非规格化浮点数需要进行规格化操作才能变成规格化浮点数。所谓规格化操作就是通过相应地调整一个非规格化浮点数的尾数和阶码的大小,使非零的浮点数在尾数的最高位上保证是一个有效值。
IEEE754标准的浮点数
在计算机中通常采用IEEE754标准的浮点数,IEEE754标准是电气和电子工程师协会(IEEE)于1985年推出。
IEEE浮点数标准用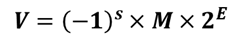 形式来表示一个数。
形式来表示一个数。
符号(sign):s决定这数是负数(s=1)还是正数(s=0),对于数值0的符号位解释作为特殊情况处理
尾数(significand):M是一个二进制小数
阶码(exponent):是对浮点数加权,这个权重是2的E次幂
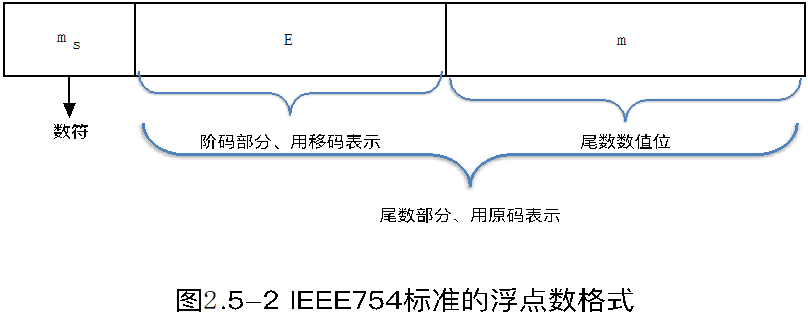
IEEE754标准中的浮点数有3种分别为:单精度浮点数、双精度浮点数和扩展精度浮点数。其中单精度浮点数和双精度浮点数均采用隐含尾数最高数位的方法。扩展精度浮点数没有隐含位。
表 IEEE754 标准中的3种浮点数
| 类型 | 数符 | 阶码 | 尾数数值 | 总位数 | 偏置量 |
| 十六进数 | 十进制 |
| 短浮点数 | 1 | 8 | 23 | 32 | 7FH | 127 |
| 长浮点数 | 1 | 11 | 52 | 64 | 3FFH | 1023 |
| 临时浮点数 | 1 | 15 | 64 | 80 | 3FFFH | 16383 |
在32位的单精度浮点数中,最高位是数符位,其后是8位的阶码,阶码用移码表示,其余的23位是尾数位。在单精度浮点数中有一位隐含位,由于规格化浮点数的数值最高位始终为1,所以可以将这一位隐含,因此尾数的数值位实际上为24位。
特别说明:隐含的1是一位整数(即位权为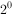 )。在浮点格式中表示出来的23位尾数是纯小数,用原码表示。
)。在浮点格式中表示出来的23位尾数是纯小数,用原码表示。
定点、浮点表示法的区别
(1) 数值的表示范围:
如果定点数和浮点数的位数相同,那么浮点表示法所能表示的数值范围将远远大于定点表示法。浮点数的阶码部分的位数越多,可表示的数值范围越大。
(2) 精度:
精度是指一个数所能包含的有效数值位的位数。一般来说,机器字长越长,所能表示的数的有效位数就越多,精度就越高。对于位数相同的定点数和浮点数,浮点数扩大了数的表示范围,但是是以降低精度为代价。
(3) 数的运算:
浮点数包括阶码和尾数两部分,运算时需要对尾数和阶码分别计算。而且运算结果都要规格化。
(4) 溢出处理:
在定点数运算时,当运算结果超出数的表示范围时,就发生溢出;在浮点运算时,运算结果超出尾数的表示范围不一定溢出,只有当阶码超出所能表示的范围时,才发生溢出。
关键词
定点数:fixed-point number
浮点数:floating-point number
IEEE: Institute of Electrical and Electronics Engineers

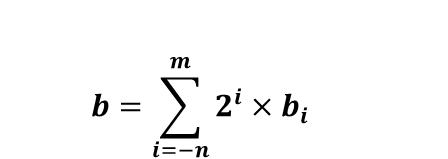

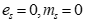
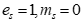
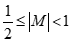 ,0.1****和1.1****,即尾数的最高数值位一定为1.
,0.1****和1.1****,即尾数的最高数值位一定为1.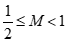 , 应有形式
, 应有形式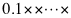 ;当
;当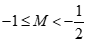 时,应有
时,应有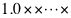 形式。
形式。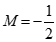 时,对于原码来说是一个规格化数,但是对于补码来说,它不是一个规格化数。当
时,对于原码来说是一个规格化数,但是对于补码来说,它不是一个规格化数。当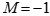 时,对于原码来说,是无法表示的。但对于补码来说,是一个规格化数。
时,对于原码来说,是无法表示的。但对于补码来说,是一个规格化数。

