浮点数加减运算
设有两个规格化浮点数的分别为:
X=Mx*2Ex,
Y=My*2Ey,
加减法运算通式为:
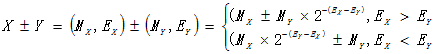
执行浮点数的加减运算,需要经过对阶、尾数加/减、尾数结果规格化、舍入、判溢出等步骤。
⑴.0操作数检查:用来判断两个操作数中是否有一个为0.
⑵.对阶操作:即比较两个浮点数的阶码值的大小,求E=Ex-Ey,然后将小阶对大阶。
⑶.尾数进行加或减运算:实现尾数的加减运算
,执行两个完成对阶后的浮点数的求和(差)的过程。
⑷.规格化并进行舍入处理:若得到的结果不满足规格化规则,就必须把它变成规格化的数。舍入操作,在执行对阶或右规操作时,会使位数低位上的一位或若干位的数值被移掉,使数值精度受到影响,可以把移掉的几个高位的值保存起来供舍入使用。
对阶
两个浮点数相加或相减,首先要把小数点的位置对齐,而浮点数的小数点的实际位置取决于阶码的大小,因此,对齐两数的小数点,就是使两数的阶码相等,这个过程称为对阶。
首先计算两数阶码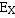 和
和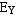 之差,即:
之差,即:
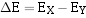
若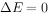 ,表示两数阶码相等,即
,表示两数阶码相等,即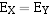 ;
;
若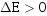 ,表示
,表示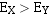
若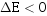 ,表示
,表示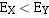
当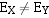 时, 要通过尾数的移位来改变
时, 要通过尾数的移位来改变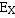 或
或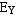 ,使
,使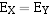 相等。
相等。
对阶的规则是:小阶向大阶对齐。即阶码小的数的尾数右移,每右移一位,阶码加1,知道两数的阶码相等为止。
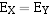 ,无需对阶。
,无需对阶。
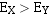 ,则
,则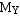 右移。每右移一位,
右移。每右移一位,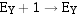 ,直至
,直至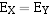 为止。
为止。
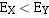 ,则
,则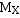 右移。 每右移一位,
右移。 每右移一位,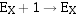 ,直至
,直至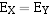 为止。
为止。
尾数右移后,应对尾数进行舍入。
尾数加/减
对阶之后,就可以进行尾数加/减,即:
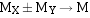
算法与前面介绍的的定点数的加/减法相同。
尾数结果规格化
尾数加/减运算之后得到的数可能不是规格化数 ,为了增加有效数字的位数,提高运算精度,必须进行结果规格化操作。
假设尾数用补码表示,如果尾数结果的符号位与最高符号数值位相同,需要使尾数左移以实现规格化,这个过程称为左规。尾数每左移一位,阶码相应减1(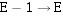 ),直至成为规格化数为止。
),直至成为规格化数为止。
若在尾数加/减运算中出现溢出,在浮点运算中,只能表明此时尾数的绝对值大于1,而非真正的溢出。这种情况应将尾数右移以实现规格化。这个过程称为右规。尾数每右移一位,阶码相应加1(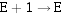 )。右规最多只有一次。
)。右规最多只有一次。
舍入
通常有三种方法:恒舍法、0舍1入法、恒置1法。
溢出判断
与定点加减法一样,浮点加减运算最后一步也需要判溢出。浮点数的溢出情况是由阶码的溢出决定。
算法流程图
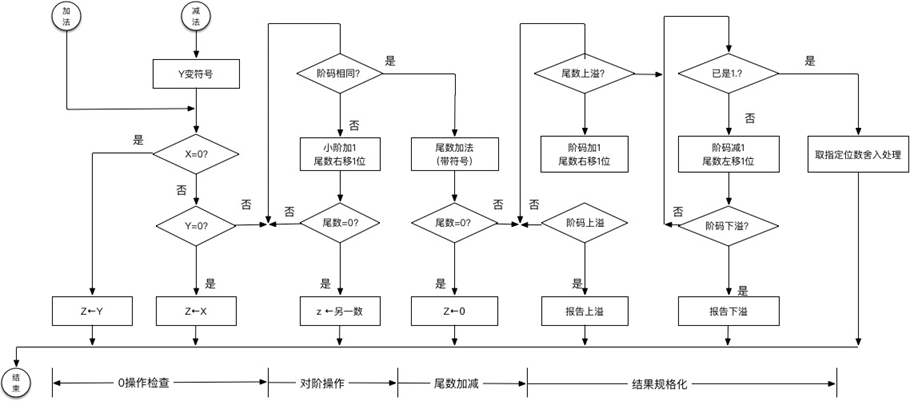
浮点乘除运算
设两个非0的规格化浮点数分别为:
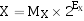
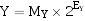
规格化浮点数X、Y乘除运算通式为:
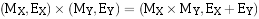
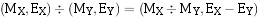
乘法步骤
两浮点数相乘,其乘积的阶码应为相乘两数的阶码之和,其乘积的尾数应为相乘两数的尾数之积。即:
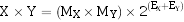
(1)阶码相加
如果阶码用补码表示,阶码相加之后无须校正;当阶码用偏置值为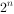 的移码表示时,阶码相加后要减去一个偏移量
的移码表示时,阶码相加后要减去一个偏移量 。
。
如果阶码相加后产生溢出,应另做处理。
(2)尾数相乘
若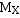 、
、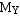 都不为0,则可进行尾数乘法。尾数乘法的算法与前述定点数乘法算法相同。
都不为0,则可进行尾数乘法。尾数乘法的算法与前述定点数乘法算法相同。
(3)尾数结果规格化
由于X、Y均是规格化数,所以尾数相乘后的结果一定落在下列范围内:
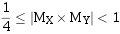
当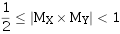 时,乘积已是规格化数,无须再进行规格化操作;
时,乘积已是规格化数,无须再进行规格化操作;
当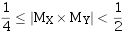 时,则需要左规一次。左规时调整阶码后如果发生阶码下溢,则做机器零处理。
时,则需要左规一次。左规时调整阶码后如果发生阶码下溢,则做机器零处理。
除法步骤
两浮点数相除,其商的阶码应为相除两数的阶码之差,其商的尾数应为相除两数的尾数之商。即:
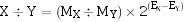
(1)尾数调整
为了保证商的尾数是一个定点小数,首先需要检测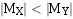 。如果不小于,则
。如果不小于,则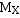 右移一位,
右移一位,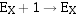 ,称为尾数调整。因为X、Y都是规格化数,所以最多调整一次。
,称为尾数调整。因为X、Y都是规格化数,所以最多调整一次。
(2)阶码相减
如果阶码永不吗表示,阶码相减以后无须校正;当阶码用偏置值为 的移码表示时,阶码相减后要加上一个偏移量
的移码表示时,阶码相减后要加上一个偏移量 。阶码相减后,如有溢出,应另作处理。
。阶码相减后,如有溢出,应另作处理。
(3)尾数相除
若 、
、 都不为0,则可进行尾数除法。尾数除法的算法与前述定点数除法算法相同。因为开始时已进行了尾数调整,所以运算结果一定落在规格化范围内。即:
都不为0,则可进行尾数除法。尾数除法的算法与前述定点数除法算法相同。因为开始时已进行了尾数调整,所以运算结果一定落在规格化范围内。即:
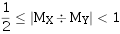
浮点运算部件
浮点运算部件通常由阶码运算部件和尾数运算部件组成,其各自的结构与定点运算部件相似,但阶码部分仅执行加减法运算。其尾数部分则执行加减乘除运算,左规时有时需要左移多位。
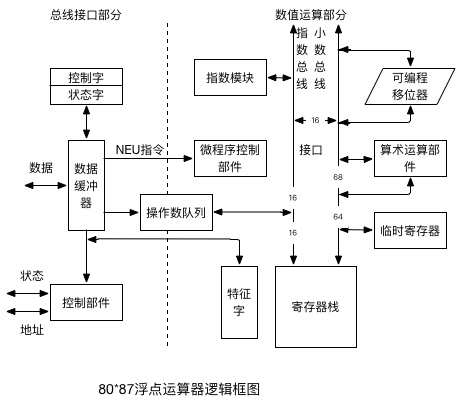
图3.7-1 80*87浮点运算器逻辑框图
关键词(keyword)
浮点表示法:floating-point representation
规格化数:normalized number
非规格化数:denormalized number
指数(阶值)exponent
阶值上溢:exponent overflow
阶值下溢:exponent underflow