选择两个素数p，q（不要告诉别人），假设是p=2，q=5，算出n=p×q= （1） ，将n公开。

计算n的欧拉函数Φ(n) = (p-1) ×(q-1)= （2） 。从1到Φ(n)之间选择一个和Φ(n)互素的数e公开，这里选择e = （3） 。

计算解密密钥d，使得(d×e) modΦ(n) = 1，这里可以得到d= （4） 。

将n = （1） 和e = （3）公开；将d = （4）保密。这样就可以加密和解密了。

例如，要发送的信息为s=2，那么可以通过如下计算得到密文：

                        c = se mod (n) =  （5） 。

密文8可以使用d = 3恢复出明文：

                       s = cd mod (n) =  （6） 。

只要知道素数和互素概念的小学生都能很快给出答案：（1）10；（2）4；（3）3；（4）3；（5）8；（6）2。 

如果给定两素数，不用通过人工计算或编程得到，我们用RSA-Tool工具就可以很容易得到公钥n和e，以及私钥d。

如假设两个素数p=101，q=113。下面通过一个小工具RSA-Tool演示上面所说的过程。

如下图所示，选择好密钥长度（Keysize）和进制（Number Base），并确定P、Q和公钥E（Public Exponent）的值后，单击按钮，则可算出N和私钥D。

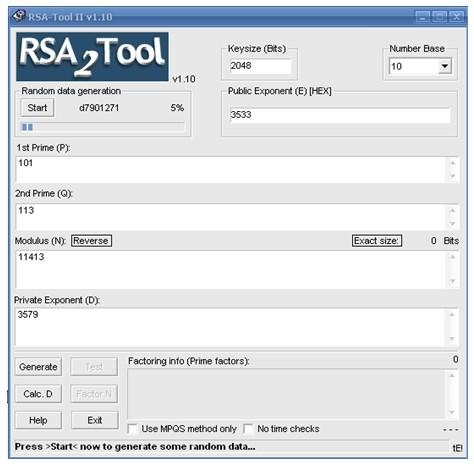
从图可知，公开加密密钥（n，e）=（11413，3533）。解密密钥d=3579。这样就可以使用公钥对发送的信息进行加密，接收者如果拥有私钥，就可以对信息进行解密了。例如，要发送的信息为s=9726，那么可以通过如下计算得到密文：

c = se mod (n) 

= 97263533 mod (11413) 

= 5761。

将密文5761通过信道发送给接收端，接收者在接收到密文信息后，可以使用私钥d = 3579恢复出明文：

s = 57613579 mod (n) 

=57613579 mod (11413) 

= 9726。 

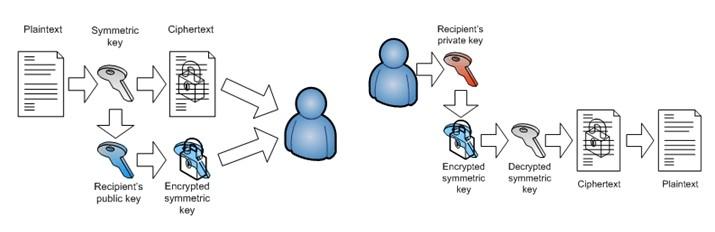
混合加密过程

 对截取的密报依次用各种可解的密钥试译，直到得到有意义的明文；或在不变密钥下，对所有可能的明文加密直到得到与截获密报一致为止。此法又称为穷举破译法（Exhaustive decoding method）或完全试凑法（Complete Trial-and-error Method）或暴力破解法。

      例 移位密码分析

            密文：BJQHTRJYTXMFSLMFNJCUT

            方法：依次尝试所有可能的密钥0, 1, 2,…, 25，当尝试到密钥( ? )时，得到明文。

            明文：welcome to shanghai expo

            只要有足够的计算时间和存储容量，原则上穷举法总是可以成功的。但实际中，任何一种能保障安全要求的实用密码都会设计得使这一方法不可行。

它代表什么意思呢？

看过福尔摩斯探案集的人应该会有印象——那是在《跳舞的人，Dancing Men》中出现的“小人密码”。在这个故事里大侦探面对的难题就是要破解这个密码，得到图画中隐含的信息从而获得破案的线索。大侦探接到这张画满小人的纸条当然不可能马上就知道是什么意思。但唯一推测到的是这一串图画代表一串单词或数字。